高中数学北师大版(2019)必修 第一册第二章 函数:综合拔高练(含解析)
文档属性
| 名称 | 高中数学北师大版(2019)必修 第一册第二章 函数:综合拔高练(含解析) | 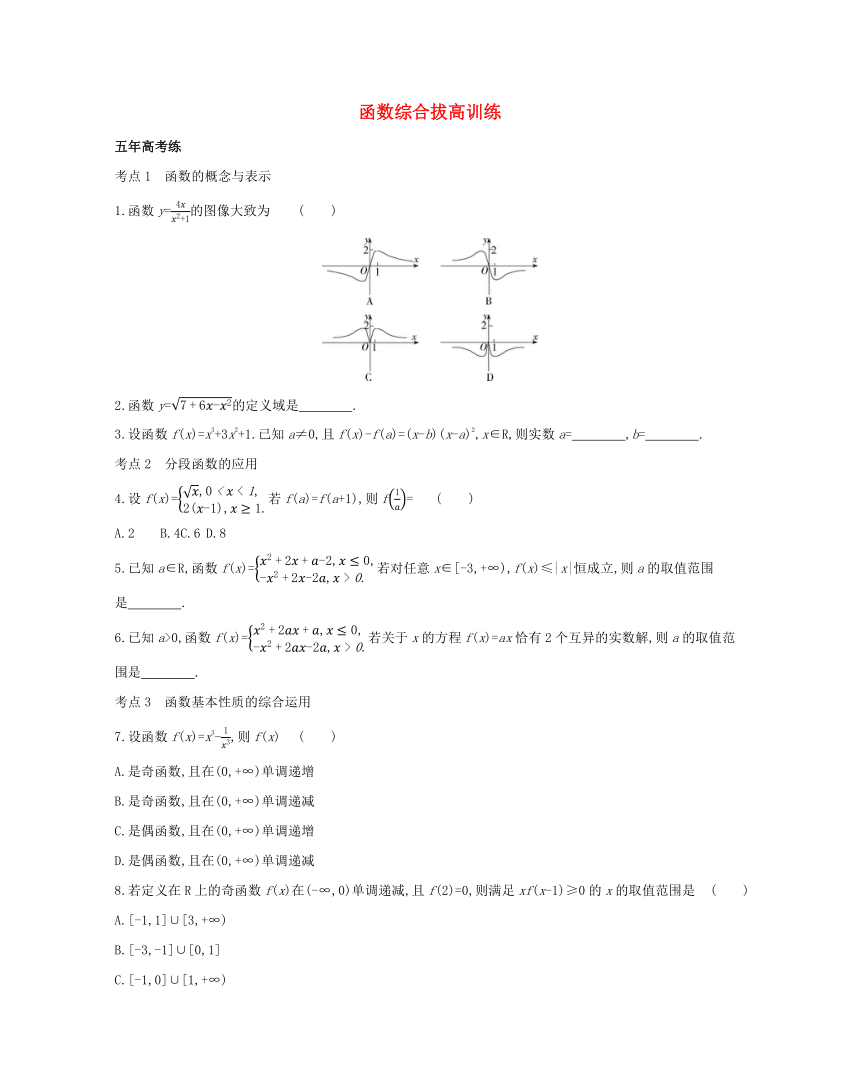 | |
| 格式 | docx | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 13:46:52 | ||
图片预览





文档简介
函数综合拔高训练
五年高考练
考点1 函数的概念与表示
1.函数y=的图像大致为 ( )
2.函数y=的定义域是 .
3.设函数f(x)=x3+3x2+1.已知a≠0,且f(x)-f(a)=(x-b)(x-a)2,x∈R,则实数a= ,b= .
考点2 分段函数的应用
4.设f(x)=若f(a)=f(a+1),则f= ( )
A.2 B.4C.6 D.8
5.已知a∈R,函数f(x)=若对任意x∈[-3,+∞),f(x)≤|x|恒成立,则a的取值范围是 .
6.已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是 .
考点3 函数基本性质的综合运用
7.设函数f(x)=x3-,则f(x) ( )
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
8.若定义在R上的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是 ( )
A.[-1,1]∪[3,+∞)
B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞)
D.[-1,0]∪[1,3]
9.若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m ( )
A.与a有关,且与b有关
B.与a有关,但与b无关
C.与a无关,且与b无关
D.与a无关,但与b有关
10.设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是 ( )
A.
B.
C.
D.
11.已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)= .
12.已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是 .
三年模拟练
1.已知函数f(x)的定义域为[2,8],则函数h(x)=f(2x)+的定义域为 ( )
A.[4,16] B.(-∞,1]∪[3,+∞)
C.[3,4] D.[1,3]
2.已知函数f(x)满足f(x)+2f(1-x)=-1,则f(-2)的值为( )
A.- B.- C. D.
3.若函数y=f(x)的值域为[1,2],则函数f(x)=f(2x+1)-1的值域是 ( )
A.[1,2] B.[0,1] C.[-1,0] D.[2,3]
4.若不等式x2-tx+1<0对一切x∈(1,2)恒成立,则实数t的取值范围为 ( )
A.t<2 B.t> C.t≥1 D.t≥
5.已知定义域为R的函数f(x)在[-2,+∞)上递减,函数y=f(x-2)是偶函数,若f(m+2)A.,5 B.(-1,5)
C.-∞,∪(5,+∞) D.(-∞,-1)∪(5,+∞)
6.已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(其中max{p,q}表示p,q中较大值,min{p,q}表示p,q中较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B= ( )
A.-16 B.16 C.8a D.8a-16
7.函数f(x)=x2+ax-1在[2,3]上不单调,则实数a的取值范围为 .
8.函数y=在区间(-1,+∞)上单调递增,则实数a的取值范围是 .
9.已知函数f(x)=(3m2+5m+3)xm+1是幂函数,对任意x1,x2∈(0,+∞)且x1≠x2有>0,若a,b∈R,a+b<0,则f(a)+f(b) 0(填“>”或“<”).
10.设偶函数f(x)的定义域为(-∞,0)∪(0,+∞),且满足f(1)=1,对于任意x1,x2∈(0,+∞),x1≠x2,都有>0成立,则≥1的解集为 .
11.已知幂函数f(x)=(p2-3p+3)满足f(2)(1)求函数f(x)的解析式;
(2)若函数g(x)=[f(x)]2+mf(x),x∈[1,9],且g(x)的最小值为0,求实数m的值;
(3)若函数h(x)=n-f(x+3),是否存在实数a,b(a12.函数f(x)对定义域D上任意x、y满足:f(x)+f(y)=f(x+y)[1-f(x)f(y)].
(1)求f(0)的值;
(2)设D关于原点对称,试判断f(x)的奇偶性;
(3)设x∈(-a,0)时,f(x)<0,证明f(x)在(0,a)上是增函数.
13.新冠疫情期间,网络直播迅速兴起,某企业看准商机,生产某种直播设备,若每套直播设备的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100套时,每多订购一套,订购的全部直播设备的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500套;
(1)设一次订购量为x套,直播设备的实际出厂单价为P元,求出厂单价P关于一次订购量x的函数;
(2)当销售商一次订购多少套时,该企业获得的利润最大,最大利润是多少元
参考答案:
五年高考练
1.A 4.C 7.A 8.D 9.B
10.B
1.A 设y=f(x)=,易知f(x)的定义域为R,f(-x)==-f(x),∴函数f(x)=是奇函数,∴y=f(x)的图像关于原点对称,排除C、D,易知f(1)=2,排除B,故选A.
2.答案 [-1,7]
解析 要使原函数有意义,需满足7+6x-x2≥0,解得-1≤x≤7,故所求定义域为[-1,7].
3.答案 -2;1
解析 f(x)-f(a)=x3-a3+3(x2-a2)=(x-a)[x2+ax+a2+3(x+a)]=(x-a)[x2+(a+3)·x+a2+3a]=(x-a)(x-a)(x-b),则x2+(a+3)x+a2+3a=x2-(a+b)x+ab,得到解得
4.C 当01,由f(a)=f(a+1),得=2(a+1-1)=2a,解得a=,此时f=f(4)=2×(4-1)=6;当a≥1时,a+1≥2,由f(a)=f(a+1),得2(a-1)=2(a+1-1),此时方程无解.
综上可知,f=6,故选C.
5.答案
解析 当x>0时,f(x)=-x2+2x-2a,
此时只需-x2+2x-2a≤x恒成立,
即2a≥-x2+x恒成立.
因为x>0时,-x2+x的最大值为,
所以a≥;
当-3≤x≤0时,f(x)=x2+2x+a-2,
此时只需x2+2x+a-2≤-x恒成立,
即a≤-x2-3x+2恒成立,
因为-3≤x≤0时,-x2-3x+2的最小值为2,
所以a≤2.故a的取值范围为.
6.答案 (4,8)
解析 当x≤0时,方程f(x)=ax,即x2+ax+a=0①;当x>0时,方程f(x)=ax,即x2-ax+2a=0②.因为a>0,所以由根与系数的关系可知方程①②均不可能有异号实根,故方程f(x)=ax有2个互异实根只能是:方程①有两个不同负实根且方程②无正实根;或者方程①无负实根且方程②有两个不同正实根.
方程①有两个不同负实根,只要Δ=a2-4a>0,即a>4即可,方程②无正实根,只要Δ=a2-8a<0,即a<8即可,此时4同理,方程①无负实根且方程②有两个不同正实根,只需a<4且a>8,此时无解.
综上可知,实数a的取值范围是(4,8).
7.A ∵f(x)=x3-定义域为{x|x≠0},其关于原点对称,而f(-x)=-f(x),
∴f(x)为奇函数,又∵y=x3在(0,+x3)上单调递增,在(-∞,0)上单调递增,而y==x-3在(0,+∞)上单调递减,在(-∞,0)上单调递减,∴函数f(x)=x3-在(0,+∞)上单调递增,在(-∞,0)上单调递增.故选A.
8.D ∵f(x)是定义在R上的奇函数,∴f(x-1)的图像关于点(1,0)中心对称,又∵f(x)在(-∞,0)上单调递减,∴f(x-1)在(-∞,1)上单调递减,在(1,+∞)上也单调递减,且过(-1,0)和(3,0),f(x-1)的大致图像如图:
当-1≤x≤0时,f(x-1)≤0,
∴xf(x-1)≥0;当1≤x≤3时,f(x-1)≥0,
∴xf(x-1)≥0.
综上,满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].故选D.
9.B 由题意,得f(x)=x2+ax+b=+b-,因此函数f(x)的图像的对称轴为直线x=-.当-≤0,即a≥0时,函数f(x)在区间[0,1]上单调递增,所以函数f(x)的最大值M=f(1)=1+a+b,最小值m=f(0)=b,所以M-m=1+a;当-≥1,即a≤-2时,函数f(x)在区间[0,1]上单调递减,所以函数f(x)的最大值M=f(0)=b,最小值m=f(1)=1+a+b,所以M-m=-1-a;当0<-≤,即-1≤a<0时,函数f(x)在[0,1]上的最小值m=f=b-,最大值M=f(1)=1+a+b,所以M-m=1+a+;当<-<1,即-210.B 由题意可知,当x∈(0,1]时,f(x)=x(x-1)=x2-x,则当x=时,f(x)min=-,且当x=时,f(x)=-.当x∈(1,2]时,x-1∈(0,1],则f(x)=2f(x-1).当x∈(-1,0]时,x+1∈(0,1],则 f(x)=f(x+1).
∴若x∈(1,2],则当x=时,f(x)min=-,且x=时,f(x)=-.
同理,若x∈(2,3],则当x=时,f(x)min=-1,且x=时,f(x)=-.
∴函数f(x)的大致图像如图所示.
∵f(x)≥-对任意x∈(-∞,m]恒成立,∴当x∈(-∞,m]时,f(x)min≥-,由图可知m≤.故选B.
11.答案 12
解析 因为函数f(x)为奇函数,所以f(2)=-f(-2)=-[2×(-2)3+(-2)2]=12.
12.答案
解析 由x+y=1,得y=1-x,所以x2+y2=x2+(1-x)2=2x2-2x+1.由x≥0,y≥0,x+y=1,得0≤x≤1.令f(x)=2x2-2x+1,由二次函数的图像(图略)可知,当x=时,f(x)=2x2-2x+1取得最小值,即x2+y2的最小值为;当x=0或x=1时,f(x)=2x2-2x+1取得最大值1,即x2+y2的最大值为1.故x2+y2的取值范围是.
三年模拟练
1.D 2.C 3.B 4.D 5.B
6.A
1.D 由题意得解得1≤x≤3,故h(x)的定义域为[1,3].故选D.
2.C 依题意,取x=-2,得f(-2)+2f(3)=-,①
取x=3,得f(3)+2f(-2)=-,②
联立①②得f(-2)=,故选C.
3.B 因为y=f(x)的值域是[1,2],而y=f(2x+1)与函数y=f(x)定义域不同,值域相同,
所以y=f(2x+1)的值域是[1,2],所以f(x)=f(2x+1)-1的值域为[0,1].故选B.
4.D 因为不等式x2-tx+1<0对一切x∈(1,2)恒成立,所以t>=x+在区间(1,2)上恒成立,令y=x+,
由对勾函数的性质可知函数y=x+在区间(1,2)上单调递增,且当x=2时,ymax=2+=,所以实数t的取值范围是t≥.故选D.
5.B 因为函数y=f(x-2)是偶函数,所以y=f(x)的图像关于直线x=-2对称,
又因为f(x)在[-2,+∞)上递减,所以f(x)在(-∞,-2]上递增,所以函数图像上的点离对称轴越近其纵坐标越大.
若f(m+2)所以(2m-1)2<(m+4)2,即m2-4m-5<0,
解得-16.A 由题意,得f(x)=(x-a-2)2-4a-4,
g(x)=-(x-a+2)2-4a+12,
当x=a+2时,f(x)=g(x)=-4a-4;
当x=a-2时,f(x)=g(x)=-4a+12.
因为g(x)max=-4a+12,所以H2(x)≤g(x)≤g(x)max=-4a+12.
因为f(x)min=-4a-4,所以H1(x)≥f(x)≥f(x)min=-4a-4,
所以A=-4a-4,B=-4a+12,所以A-B=-16,故选A.
7.答案 (-6,-4)
解析 由题知,函数f(x)的图像的对称轴为直线x=-.
∵f(x)在[2,3]上不单调,∴2<-<3,解得-68.答案 (-∞,-3]
解析 y===1+.因为函数y=在区间(-1,+∞)上单调递增,所以解得a≤-3,所以实数a的取值范围是(-∞,-3].
9.答案 <
解析 ∵f(x)=(3m2+5m+3)xm+1是幂函数,∴3m2+5m+3=1,
解得m=-或m=-1.
当m=-时,f(x)=,当m=-1时,f(x)=x0=1,又∵对任意x1,x2∈(0,+∞)且x1≠x2有>0,
∴f(x)在(0,+∞)上单调递增,∴f(x)=,易知f(x)的定义域为R,且f(-x)=f(-x=-=-f(x),
∴f(x)为R上的奇函数.∵a+b<0,
∴a<-b,∴f(a)∴f(a)+f(b)<0.
10.答案 (-∞,-1]∪[1,+∞)
解析 令g(x)=,则
==.
因为>0对于任意x1,x2∈(0,+∞),x1≠x2恒成立,>0,
所以>0对任意x1,x2∈(0,+∞),x1≠x2恒成立,所以g(x)=在(0,+∞)上单调递增.
因为f(x)是偶函数,所以g(x)=也是偶函数,不等式≥1=等价于g(x)≥g(1),所以|x|≥1,
解得x≥1或x≤-1,所以≥1的解集为(-∞,-1]∪[1,+∞).
11.解析 (1)∵f(x)为幂函数,
∴p2-3p+3=1,解得p=1或p=2.
当p=1时,f(x)=x-1在(0,+∞)上单调递减,故f(2)>f(4),不符合题意,舍去;
当p=2时,f(x)==在(0,+∞)上单调递增,
故f(2)∴f(x)=.
(2)由(1),知g(x)=x+m,
令t=,∵x∈[1,9],∴t∈[1,3],
∴g(t)=t2+mt,t∈[1,3].
①当-≤1,即m≥-2时,函数g(t)在[1,3]上单调递增,∴当t=1时,g(t)有最小值,∴1+m=0,∴m=-1;
②当1<-<3,即-6∴-=0,∴m=0(舍);
③当-≥3,即m≤-6时,函数g(t)在[1,3]上单调递减,∴当t=3时,g(t)有最小值,∴9+3m=0,∴m=-3(舍).
综上所述,m=-1.
(3)由(1),知h(x)=n-,易知h(x)在[-3,+∞)上单调递减,
∴即
②-①,得-=a-b=a+3-(b+3),
又(a+3)-(b+3)=(-)·(+),∴+=1,
故有n=a+=a+1-.
∵a≥-3且a∴a令s=,∴0≤s<,
∴n=a+1-=s2-s-2=s-2-,0≤s<,
∴-故实数n的取值范围是.
12.解析 (1)令x=y=0,
∴f(0)+f(0)=f(0)[1-f2(0)],
∴2f(0)=f(0)-f3(0),
∴f3(0)+f(0)=0,
∴f(0)=0.
(2)由题意知,定义域D关于原点对称,
令y=-x,
∴f(x)+f(-x)=f(0)[1-f(x)f(-x)],
∴f(x)+f(-x)=0,
即f(x)=-f(-x)对定义域D内的任意实数都成立,
∴f(x)是定义域D内的奇函数.
(3)证明:设0∴f(x1)-f(x2)=f(x1)+f(-x2)
=f(x1-x2)[1-f(x1)f(-x2)]
=f(x1-x2)[1+f(-x1)f(-x2)],
又∵-a∴f(x1-x2)<0,f(-x1)<0,f(-x2)<0,
∴f(x1-x2)[1+f(-x1)f(-x2)]<0,
即f(x1)-f(x2)<0,
∴f(x)在(0,a)上是增函数.
13.信息提取 ①每个直播设备的成本为40元,出厂单价定为60元;②订购量超过100套时,每多订购一套,订购的全部直播设备的出厂单价就降低0.02元;③销售商一次订购量不会超过500套.
数学建模 本题以社会热点问题为背景,构建函数模型,利用函数思想求得函数的解析式及最值,从而解决实际问题中的最优化问题.
解析 (1)当0当100所以P=
(2)设销售商一次订购x套时,该企业获得的利润为L元,
则L=
当0当100∵6000>2000,∴当销售商一次订购500套时,该企业获得的利润最大,最大利润是6000元.
解题模板
构建函数模型解决实际生活中的最优化问题的步骤:(1)认真审题;(2)挖掘题中的等量关系,构建函数模型;(3)利用函数的性质(尤其是单调性)求得该函数的最值;(4)将数学问题中的解还原成实际问题的解.
五年高考练
考点1 函数的概念与表示
1.函数y=的图像大致为 ( )
2.函数y=的定义域是 .
3.设函数f(x)=x3+3x2+1.已知a≠0,且f(x)-f(a)=(x-b)(x-a)2,x∈R,则实数a= ,b= .
考点2 分段函数的应用
4.设f(x)=若f(a)=f(a+1),则f= ( )
A.2 B.4C.6 D.8
5.已知a∈R,函数f(x)=若对任意x∈[-3,+∞),f(x)≤|x|恒成立,则a的取值范围是 .
6.已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是 .
考点3 函数基本性质的综合运用
7.设函数f(x)=x3-,则f(x) ( )
A.是奇函数,且在(0,+∞)单调递增
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
8.若定义在R上的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是 ( )
A.[-1,1]∪[3,+∞)
B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞)
D.[-1,0]∪[1,3]
9.若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m ( )
A.与a有关,且与b有关
B.与a有关,但与b无关
C.与a无关,且与b无关
D.与a无关,但与b有关
10.设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是 ( )
A.
B.
C.
D.
11.已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)= .
12.已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是 .
三年模拟练
1.已知函数f(x)的定义域为[2,8],则函数h(x)=f(2x)+的定义域为 ( )
A.[4,16] B.(-∞,1]∪[3,+∞)
C.[3,4] D.[1,3]
2.已知函数f(x)满足f(x)+2f(1-x)=-1,则f(-2)的值为( )
A.- B.- C. D.
3.若函数y=f(x)的值域为[1,2],则函数f(x)=f(2x+1)-1的值域是 ( )
A.[1,2] B.[0,1] C.[-1,0] D.[2,3]
4.若不等式x2-tx+1<0对一切x∈(1,2)恒成立,则实数t的取值范围为 ( )
A.t<2 B.t> C.t≥1 D.t≥
5.已知定义域为R的函数f(x)在[-2,+∞)上递减,函数y=f(x-2)是偶函数,若f(m+2)
C.-∞,∪(5,+∞) D.(-∞,-1)∪(5,+∞)
6.已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(其中max{p,q}表示p,q中较大值,min{p,q}表示p,q中较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B= ( )
A.-16 B.16 C.8a D.8a-16
7.函数f(x)=x2+ax-1在[2,3]上不单调,则实数a的取值范围为 .
8.函数y=在区间(-1,+∞)上单调递增,则实数a的取值范围是 .
9.已知函数f(x)=(3m2+5m+3)xm+1是幂函数,对任意x1,x2∈(0,+∞)且x1≠x2有>0,若a,b∈R,a+b<0,则f(a)+f(b) 0(填“>”或“<”).
10.设偶函数f(x)的定义域为(-∞,0)∪(0,+∞),且满足f(1)=1,对于任意x1,x2∈(0,+∞),x1≠x2,都有>0成立,则≥1的解集为 .
11.已知幂函数f(x)=(p2-3p+3)满足f(2)
(2)若函数g(x)=[f(x)]2+mf(x),x∈[1,9],且g(x)的最小值为0,求实数m的值;
(3)若函数h(x)=n-f(x+3),是否存在实数a,b(a
(1)求f(0)的值;
(2)设D关于原点对称,试判断f(x)的奇偶性;
(3)设x∈(-a,0)时,f(x)<0,证明f(x)在(0,a)上是增函数.
13.新冠疫情期间,网络直播迅速兴起,某企业看准商机,生产某种直播设备,若每套直播设备的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100套时,每多订购一套,订购的全部直播设备的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500套;
(1)设一次订购量为x套,直播设备的实际出厂单价为P元,求出厂单价P关于一次订购量x的函数;
(2)当销售商一次订购多少套时,该企业获得的利润最大,最大利润是多少元
参考答案:
五年高考练
1.A 4.C 7.A 8.D 9.B
10.B
1.A 设y=f(x)=,易知f(x)的定义域为R,f(-x)==-f(x),∴函数f(x)=是奇函数,∴y=f(x)的图像关于原点对称,排除C、D,易知f(1)=2,排除B,故选A.
2.答案 [-1,7]
解析 要使原函数有意义,需满足7+6x-x2≥0,解得-1≤x≤7,故所求定义域为[-1,7].
3.答案 -2;1
解析 f(x)-f(a)=x3-a3+3(x2-a2)=(x-a)[x2+ax+a2+3(x+a)]=(x-a)[x2+(a+3)·x+a2+3a]=(x-a)(x-a)(x-b),则x2+(a+3)x+a2+3a=x2-(a+b)x+ab,得到解得
4.C 当0
综上可知,f=6,故选C.
5.答案
解析 当x>0时,f(x)=-x2+2x-2a,
此时只需-x2+2x-2a≤x恒成立,
即2a≥-x2+x恒成立.
因为x>0时,-x2+x的最大值为,
所以a≥;
当-3≤x≤0时,f(x)=x2+2x+a-2,
此时只需x2+2x+a-2≤-x恒成立,
即a≤-x2-3x+2恒成立,
因为-3≤x≤0时,-x2-3x+2的最小值为2,
所以a≤2.故a的取值范围为.
6.答案 (4,8)
解析 当x≤0时,方程f(x)=ax,即x2+ax+a=0①;当x>0时,方程f(x)=ax,即x2-ax+2a=0②.因为a>0,所以由根与系数的关系可知方程①②均不可能有异号实根,故方程f(x)=ax有2个互异实根只能是:方程①有两个不同负实根且方程②无正实根;或者方程①无负实根且方程②有两个不同正实根.
方程①有两个不同负实根,只要Δ=a2-4a>0,即a>4即可,方程②无正实根,只要Δ=a2-8a<0,即a<8即可,此时4
综上可知,实数a的取值范围是(4,8).
7.A ∵f(x)=x3-定义域为{x|x≠0},其关于原点对称,而f(-x)=-f(x),
∴f(x)为奇函数,又∵y=x3在(0,+x3)上单调递增,在(-∞,0)上单调递增,而y==x-3在(0,+∞)上单调递减,在(-∞,0)上单调递减,∴函数f(x)=x3-在(0,+∞)上单调递增,在(-∞,0)上单调递增.故选A.
8.D ∵f(x)是定义在R上的奇函数,∴f(x-1)的图像关于点(1,0)中心对称,又∵f(x)在(-∞,0)上单调递减,∴f(x-1)在(-∞,1)上单调递减,在(1,+∞)上也单调递减,且过(-1,0)和(3,0),f(x-1)的大致图像如图:
当-1≤x≤0时,f(x-1)≤0,
∴xf(x-1)≥0;当1≤x≤3时,f(x-1)≥0,
∴xf(x-1)≥0.
综上,满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].故选D.
9.B 由题意,得f(x)=x2+ax+b=+b-,因此函数f(x)的图像的对称轴为直线x=-.当-≤0,即a≥0时,函数f(x)在区间[0,1]上单调递增,所以函数f(x)的最大值M=f(1)=1+a+b,最小值m=f(0)=b,所以M-m=1+a;当-≥1,即a≤-2时,函数f(x)在区间[0,1]上单调递减,所以函数f(x)的最大值M=f(0)=b,最小值m=f(1)=1+a+b,所以M-m=-1-a;当0<-≤,即-1≤a<0时,函数f(x)在[0,1]上的最小值m=f=b-,最大值M=f(1)=1+a+b,所以M-m=1+a+;当<-<1,即-2
∴若x∈(1,2],则当x=时,f(x)min=-,且x=时,f(x)=-.
同理,若x∈(2,3],则当x=时,f(x)min=-1,且x=时,f(x)=-.
∴函数f(x)的大致图像如图所示.
∵f(x)≥-对任意x∈(-∞,m]恒成立,∴当x∈(-∞,m]时,f(x)min≥-,由图可知m≤.故选B.
11.答案 12
解析 因为函数f(x)为奇函数,所以f(2)=-f(-2)=-[2×(-2)3+(-2)2]=12.
12.答案
解析 由x+y=1,得y=1-x,所以x2+y2=x2+(1-x)2=2x2-2x+1.由x≥0,y≥0,x+y=1,得0≤x≤1.令f(x)=2x2-2x+1,由二次函数的图像(图略)可知,当x=时,f(x)=2x2-2x+1取得最小值,即x2+y2的最小值为;当x=0或x=1时,f(x)=2x2-2x+1取得最大值1,即x2+y2的最大值为1.故x2+y2的取值范围是.
三年模拟练
1.D 2.C 3.B 4.D 5.B
6.A
1.D 由题意得解得1≤x≤3,故h(x)的定义域为[1,3].故选D.
2.C 依题意,取x=-2,得f(-2)+2f(3)=-,①
取x=3,得f(3)+2f(-2)=-,②
联立①②得f(-2)=,故选C.
3.B 因为y=f(x)的值域是[1,2],而y=f(2x+1)与函数y=f(x)定义域不同,值域相同,
所以y=f(2x+1)的值域是[1,2],所以f(x)=f(2x+1)-1的值域为[0,1].故选B.
4.D 因为不等式x2-tx+1<0对一切x∈(1,2)恒成立,所以t>=x+在区间(1,2)上恒成立,令y=x+,
由对勾函数的性质可知函数y=x+在区间(1,2)上单调递增,且当x=2时,ymax=2+=,所以实数t的取值范围是t≥.故选D.
5.B 因为函数y=f(x-2)是偶函数,所以y=f(x)的图像关于直线x=-2对称,
又因为f(x)在[-2,+∞)上递减,所以f(x)在(-∞,-2]上递增,所以函数图像上的点离对称轴越近其纵坐标越大.
若f(m+2)
解得-1
g(x)=-(x-a+2)2-4a+12,
当x=a+2时,f(x)=g(x)=-4a-4;
当x=a-2时,f(x)=g(x)=-4a+12.
因为g(x)max=-4a+12,所以H2(x)≤g(x)≤g(x)max=-4a+12.
因为f(x)min=-4a-4,所以H1(x)≥f(x)≥f(x)min=-4a-4,
所以A=-4a-4,B=-4a+12,所以A-B=-16,故选A.
7.答案 (-6,-4)
解析 由题知,函数f(x)的图像的对称轴为直线x=-.
∵f(x)在[2,3]上不单调,∴2<-<3,解得-6
解析 y===1+.因为函数y=在区间(-1,+∞)上单调递增,所以解得a≤-3,所以实数a的取值范围是(-∞,-3].
9.答案 <
解析 ∵f(x)=(3m2+5m+3)xm+1是幂函数,∴3m2+5m+3=1,
解得m=-或m=-1.
当m=-时,f(x)=,当m=-1时,f(x)=x0=1,又∵对任意x1,x2∈(0,+∞)且x1≠x2有>0,
∴f(x)在(0,+∞)上单调递增,∴f(x)=,易知f(x)的定义域为R,且f(-x)=f(-x=-=-f(x),
∴f(x)为R上的奇函数.∵a+b<0,
∴a<-b,∴f(a)
10.答案 (-∞,-1]∪[1,+∞)
解析 令g(x)=,则
==.
因为>0对于任意x1,x2∈(0,+∞),x1≠x2恒成立,>0,
所以>0对任意x1,x2∈(0,+∞),x1≠x2恒成立,所以g(x)=在(0,+∞)上单调递增.
因为f(x)是偶函数,所以g(x)=也是偶函数,不等式≥1=等价于g(x)≥g(1),所以|x|≥1,
解得x≥1或x≤-1,所以≥1的解集为(-∞,-1]∪[1,+∞).
11.解析 (1)∵f(x)为幂函数,
∴p2-3p+3=1,解得p=1或p=2.
当p=1时,f(x)=x-1在(0,+∞)上单调递减,故f(2)>f(4),不符合题意,舍去;
当p=2时,f(x)==在(0,+∞)上单调递增,
故f(2)
(2)由(1),知g(x)=x+m,
令t=,∵x∈[1,9],∴t∈[1,3],
∴g(t)=t2+mt,t∈[1,3].
①当-≤1,即m≥-2时,函数g(t)在[1,3]上单调递增,∴当t=1时,g(t)有最小值,∴1+m=0,∴m=-1;
②当1<-<3,即-6
③当-≥3,即m≤-6时,函数g(t)在[1,3]上单调递减,∴当t=3时,g(t)有最小值,∴9+3m=0,∴m=-3(舍).
综上所述,m=-1.
(3)由(1),知h(x)=n-,易知h(x)在[-3,+∞)上单调递减,
∴即
②-①,得-=a-b=a+3-(b+3),
又(a+3)-(b+3)=(-)·(+),∴+=1,
故有n=a+=a+1-.
∵a≥-3且a
∴n=a+1-=s2-s-2=s-2-,0≤s<,
∴-
12.解析 (1)令x=y=0,
∴f(0)+f(0)=f(0)[1-f2(0)],
∴2f(0)=f(0)-f3(0),
∴f3(0)+f(0)=0,
∴f(0)=0.
(2)由题意知,定义域D关于原点对称,
令y=-x,
∴f(x)+f(-x)=f(0)[1-f(x)f(-x)],
∴f(x)+f(-x)=0,
即f(x)=-f(-x)对定义域D内的任意实数都成立,
∴f(x)是定义域D内的奇函数.
(3)证明:设0
=f(x1-x2)[1-f(x1)f(-x2)]
=f(x1-x2)[1+f(-x1)f(-x2)],
又∵-a
∴f(x1-x2)[1+f(-x1)f(-x2)]<0,
即f(x1)-f(x2)<0,
∴f(x)在(0,a)上是增函数.
13.信息提取 ①每个直播设备的成本为40元,出厂单价定为60元;②订购量超过100套时,每多订购一套,订购的全部直播设备的出厂单价就降低0.02元;③销售商一次订购量不会超过500套.
数学建模 本题以社会热点问题为背景,构建函数模型,利用函数思想求得函数的解析式及最值,从而解决实际问题中的最优化问题.
解析 (1)当0
(2)设销售商一次订购x套时,该企业获得的利润为L元,
则L=
当0
解题模板
构建函数模型解决实际生活中的最优化问题的步骤:(1)认真审题;(2)挖掘题中的等量关系,构建函数模型;(3)利用函数的性质(尤其是单调性)求得该函数的最值;(4)将数学问题中的解还原成实际问题的解.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
