第五单元平行四边形和梯形易错点检测卷(单元测试)数学四年级上册人教版 (含答案)
文档属性
| 名称 | 第五单元平行四边形和梯形易错点检测卷(单元测试)数学四年级上册人教版 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 951.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 21:54:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五单元平行四边形和梯形易错点检测卷(单元测试)-小学数学四年级上册人教版
一、选择题
1.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是( )。
A.互相平行 B.互相垂直 C.无法确定
2.从下面的集合图中可以看出,正方形、长方形、平行四边形和梯形都属于( )。
A.四边形 B.平行四边形 C.长方形
3.上午9时整,钟面上的时针和分针( )。
A.互相垂直 B.互相平行 C.重合
4.下图中一个端点是A的最短线段是( )。
A.AB B.AC C.AD D.AE
5.下面说法错误的是( )。
A.人们将圆分成360等份,把其中1份所对的角作为度量角的单位。
B.把一个长方形框架拉成一个平行四边形,周长不变。
C.从平行四边形的一个顶点出发只能画出一条高。
D.两组对边分别平行且相等的四边形一定是平行四边形。
二、填空题
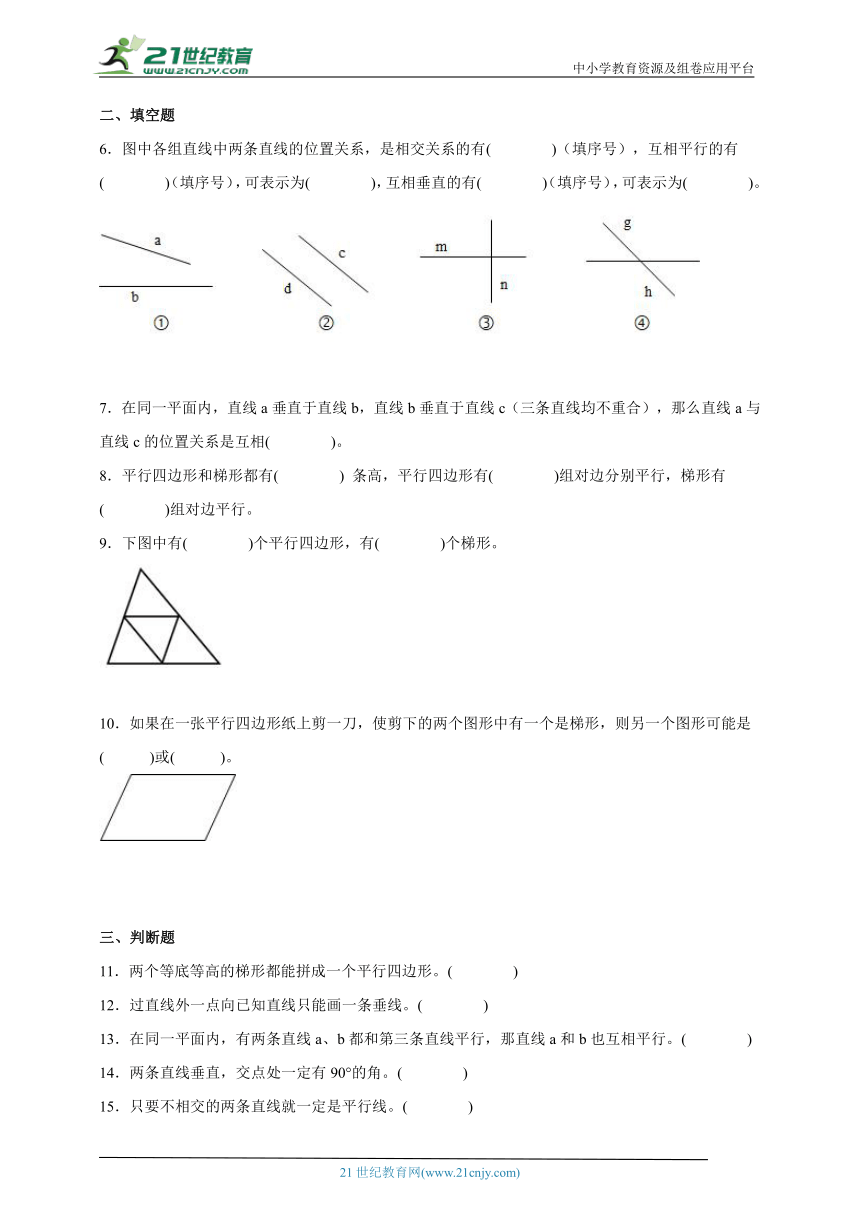
6.图中各组直线中两条直线的位置关系,是相交关系的有( )(填序号),互相平行的有( )(填序号),可表示为( ),互相垂直的有( )(填序号),可表示为( )。
7.在同一平面内,直线a垂直于直线b,直线b垂直于直线c(三条直线均不重合),那么直线a与直线c的位置关系是互相( )。
8.平行四边形和梯形都有( ) 条高,平行四边形有( )组对边分别平行,梯形有( )组对边平行。
9.下图中有( )个平行四边形,有( )个梯形。
10.如果在一张平行四边形纸上剪一刀,使剪下的两个图形中有一个是梯形,则另一个图形可能是( )或( )。
三、判断题
11.两个等底等高的梯形都能拼成一个平行四边形。( )
12.过直线外一点向已知直线只能画一条垂线。( )
13.在同一平面内,有两条直线a、b都和第三条直线平行,那直线a和b也互相平行。( )
14.两条直线垂直,交点处一定有90°的角。( )
15.只要不相交的两条直线就一定是平行线。( )
四、解答题
16.把下面的图补成一个长方形,量出必须的数据(精确到整厘米数),并计算出这个长方形的面积。
17.要从幸福小区向小河挖一条通水管道,要使管道最短,应该怎样挖?请你在图上画出来。
18.如下图,小熊在A点,小羚羊在B点,它们渴极了,都要到河边喝水,为了让它们尽快喝到水,请你为它们设计出到河边的最短路线,在图上画出来,并说明理由。
19.在正方形ABCD中,哪些线段互相垂直?
20.
(1)量一量,图中∠1是( )度,这是一个( )角。
(2)如果上面方格图中给定的线段AC是等腰梯形的一条腰,AB为这个等腰梯形的上底,请把这个等腰梯形画完整。
(3)画出这个等腰梯形的一条高。
参考答案:
1.A
【分析】根据垂直的性质:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行,也可以根据题目作图帮助解答。
【详解】
图中直线b和直线c都是垂直与直线a的,可以看出直线b和直线c互相平行。
故答案为:A
【点睛】本题考查在同一平面内两条直线的位置判定,应熟练掌握平行和垂直的概念及性质并灵活运用。
2.A
【分析】四边形就是四条线段围成的图形,有四条边,四个角,据此解答。
【详解】正方形、长方形、平行四边形和梯形都具有四边形的特征,属于四边形。
故答案为:A
【点睛】本题主要考查了四边形的特征。
3.A
【分析】钟面上一大格是90°。9点钟时,钟表的时针指向数字9,分针指向12,时针和分针之间有3个大格,是90度,即时针和分针互相垂直,据此解答即可。
【详解】上午9时,钟面上的时针和分针互相垂直;
故选:A。
【点睛】本题考查了角的度量,以及钟面上的角,关键要知道钟面一周平均分60格,钟面上每一大格的度数为360°÷12=30°。
4.C
【分析】先判断哪个是垂线段,再根据点到直线的距离,垂线段最短,即可解答。
【详解】由图可知AD是点A到BC的垂线段,根据点到直线的距离,垂线段最短可知AD最短。
所以答案为:C
【点睛】点到直线的距离垂线段最短。
5.C
【分析】根据度量角的定义和长方形以及平行四边形的特征判断分析即可。
【详解】A.将圆平均分成360份,其中一份所对的角作为度量角的单位,是正确的;
B.把一个长方形框架拉成一个平行四边形,四条边的长度都没变,所以周长不变,是正确的;
C.从平行四边形的一个顶点出发可以画出两条高;故此选项错误;
D.两组对边平行且相等的四边形一定是平行四边形,是正确的。
所以答案为:C
【点睛】本题为综合题 ,掌握度量角的知识和长方形和平行四边形的特征是解题的关键。
6. ①③④ ② d∥c ③ m⊥n
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足,垂直用“⊥”表示。同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线,平行用“//”表示。在同一平面内的两条直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
【详解】图中各组直线中两条直线的位置关系,是相交关系的有①③④ (填序号),互相平行的有②(填序号),可表示为d∥c,互相垂直的有③(填序号),可表示为m⊥n。
【点睛】本题主要考查学生对相交、垂直和平行概念的掌握和灵活运用。
7.平行
【分析】
根据垂直和平行的性质可知,同一平面内,a⊥b,b⊥c,则a∥c。即同一平面内,垂直于同一条直线的两条直线互相平行。
【详解】在同一平面内,直线a垂直于直线b,直线b垂直于直线c(三条直线均不重合),那么直线a与直线c的位置关系是互相平行。
【点睛】熟练掌握平行和垂直的定义是解决本题的关键,画图能帮助学生更好的理解。
8. 无数 两 一
【分析】
从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。则平行四边形和梯形均有无数条高。平行四边形有两组对边平行,而梯形只有一组对边平行。据此解答。
【详解】平行四边形和梯形都有无数 条高,平行四边形有两组对边分别平行,梯形有一组对边平行。
【点睛】本题考查平行四边形和梯形的性质,平行四边形有两组高,无数条高。梯形有一组高,无数条高。
9. 3 3
【分析】两组对边分别平行的四边形,叫做平行四边形;只有一组对边平行的四边形叫做梯形;依此计算出它们的个数即可。
【详解】1+1+1=3(个),即图中有3个平行四边形;
1+1+1=3(个),即图中有3个梯形。
【点睛】熟练掌握梯形和平行四边形的特点是解答此题的关键。
10. 梯形 三角形
【分析】在一张平行四边形纸片上剪一刀可能变成:①一个三角形和一个梯形;②两个三角形;③两个平行四边形;④两个梯形,由此求解。
【详解】如果在一张平行四边形纸上剪一刀,使剪下的两个图形中有一个是梯形,则另一个图形可能是梯形或三角形。
【点睛】本题考查学生的动手操作能力,可以在练习本上画一画可能的情况。
11.×
【分析】两个完全一样的梯形能拼成一个平行四边形,等底等高的梯形并不一定会是完全一样的,据此分析。
【详解】如图,两个梯形等底等高,不一定能拼成一个平行四边形。
故答案为:×
【点睛】关键是熟悉平行四边形特征,注意“完全一样”的梯形才可以拼成平行四边形,不是等底等高。
12.√
【分析】连接直线外一点与直线各点的所有线段中,垂线段最短,据此解答。
【详解】过直线外一点向已知直线画垂线,只能画一条。
故答案为:√
【点睛】熟练掌握垂线段的定义并灵活应用是解答此题的关键。
13.√
【分析】利用平行公理的推论直接作答。
【详解】平行的推论:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也平行。
故答案为:√
【点睛】理解和掌握平行的推论,是解答此题的关键所在。
14.√
【分析】根据垂直的定义:同一平面内,两条直线相交,组成的四个角中,有一个角是直角,这两条直线就互相垂直。
【详解】两条直线垂直,交点处一定有90°的角。
故答案为:√
【点睛】熟练掌握垂直的定义是解答此题的关键。
15.×
【详解】在同一平面内,永不相交的两条直线叫做平行线。如下图所示:
故答案为:×
16.见详解
【分析】长方形的两组对边分别互相平行,两组对边分别相等,四个角都是直角;
根据测量长度的方法量出长方形的长和宽,并根据长方形的特点把此图补成一个长方形,长方形的面积=长×宽,依此计算出长方形的面积即可。
【详解】
面积为:3×5=15(平方厘米)
答:这个长方形的面积是15平方厘米。
【点睛】此题考查的是长方形的特点,以及长方形的面积的计算,应熟练掌握。
17.从幸福小区到小河作垂线段;画图见详解
【分析】根据从直线外一点到这条直线所画的垂直线段最短,要从幸福小区向小河挖一条通水管道,要使管道最短,就要从幸福小区到小河作垂线段。
【详解】要使管道最短,就要从幸福小区到小河作垂线段;画图如下:
【点睛】本题考查了学生对垂线段最短的掌握情况,同时检查了学生的作图能力,及利用数学知识解决实际问题的能力。注意垂线段最短。
18.图见详解;从直线外一点到这条直线的线段中,垂直线段最短
【分析】过直线上或直线外一点作垂线的步骤:
1、把三角尺的一条直角边与已知直线重合。
2、沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。
3、沿三角尺的另一条直角边画一条直线,并画上垂直符号。
这条直线就是已知直线的垂线。
过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
【详解】作图如下:
理由:从直线外一点到这条直线的线段中,垂直线段最短
【点睛】过直线外一点,画已知直线的平行线可以借助直尺和三角尺来完成。
19.见详解
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。据此解答即可。
【详解】AB⊥BC;AB⊥AD;CD⊥AD;CD⊥BC;AC⊥BD
【点睛】本题考查垂直的性质,要判断哪两条线段互相垂直,就看哪两条线段的夹角是直角。
20.(1)130;钝;
(2)(3)见详解
【分析】(1)用量角器测量出∠1的度数,并根据度数判断这是一个什么角。
(2)过点C向右画10个格长的线段,并且平行于线段AB,连接B点与刚画线段的另一个端点所成的图形就是等腰梯形。
(3)梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线,用三角板的直角可以画出梯形的一条高。
【详解】(1)量一量,图中∠1是(130)度,这是一个(钝)角。
(2)(3)
【点睛】熟悉等腰梯形的特征是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元平行四边形和梯形易错点检测卷(单元测试)-小学数学四年级上册人教版
一、选择题
1.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是( )。
A.互相平行 B.互相垂直 C.无法确定
2.从下面的集合图中可以看出,正方形、长方形、平行四边形和梯形都属于( )。
A.四边形 B.平行四边形 C.长方形
3.上午9时整,钟面上的时针和分针( )。
A.互相垂直 B.互相平行 C.重合
4.下图中一个端点是A的最短线段是( )。
A.AB B.AC C.AD D.AE
5.下面说法错误的是( )。
A.人们将圆分成360等份,把其中1份所对的角作为度量角的单位。
B.把一个长方形框架拉成一个平行四边形,周长不变。
C.从平行四边形的一个顶点出发只能画出一条高。
D.两组对边分别平行且相等的四边形一定是平行四边形。
二、填空题
6.图中各组直线中两条直线的位置关系,是相交关系的有( )(填序号),互相平行的有( )(填序号),可表示为( ),互相垂直的有( )(填序号),可表示为( )。
7.在同一平面内,直线a垂直于直线b,直线b垂直于直线c(三条直线均不重合),那么直线a与直线c的位置关系是互相( )。
8.平行四边形和梯形都有( ) 条高,平行四边形有( )组对边分别平行,梯形有( )组对边平行。
9.下图中有( )个平行四边形,有( )个梯形。
10.如果在一张平行四边形纸上剪一刀,使剪下的两个图形中有一个是梯形,则另一个图形可能是( )或( )。
三、判断题
11.两个等底等高的梯形都能拼成一个平行四边形。( )
12.过直线外一点向已知直线只能画一条垂线。( )
13.在同一平面内,有两条直线a、b都和第三条直线平行,那直线a和b也互相平行。( )
14.两条直线垂直,交点处一定有90°的角。( )
15.只要不相交的两条直线就一定是平行线。( )
四、解答题
16.把下面的图补成一个长方形,量出必须的数据(精确到整厘米数),并计算出这个长方形的面积。
17.要从幸福小区向小河挖一条通水管道,要使管道最短,应该怎样挖?请你在图上画出来。
18.如下图,小熊在A点,小羚羊在B点,它们渴极了,都要到河边喝水,为了让它们尽快喝到水,请你为它们设计出到河边的最短路线,在图上画出来,并说明理由。
19.在正方形ABCD中,哪些线段互相垂直?
20.
(1)量一量,图中∠1是( )度,这是一个( )角。
(2)如果上面方格图中给定的线段AC是等腰梯形的一条腰,AB为这个等腰梯形的上底,请把这个等腰梯形画完整。
(3)画出这个等腰梯形的一条高。
参考答案:
1.A
【分析】根据垂直的性质:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行,也可以根据题目作图帮助解答。
【详解】
图中直线b和直线c都是垂直与直线a的,可以看出直线b和直线c互相平行。
故答案为:A
【点睛】本题考查在同一平面内两条直线的位置判定,应熟练掌握平行和垂直的概念及性质并灵活运用。
2.A
【分析】四边形就是四条线段围成的图形,有四条边,四个角,据此解答。
【详解】正方形、长方形、平行四边形和梯形都具有四边形的特征,属于四边形。
故答案为:A
【点睛】本题主要考查了四边形的特征。
3.A
【分析】钟面上一大格是90°。9点钟时,钟表的时针指向数字9,分针指向12,时针和分针之间有3个大格,是90度,即时针和分针互相垂直,据此解答即可。
【详解】上午9时,钟面上的时针和分针互相垂直;
故选:A。
【点睛】本题考查了角的度量,以及钟面上的角,关键要知道钟面一周平均分60格,钟面上每一大格的度数为360°÷12=30°。
4.C
【分析】先判断哪个是垂线段,再根据点到直线的距离,垂线段最短,即可解答。
【详解】由图可知AD是点A到BC的垂线段,根据点到直线的距离,垂线段最短可知AD最短。
所以答案为:C
【点睛】点到直线的距离垂线段最短。
5.C
【分析】根据度量角的定义和长方形以及平行四边形的特征判断分析即可。
【详解】A.将圆平均分成360份,其中一份所对的角作为度量角的单位,是正确的;
B.把一个长方形框架拉成一个平行四边形,四条边的长度都没变,所以周长不变,是正确的;
C.从平行四边形的一个顶点出发可以画出两条高;故此选项错误;
D.两组对边平行且相等的四边形一定是平行四边形,是正确的。
所以答案为:C
【点睛】本题为综合题 ,掌握度量角的知识和长方形和平行四边形的特征是解题的关键。
6. ①③④ ② d∥c ③ m⊥n
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足,垂直用“⊥”表示。同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线,平行用“//”表示。在同一平面内的两条直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
【详解】图中各组直线中两条直线的位置关系,是相交关系的有①③④ (填序号),互相平行的有②(填序号),可表示为d∥c,互相垂直的有③(填序号),可表示为m⊥n。
【点睛】本题主要考查学生对相交、垂直和平行概念的掌握和灵活运用。
7.平行
【分析】
根据垂直和平行的性质可知,同一平面内,a⊥b,b⊥c,则a∥c。即同一平面内,垂直于同一条直线的两条直线互相平行。
【详解】在同一平面内,直线a垂直于直线b,直线b垂直于直线c(三条直线均不重合),那么直线a与直线c的位置关系是互相平行。
【点睛】熟练掌握平行和垂直的定义是解决本题的关键,画图能帮助学生更好的理解。
8. 无数 两 一
【分析】
从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。则平行四边形和梯形均有无数条高。平行四边形有两组对边平行,而梯形只有一组对边平行。据此解答。
【详解】平行四边形和梯形都有无数 条高,平行四边形有两组对边分别平行,梯形有一组对边平行。
【点睛】本题考查平行四边形和梯形的性质,平行四边形有两组高,无数条高。梯形有一组高,无数条高。
9. 3 3
【分析】两组对边分别平行的四边形,叫做平行四边形;只有一组对边平行的四边形叫做梯形;依此计算出它们的个数即可。
【详解】1+1+1=3(个),即图中有3个平行四边形;
1+1+1=3(个),即图中有3个梯形。
【点睛】熟练掌握梯形和平行四边形的特点是解答此题的关键。
10. 梯形 三角形
【分析】在一张平行四边形纸片上剪一刀可能变成:①一个三角形和一个梯形;②两个三角形;③两个平行四边形;④两个梯形,由此求解。
【详解】如果在一张平行四边形纸上剪一刀,使剪下的两个图形中有一个是梯形,则另一个图形可能是梯形或三角形。
【点睛】本题考查学生的动手操作能力,可以在练习本上画一画可能的情况。
11.×
【分析】两个完全一样的梯形能拼成一个平行四边形,等底等高的梯形并不一定会是完全一样的,据此分析。
【详解】如图,两个梯形等底等高,不一定能拼成一个平行四边形。
故答案为:×
【点睛】关键是熟悉平行四边形特征,注意“完全一样”的梯形才可以拼成平行四边形,不是等底等高。
12.√
【分析】连接直线外一点与直线各点的所有线段中,垂线段最短,据此解答。
【详解】过直线外一点向已知直线画垂线,只能画一条。
故答案为:√
【点睛】熟练掌握垂线段的定义并灵活应用是解答此题的关键。
13.√
【分析】利用平行公理的推论直接作答。
【详解】平行的推论:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也平行。
故答案为:√
【点睛】理解和掌握平行的推论,是解答此题的关键所在。
14.√
【分析】根据垂直的定义:同一平面内,两条直线相交,组成的四个角中,有一个角是直角,这两条直线就互相垂直。
【详解】两条直线垂直,交点处一定有90°的角。
故答案为:√
【点睛】熟练掌握垂直的定义是解答此题的关键。
15.×
【详解】在同一平面内,永不相交的两条直线叫做平行线。如下图所示:
故答案为:×
16.见详解
【分析】长方形的两组对边分别互相平行,两组对边分别相等,四个角都是直角;
根据测量长度的方法量出长方形的长和宽,并根据长方形的特点把此图补成一个长方形,长方形的面积=长×宽,依此计算出长方形的面积即可。
【详解】
面积为:3×5=15(平方厘米)
答:这个长方形的面积是15平方厘米。
【点睛】此题考查的是长方形的特点,以及长方形的面积的计算,应熟练掌握。
17.从幸福小区到小河作垂线段;画图见详解
【分析】根据从直线外一点到这条直线所画的垂直线段最短,要从幸福小区向小河挖一条通水管道,要使管道最短,就要从幸福小区到小河作垂线段。
【详解】要使管道最短,就要从幸福小区到小河作垂线段;画图如下:
【点睛】本题考查了学生对垂线段最短的掌握情况,同时检查了学生的作图能力,及利用数学知识解决实际问题的能力。注意垂线段最短。
18.图见详解;从直线外一点到这条直线的线段中,垂直线段最短
【分析】过直线上或直线外一点作垂线的步骤:
1、把三角尺的一条直角边与已知直线重合。
2、沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。
3、沿三角尺的另一条直角边画一条直线,并画上垂直符号。
这条直线就是已知直线的垂线。
过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
【详解】作图如下:
理由:从直线外一点到这条直线的线段中,垂直线段最短
【点睛】过直线外一点,画已知直线的平行线可以借助直尺和三角尺来完成。
19.见详解
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。据此解答即可。
【详解】AB⊥BC;AB⊥AD;CD⊥AD;CD⊥BC;AC⊥BD
【点睛】本题考查垂直的性质,要判断哪两条线段互相垂直,就看哪两条线段的夹角是直角。
20.(1)130;钝;
(2)(3)见详解
【分析】(1)用量角器测量出∠1的度数,并根据度数判断这是一个什么角。
(2)过点C向右画10个格长的线段,并且平行于线段AB,连接B点与刚画线段的另一个端点所成的图形就是等腰梯形。
(3)梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线,用三角板的直角可以画出梯形的一条高。
【详解】(1)量一量,图中∠1是(130)度,这是一个(钝)角。
(2)(3)
【点睛】熟悉等腰梯形的特征是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
