人教版七年级下册6.1 平方根(第1课时)课件(共19张PPT)
文档属性
| 名称 | 人教版七年级下册6.1 平方根(第1课时)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 22:42:56 | ||
图片预览






文档简介
(共19张PPT)
6.1平方根第一课时
第六章 实数
人教版
七年级下册
学
习
目
标
1.了解算术平方根的概念,会用根号表示一个非负数的算术平方根。
2.会求一些数的算术平方根。
情境
导
入
问题1.学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
边长为5dm。
你是怎样算出来的?
因为5 =25,所以这个正方形画布的边长应取5dm。
情境
导
入
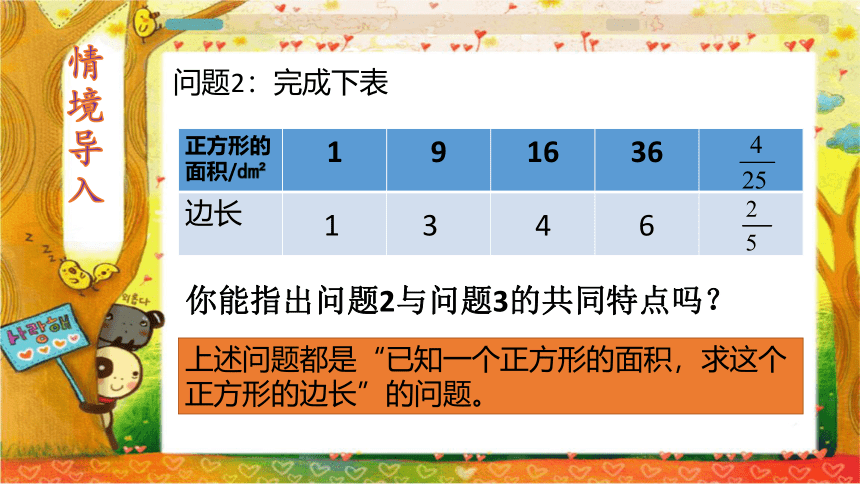
问题2:完成下表
正方形的面积/dm 1 9 16 36
边长
1
6
4
3
你能指出问题2与问题3的共同特点吗?
上述问题都是“已知一个正方形的面积,求这个正方形的边长”的问题。
情境
导
入
上述问题都是“已知一个正方形的面积,求这个正方形的边长”的问题。
“已知一个正数的平方,求这个正数的”的问题。
教学新知
一 算术平方根的概念和表示方法
正数3的平方等于9,我们把正数3叫做9的算术平方根;
正数4的平方等于16,我们把正数4叫做16的算术平方根:
你能说说6和36这两个数吗?
正数6的平方等于36,我们把6叫做36的算术平方根.
教
学
新
知
你能再说说1和1这两个数吗?
正数1的平方等于1,我们把1叫做1的算术平方根。
那么5和25呢?
那么什么是算术平方根呢?
一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根。
教
学
新
知
请同学们拿出提前准备好这样的10张卡片,一面写1~10,另一面写1~10的平方.生任意抽一张卡片,让其他学生回答平方或算术平方根.
合作学习
教
学
新
知
为了书写方便,我们把a的算术平方根记作
一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根。
根号
被开方数
教
学
新
知
0的算术平方根是多少?“怎样表示”比较合适呢?
“0的算术平方根是0”,
算术平方根的概念包含“正数算术平方根”的定义和“0的算术平方根”的规定两部分。
规定,0的算术平方根是0.
教
学
新
知
对于算术平方根中被开方数可以是哪些数?
算术平方根中被开方数可以是正数或0,
即非负数,
为什么负数没有算术平方根呢?
因为任何一个数的平方都不可能是负数。
教
学
新
知
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.0001;
(1)因为10 =100,
二 算术平方根的求法
所以100的算术平方根是10,
即
教
学
新
知
例1:求下列各数的算术平方根:
(2) ;
(2)因为
二 算术平方根的求法
所以 的算术平方根是
即
教
学
新
知
例1:求下列各数的算术平方根:
(3)0.0001;
(3)因为(0.01) =0.0001,
二 算术平方根的求法
所以 0.0001 的算术平方根是 0.01,
即
教
学
新
知
从上述例题中,你能发现被开方数的大小与对应的算术平方根的大小之间有什么关系吗?
被开方数越大,对应的算术平方根也越大.
巩
固
练
习
1.下列说法正确的个数是( ).
①-5是一25的算术平方根;
②6是6 的算术平方根;
③0的算术平方根是0;
④0.01 是 0.1 的算术平方根;
⑤一个正方形的边长就是这个正方形的面积的算术平方根。
D
A.0个 B.1个 C.2个 D.3个
巩
固
练
习
2. 下列各数的算术平方根:
(1)49; (2)0.25; (3) ; (4) ;
总
结
提
升
通过本节课的学习,你有哪些收获
1.什么是算术平方根
2.如何求一个正数的算术平方根
3.什么数才有算术平方根?
谢谢观看!
6.1平方根第一课时
第六章 实数
人教版
七年级下册
学
习
目
标
1.了解算术平方根的概念,会用根号表示一个非负数的算术平方根。
2.会求一些数的算术平方根。
情境
导
入
问题1.学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
边长为5dm。
你是怎样算出来的?
因为5 =25,所以这个正方形画布的边长应取5dm。
情境
导
入
问题2:完成下表
正方形的面积/dm 1 9 16 36
边长
1
6
4
3
你能指出问题2与问题3的共同特点吗?
上述问题都是“已知一个正方形的面积,求这个正方形的边长”的问题。
情境
导
入
上述问题都是“已知一个正方形的面积,求这个正方形的边长”的问题。
“已知一个正数的平方,求这个正数的”的问题。
教学新知
一 算术平方根的概念和表示方法
正数3的平方等于9,我们把正数3叫做9的算术平方根;
正数4的平方等于16,我们把正数4叫做16的算术平方根:
你能说说6和36这两个数吗?
正数6的平方等于36,我们把6叫做36的算术平方根.
教
学
新
知
你能再说说1和1这两个数吗?
正数1的平方等于1,我们把1叫做1的算术平方根。
那么5和25呢?
那么什么是算术平方根呢?
一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根。
教
学
新
知
请同学们拿出提前准备好这样的10张卡片,一面写1~10,另一面写1~10的平方.生任意抽一张卡片,让其他学生回答平方或算术平方根.
合作学习
教
学
新
知
为了书写方便,我们把a的算术平方根记作
一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根。
根号
被开方数
教
学
新
知
0的算术平方根是多少?“怎样表示”比较合适呢?
“0的算术平方根是0”,
算术平方根的概念包含“正数算术平方根”的定义和“0的算术平方根”的规定两部分。
规定,0的算术平方根是0.
教
学
新
知
对于算术平方根中被开方数可以是哪些数?
算术平方根中被开方数可以是正数或0,
即非负数,
为什么负数没有算术平方根呢?
因为任何一个数的平方都不可能是负数。
教
学
新
知
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.0001;
(1)因为10 =100,
二 算术平方根的求法
所以100的算术平方根是10,
即
教
学
新
知
例1:求下列各数的算术平方根:
(2) ;
(2)因为
二 算术平方根的求法
所以 的算术平方根是
即
教
学
新
知
例1:求下列各数的算术平方根:
(3)0.0001;
(3)因为(0.01) =0.0001,
二 算术平方根的求法
所以 0.0001 的算术平方根是 0.01,
即
教
学
新
知
从上述例题中,你能发现被开方数的大小与对应的算术平方根的大小之间有什么关系吗?
被开方数越大,对应的算术平方根也越大.
巩
固
练
习
1.下列说法正确的个数是( ).
①-5是一25的算术平方根;
②6是6 的算术平方根;
③0的算术平方根是0;
④0.01 是 0.1 的算术平方根;
⑤一个正方形的边长就是这个正方形的面积的算术平方根。
D
A.0个 B.1个 C.2个 D.3个
巩
固
练
习
2. 下列各数的算术平方根:
(1)49; (2)0.25; (3) ; (4) ;
总
结
提
升
通过本节课的学习,你有哪些收获
1.什么是算术平方根
2.如何求一个正数的算术平方根
3.什么数才有算术平方根?
谢谢观看!
