3.1.2 函数的表示法(第2课时) 课件(共39张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法(第2课时) 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 972.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 16:00:26 | ||
图片预览









文档简介
(共39张PPT)
3.1.2函数的表示法(第2课时)
第 3章 函数的概念与性质
01分段函数求值
02分段函数的应用
目录
03求函数解析式
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.(重点,难点)
2.能在实际问题中列出分段函数,并能解决有关问题.(重点、难点)
学习目标
1.如何理解分段函数,处理分段函数问题的一般思路是怎样的?
注:分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同.
分段函数:对于函数y= (x),若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数y= (x)叫分段函数.
2.函数常见的表示方法有哪几种?各有什么特点各是什么?
(1)解析法;(2)图象法;(3)列表法.
复习引入
1.分段函数求值
总结
练一练
2.分段函数的应用
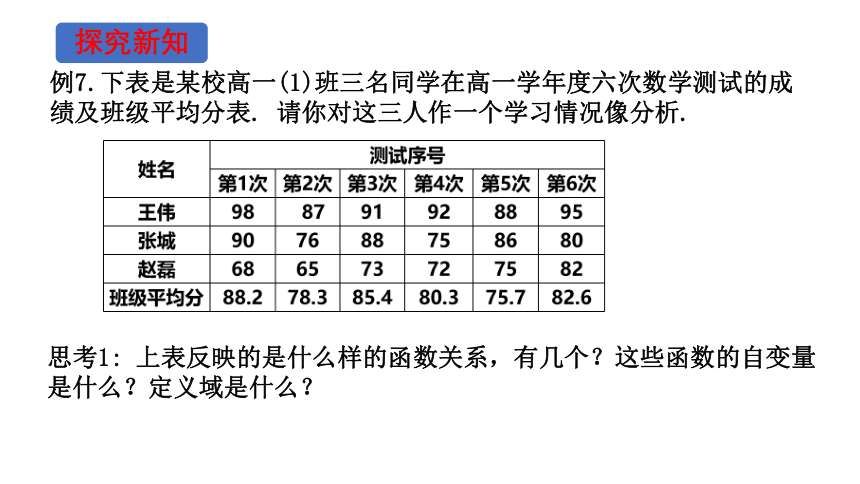
例7.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表. 请你对这三人作一个学习情况像分析.
思考1: 上表反映的是什么样的函数关系,有几个?这些函数的自变量是什么?定义域是什么?
探究新知
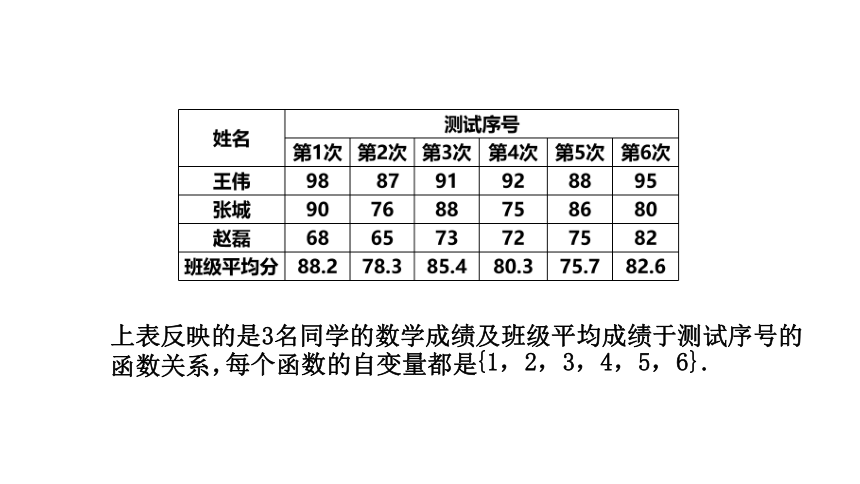
上表反映的是3名同学的数学成绩及班级平均成绩于测试序号的函数关系,
每个函数的自变量都是
{1,2,3,4,5,6}.
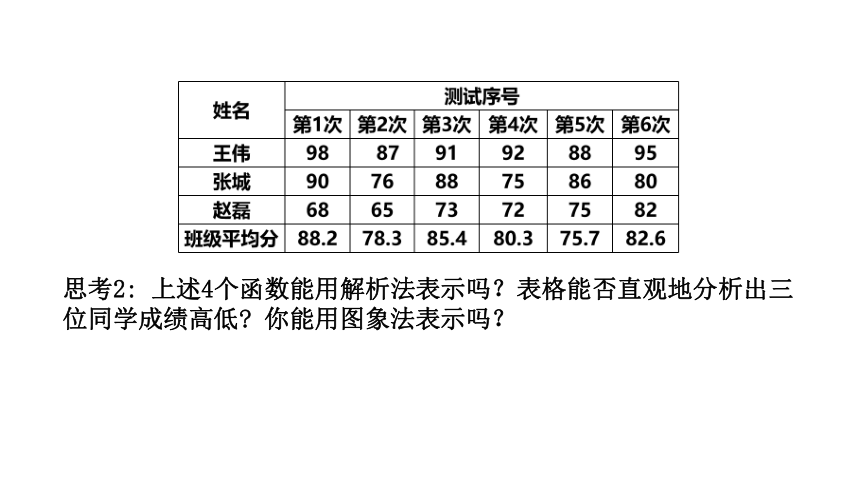
思考2: 上述4个函数能用解析法表示吗?表格能否直观地分析出三位同学成绩高低 你能用图象法表示吗?
解:为了直观地反映每位同学和班级平均成绩的变化情况,我们用图象法将表格中的4个函数表示出来,如图:
可以看出:
王伟同学的数学成绩始终高于平均水平,学习情况稳定且成绩优秀。
张城同学的数学成绩不大稳定,总在班级平均水平上下波动,且波动幅度较大。
赵磊同学的数学成绩低于班级平均水平,但他成绩在稳步提高。
例8 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税). 2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为
个税税额=应纳税所得额×税率 - 速算扣除数.
应纳税所得额的计算公式为
应纳税所得额=综合所得收入额 - 基本减除费用 - 专项扣除 - 专项附加扣除 - 依法确定的其他扣除
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见表3.1-5.
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图像;
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险,基本医疗保险,失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
分析:根据个税产生办法,可按下列步骤计算应缴纳个税税额:
第一步,根据②计算出应纳税所得额t;
第二步,由t的值并根据表 3.1-5 得出相应的税率与速算扣除数;
第三步,根据①计算出个税税额y的值.
由于不同应纳税所得额t对应不同的税率与速算扣除数,所以 y 是 t 的分段函数.
解:(1)根据表3.1-5可得函数 y=f(t)的解析式为:
函数图像如图3.1-7所示:
注意:作分段函数的图像时,定义域分界点处的函数取值情况,决定着图象在分界点处的断开或连接作图时要特别注意标明分界点处的情况.
(2)根据②,小王全年应纳税所得额为
将t代入③得
所以,小王应缴纳的综合所得个税税额为1029.6元.
解应用题的基本步骤:
(1)审题:读懂题意,分清条件与结论,理顺数量关系;
(2)建模:将已知条件转化为数学语言,应用数学知识建立相应的函数模型;
(3)解模:求解函数模型,得到数学结论;
(4)还原:将数学方面的结论还原到实际问题中去,解释实际意义.
问题1:解析法是中学阶段函数的主要表达方法,它是用数学表达式即解析式来表示两个变量之间的对应关系,在这以前我们已学过求解析式的一些方法,你还能记起这些方法吗?
(1)直接法(适用于实际问题):根据函数问题的实际背景直接列出函数的解析式。
(2)待定系数法(含图象法)(适用于已知函数模型的情况):其一般步骤为:设出函数的解析式→列方程(组)→解出参数→代回解析式。
3.求函数解析式
例1.已知函数f(x)是一次函数,且其图象经过点(1,2)和(2,5).
求f(4)的值.(待定系数法)
题型:求函数解析式
解:
由题意得
例2.已知函数f(x)=-2x2-x+1.求函数下列函数的解析式:
(1)f(-x+1); (2)f(x2-1).
解:
∵ f(x)=-2x2-x+1
∴ f(-x+1)=
-2(-x+1)2-(-x+1)+1
=-2x2+5x-2
∴f(x2-1)=
-2(x2-1)2+5(x2-1)-2
=-2x4+3x2
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(1):对应关系f是如何把”x+1”对应到“x2+2x+2”的
∵x2+2x+2=
(x+1)2+1
∴f(x+1)=(x+1)2+1
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(2):由此你能写出f(x)吗 并能标出x的范围吗?
∵在f(x+1)=(x+1)2+1中,x+1<1
∴ 在f(x)=x2+1中,x<1
∴f(x)=x2+1(x<1)
思考(3):这种方法叫“配凑法”,请说说用“配凑法”由f(g(x))求f(x)的一般步骤?
(配凑法)
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(4):如果把x+1换成变量t,如何将“x2+2x+2”用t表示出来
解:设t=x+1,则
t<1,x=t-1
∴x2+2x+2=
(t-1)2+2(t-1)+2
=t2+1
思考(5):你说说对应关系f是怎样的吗?并能由此写出函数f(x)吗?
f(x+1)=f(t)=x2+2x+2=t2+1
∴f(t)=t2+1(t<1)
∴f(x)=x2+1(x<1)
思考(6):这种方法叫“换元法”,请说说用“换元法”由f(g(x))求f(x)的一般步骤?
(换元法)
解:
(方程组法)
课本练习
练习
下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图像写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后,一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
解:
(1)对应(D),(2)对应(A),(3)对应(B);
剩下的图象(C)可以为:我出发后越走越累,所以速度越来越慢.
2:某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价y与里程x之
间的函数解析式,并画出函数的图象.
解:设票价为y元,里程为x公里.
由题意可知,自变量的取值范围是(0,20],由票价制定规则,可得到函数解析式:
练习
某种新产品投放市场的100天中,前40天其价格呈直线上升趋势,而后60天其价格呈
直线下降趋势,现统计出其中4天的价格如下表:
(2)销售量g(x)与时间 x 的函数解析式为 则该产品投放市场第多少天销售额最高?最高为多少元?
(1)写出价格 f(x)关于时间 x 的函数解析式( x 表示投放市场的第 x ( ) 天).
解:(1)由题意,设
时间 第4天 第32天 第60天 第90天
价格/元 23 30 22 7
练习
3. 某种新产品投放市场的100天中,前40天其价格呈直线上升趋势,而后60天其价格呈直线下降趋势,现统计出其中4天的价格如下表:
(2)销售量g(x)与时间 x 的函数解析式为 则该产品投放市场第多少天销售额最高?最高为多少元?
(1)写出价格 f(x)关于时间 x 的函数解析式( x 表示投放市场的第 x ( ) 天).
解:(2)设该产品的日销售额为 h(x),则
时间 第4天 第32天 第60天 第90天
价格/元 23 30 22 7
综上可得,该产品投放市场第10天和第11天销售额最高,最高销售额为808.5元.
随堂检测
课堂小结
1.
2.求函数解析式的方法
课堂小结
3.1.2函数的表示法(第2课时)
第 3章 函数的概念与性质
01分段函数求值
02分段函数的应用
目录
03求函数解析式
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.(重点,难点)
2.能在实际问题中列出分段函数,并能解决有关问题.(重点、难点)
学习目标
1.如何理解分段函数,处理分段函数问题的一般思路是怎样的?
注:分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同.
分段函数:对于函数y= (x),若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数y= (x)叫分段函数.
2.函数常见的表示方法有哪几种?各有什么特点各是什么?
(1)解析法;(2)图象法;(3)列表法.
复习引入
1.分段函数求值
总结
练一练
2.分段函数的应用
例7.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表. 请你对这三人作一个学习情况像分析.
思考1: 上表反映的是什么样的函数关系,有几个?这些函数的自变量是什么?定义域是什么?
探究新知
上表反映的是3名同学的数学成绩及班级平均成绩于测试序号的函数关系,
每个函数的自变量都是
{1,2,3,4,5,6}.
思考2: 上述4个函数能用解析法表示吗?表格能否直观地分析出三位同学成绩高低 你能用图象法表示吗?
解:为了直观地反映每位同学和班级平均成绩的变化情况,我们用图象法将表格中的4个函数表示出来,如图:
可以看出:
王伟同学的数学成绩始终高于平均水平,学习情况稳定且成绩优秀。
张城同学的数学成绩不大稳定,总在班级平均水平上下波动,且波动幅度较大。
赵磊同学的数学成绩低于班级平均水平,但他成绩在稳步提高。
例8 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税). 2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为
个税税额=应纳税所得额×税率 - 速算扣除数.
应纳税所得额的计算公式为
应纳税所得额=综合所得收入额 - 基本减除费用 - 专项扣除 - 专项附加扣除 - 依法确定的其他扣除
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见表3.1-5.
级数 全年应纳税所得额所在区间 税率 (0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图像;
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险,基本医疗保险,失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
分析:根据个税产生办法,可按下列步骤计算应缴纳个税税额:
第一步,根据②计算出应纳税所得额t;
第二步,由t的值并根据表 3.1-5 得出相应的税率与速算扣除数;
第三步,根据①计算出个税税额y的值.
由于不同应纳税所得额t对应不同的税率与速算扣除数,所以 y 是 t 的分段函数.
解:(1)根据表3.1-5可得函数 y=f(t)的解析式为:
函数图像如图3.1-7所示:
注意:作分段函数的图像时,定义域分界点处的函数取值情况,决定着图象在分界点处的断开或连接作图时要特别注意标明分界点处的情况.
(2)根据②,小王全年应纳税所得额为
将t代入③得
所以,小王应缴纳的综合所得个税税额为1029.6元.
解应用题的基本步骤:
(1)审题:读懂题意,分清条件与结论,理顺数量关系;
(2)建模:将已知条件转化为数学语言,应用数学知识建立相应的函数模型;
(3)解模:求解函数模型,得到数学结论;
(4)还原:将数学方面的结论还原到实际问题中去,解释实际意义.
问题1:解析法是中学阶段函数的主要表达方法,它是用数学表达式即解析式来表示两个变量之间的对应关系,在这以前我们已学过求解析式的一些方法,你还能记起这些方法吗?
(1)直接法(适用于实际问题):根据函数问题的实际背景直接列出函数的解析式。
(2)待定系数法(含图象法)(适用于已知函数模型的情况):其一般步骤为:设出函数的解析式→列方程(组)→解出参数→代回解析式。
3.求函数解析式
例1.已知函数f(x)是一次函数,且其图象经过点(1,2)和(2,5).
求f(4)的值.(待定系数法)
题型:求函数解析式
解:
由题意得
例2.已知函数f(x)=-2x2-x+1.求函数下列函数的解析式:
(1)f(-x+1); (2)f(x2-1).
解:
∵ f(x)=-2x2-x+1
∴ f(-x+1)=
-2(-x+1)2-(-x+1)+1
=-2x2+5x-2
∴f(x2-1)=
-2(x2-1)2+5(x2-1)-2
=-2x4+3x2
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(1):对应关系f是如何把”x+1”对应到“x2+2x+2”的
∵x2+2x+2=
(x+1)2+1
∴f(x+1)=(x+1)2+1
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(2):由此你能写出f(x)吗 并能标出x的范围吗?
∵在f(x+1)=(x+1)2+1中,x+1<1
∴ 在f(x)=x2+1中,x<1
∴f(x)=x2+1(x<1)
思考(3):这种方法叫“配凑法”,请说说用“配凑法”由f(g(x))求f(x)的一般步骤?
(配凑法)
例3:若函数f(x+1)=x2+2x+2(x<0), 求函数f(x)?
思考(4):如果把x+1换成变量t,如何将“x2+2x+2”用t表示出来
解:设t=x+1,则
t<1,x=t-1
∴x2+2x+2=
(t-1)2+2(t-1)+2
=t2+1
思考(5):你说说对应关系f是怎样的吗?并能由此写出函数f(x)吗?
f(x+1)=f(t)=x2+2x+2=t2+1
∴f(t)=t2+1(t<1)
∴f(x)=x2+1(x<1)
思考(6):这种方法叫“换元法”,请说说用“换元法”由f(g(x))求f(x)的一般步骤?
(换元法)
解:
(方程组法)
课本练习
练习
下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图像写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后,一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
解:
(1)对应(D),(2)对应(A),(3)对应(B);
剩下的图象(C)可以为:我出发后越走越累,所以速度越来越慢.
2:某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价y与里程x之
间的函数解析式,并画出函数的图象.
解:设票价为y元,里程为x公里.
由题意可知,自变量的取值范围是(0,20],由票价制定规则,可得到函数解析式:
练习
某种新产品投放市场的100天中,前40天其价格呈直线上升趋势,而后60天其价格呈
直线下降趋势,现统计出其中4天的价格如下表:
(2)销售量g(x)与时间 x 的函数解析式为 则该产品投放市场第多少天销售额最高?最高为多少元?
(1)写出价格 f(x)关于时间 x 的函数解析式( x 表示投放市场的第 x ( ) 天).
解:(1)由题意,设
时间 第4天 第32天 第60天 第90天
价格/元 23 30 22 7
练习
3. 某种新产品投放市场的100天中,前40天其价格呈直线上升趋势,而后60天其价格呈直线下降趋势,现统计出其中4天的价格如下表:
(2)销售量g(x)与时间 x 的函数解析式为 则该产品投放市场第多少天销售额最高?最高为多少元?
(1)写出价格 f(x)关于时间 x 的函数解析式( x 表示投放市场的第 x ( ) 天).
解:(2)设该产品的日销售额为 h(x),则
时间 第4天 第32天 第60天 第90天
价格/元 23 30 22 7
综上可得,该产品投放市场第10天和第11天销售额最高,最高销售额为808.5元.
随堂检测
课堂小结
1.
2.求函数解析式的方法
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
