2.1.1 倾斜角与斜率(第二课时)课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共19张PPT)
文档属性
| 名称 | 2.1.1 倾斜角与斜率(第二课时)课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 403.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 16:05:44 | ||
图片预览




文档简介
(共19张PPT)
2.1.1 倾斜角与斜率
(第二课时)
一、直线的倾斜角与斜率
1.直线的倾斜角:
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线l 与x轴相交时,我们取x轴作为基准,x轴正方向与直线l 向上方向之间所成的角α叫做直线l 的倾斜角.
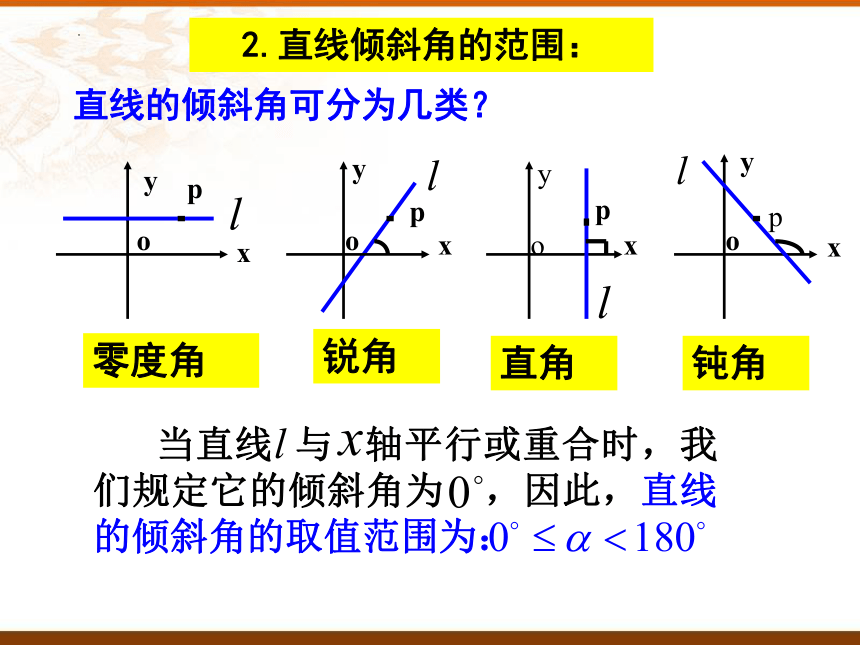
2.直线倾斜角的范围:
零度角
锐角
直角
钝角
直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
二、直线的斜率
1、直线斜率的定义:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。用小写字母 k 表示,即:
例如:
x
.
P
y
O
x
.
P
y
O
x
.
P
y
O
x
.
P
y
O
(1)
(2)
(4)
(3)
o
o
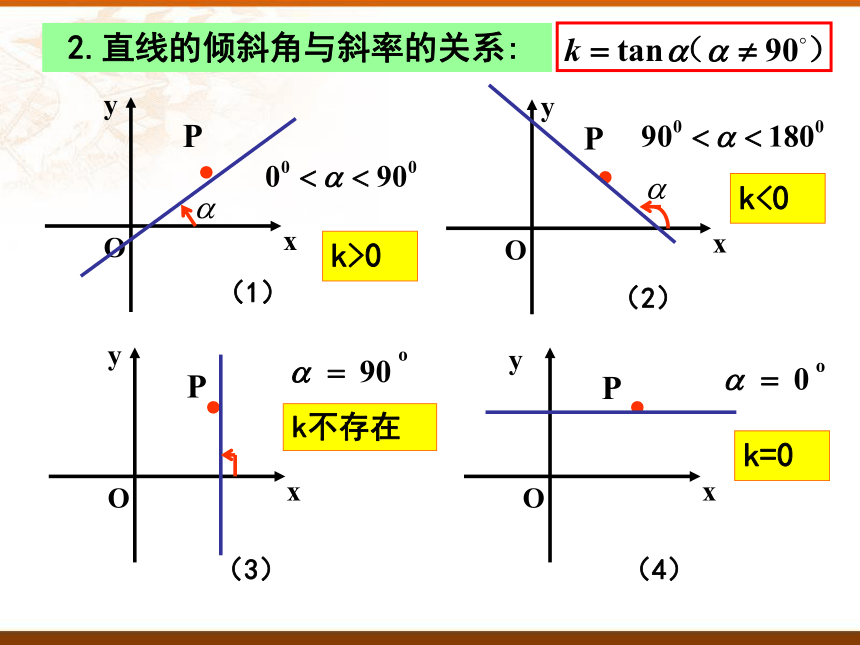
k>0
k<0
k不存在
k=0
2.直线的倾斜角与斜率的关系:
1.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α
B.180°-α
C.180°-α或90°-α
D.90°+α或90°-α
学以致用:
D
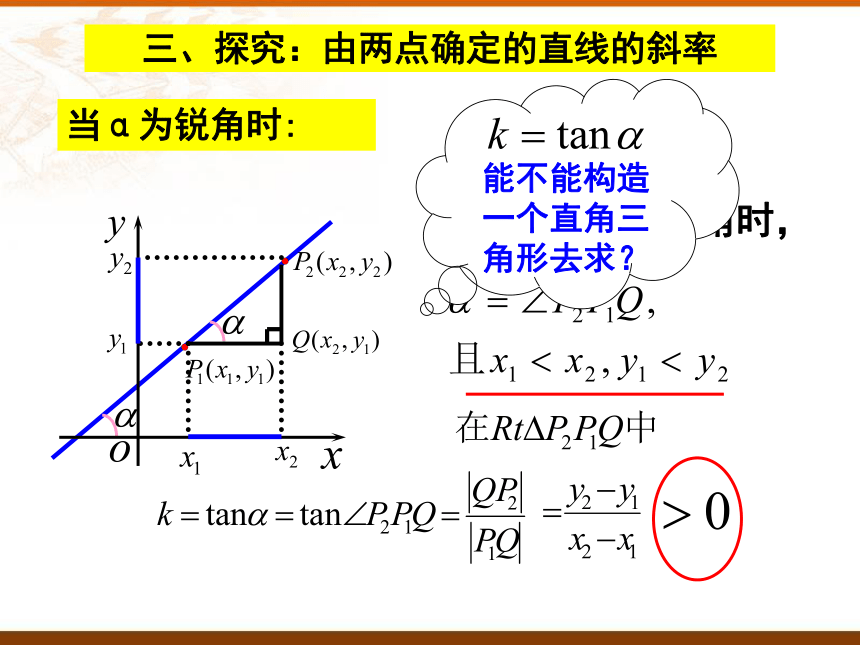
三、探究:由两点确定的直线的斜率
如图,当α为锐角时,
能不能构造一个直角三角形去求?
当α为锐角时:
如图,当α为钝角时,
当α为钝角时:
当直线平行于x轴,或与x轴重合时,上述公式还成立吗?为什么?
答:成立,此时y1=y2 ,因为分子为0,分母不为0,所以此时k=0
思考1:
思考?
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢?
(1)已知直线上两点 、 ,运用上述公式计算直线AB的斜率时,与A、B两点坐标的顺序有关吗?
答:与A、B两点的顺序无关。
思考2:
直线的斜率公式:
综上所述,我们得到经过两点
的直线的斜率公式:
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:不适用,此时x1=x2 ,因为分母为0,所以k不存在。
思考2:
3.直线的斜率公式
如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
例1:
在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
O
x
y
A3
A1
A2
A4
例2:
四、练习:
1、解:
(1) ;(2)
(3)
(4)
请看课本P55页第1题
3、解:(1)因为
所以 ,因此,直线AB的倾斜角是 ;
(2)因为过C,D两点的直线垂直x轴,所以
直线CD的倾斜角是 ;
(3)因为 ,所以 ,因此,
直线PQ的倾斜角是 。
四、练习:
请看课本P55页第3题
学以致用:
2.1.1 倾斜角与斜率
(第二课时)
一、直线的倾斜角与斜率
1.直线的倾斜角:
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线l 与x轴相交时,我们取x轴作为基准,x轴正方向与直线l 向上方向之间所成的角α叫做直线l 的倾斜角.
2.直线倾斜角的范围:
零度角
锐角
直角
钝角
直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
二、直线的斜率
1、直线斜率的定义:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。用小写字母 k 表示,即:
例如:
x
.
P
y
O
x
.
P
y
O
x
.
P
y
O
x
.
P
y
O
(1)
(2)
(4)
(3)
o
o
k>0
k<0
k不存在
k=0
2.直线的倾斜角与斜率的关系:
1.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α
B.180°-α
C.180°-α或90°-α
D.90°+α或90°-α
学以致用:
D
三、探究:由两点确定的直线的斜率
如图,当α为锐角时,
能不能构造一个直角三角形去求?
当α为锐角时:
如图,当α为钝角时,
当α为钝角时:
当直线平行于x轴,或与x轴重合时,上述公式还成立吗?为什么?
答:成立,此时y1=y2 ,因为分子为0,分母不为0,所以此时k=0
思考1:
思考?
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢?
(1)已知直线上两点 、 ,运用上述公式计算直线AB的斜率时,与A、B两点坐标的顺序有关吗?
答:与A、B两点的顺序无关。
思考2:
直线的斜率公式:
综上所述,我们得到经过两点
的直线的斜率公式:
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:不适用,此时x1=x2 ,因为分母为0,所以k不存在。
思考2:
3.直线的斜率公式
如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
例1:
在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
O
x
y
A3
A1
A2
A4
例2:
四、练习:
1、解:
(1) ;(2)
(3)
(4)
请看课本P55页第1题
3、解:(1)因为
所以 ,因此,直线AB的倾斜角是 ;
(2)因为过C,D两点的直线垂直x轴,所以
直线CD的倾斜角是 ;
(3)因为 ,所以 ,因此,
直线PQ的倾斜角是 。
四、练习:
请看课本P55页第3题
学以致用:
