3.1.2 函数的表示法 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共22张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 16:39:20 | ||
图片预览



文档简介
(共22张PPT)
3.1 函数的概念及其表示
3.1.2 函数的表示
人教A版(2019)
一、复习旧知、引入课题
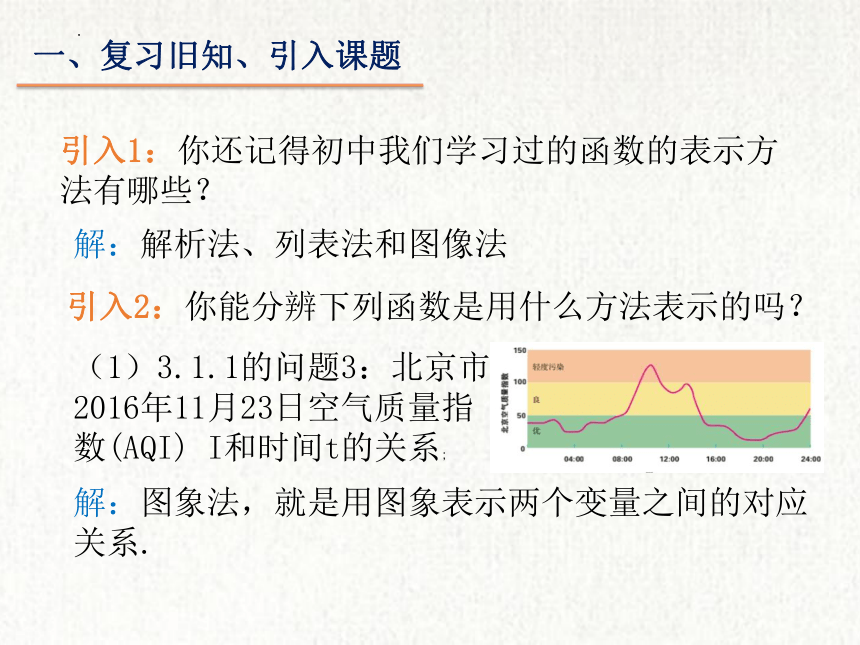
解:图象法,就是用图象表示两个变量之间的对应关系.
引入1:你还记得初中我们学习过的函数的表示方法有哪些?
解:解析法、列表法和图像法
引入2:你能分辨下列函数是用什么方法表示的吗?
(1)3.1.1的问题3:北京市
2016年11月23日空气质量指
数(AQI) I和时间t的关系;
一、复习旧知、引入课题
引入2:你能分辨下列函数是用什么方法表示的吗?
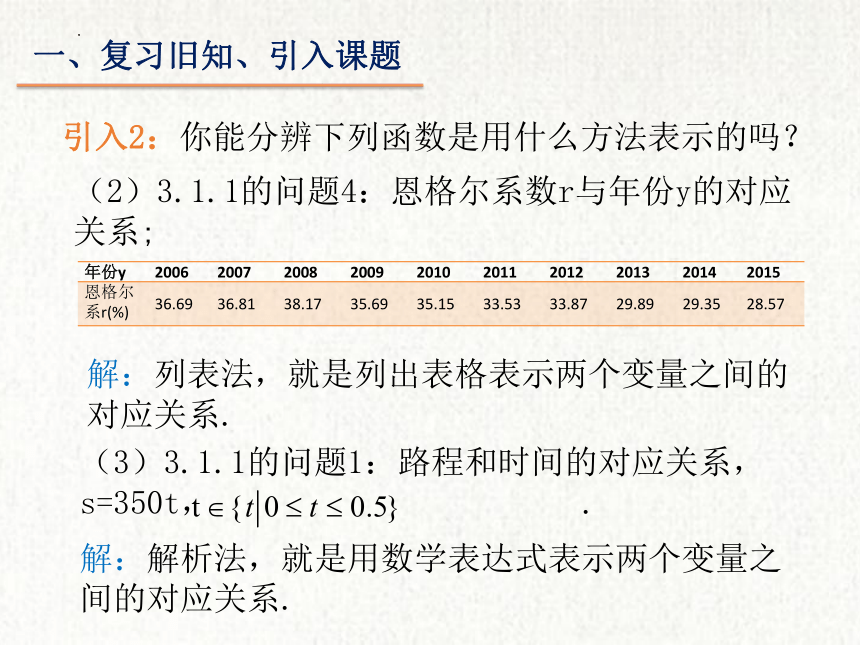
(2)3.1.1的问题4:恩格尔系数r与年份y的对应关系;
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
恩格尔系r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35 28.57
解:列表法,就是列出表格表示两个变量之间的对应关系.
(3)3.1.1的问题1:路程和时间的对应关系,s=350t, .
解:解析法,就是用数学表达式表示两个变量之间的对应关系.
二、制定目标、把握方向
三、创设情境、提出问题
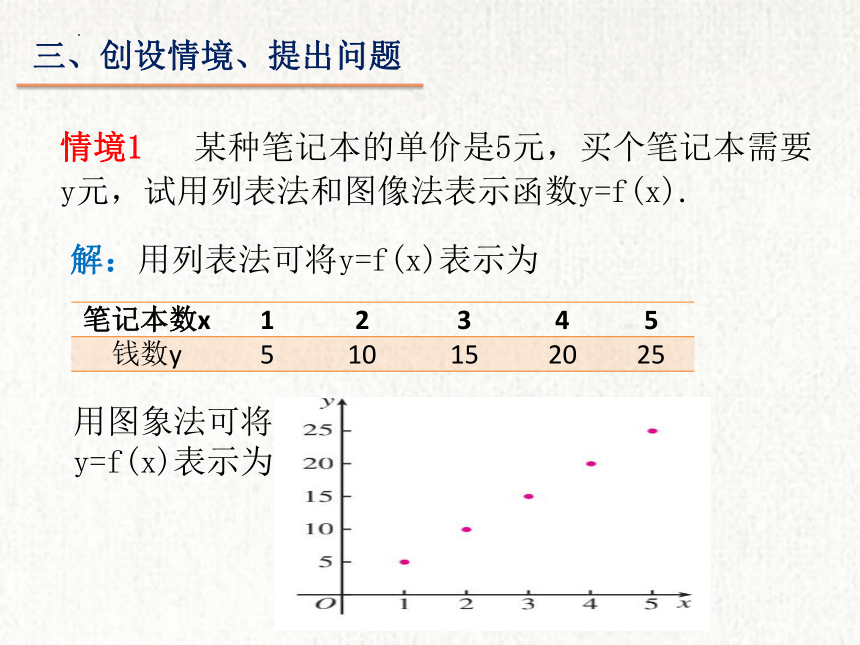
情境1 某种笔记本的单价是5元,买个笔记本需要y元,试用列表法和图像法表示函数y=f(x).
解:用列表法可将y=f(x)表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
用图象法可将
y=f(x)表示为
三、创设情境、提出问题
追问1:你发现图象上这些点有什么特征?
追问2:那你能写出它的解析式吗??
解:这些点好像都经过一条直线。
解:y=f(x)的解析式可写为y=5x, ,
可以看出确实是一次函数上的几个点。
三、创设情境、提出问题
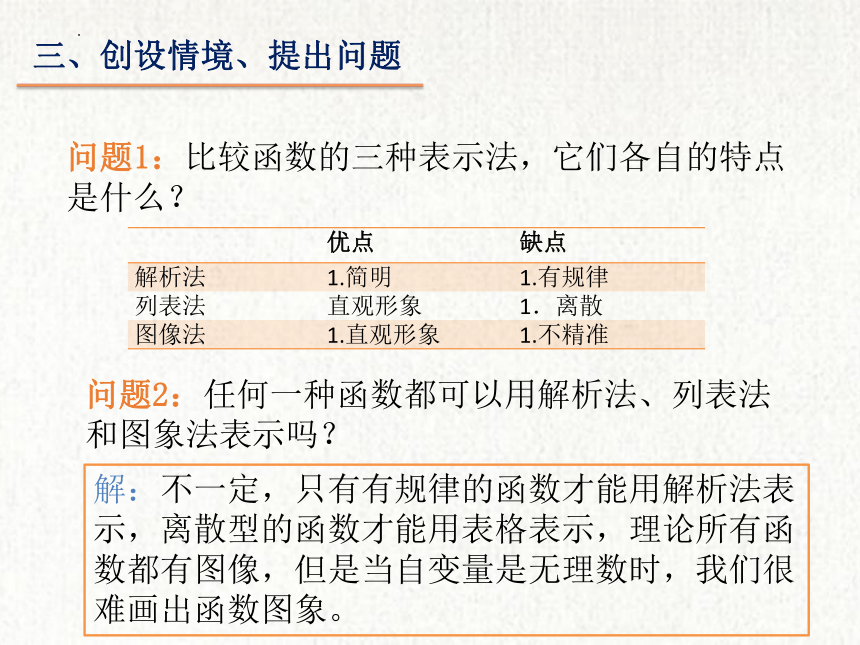
问题1:比较函数的三种表示法,它们各自的特点是什么?
优点 缺点
解析法 1.简明 1.有规律
列表法 直观形象 1.离散
图像法 1.直观形象 1.不精准
问题2:任何一种函数都可以用解析法、列表法和图象法表示吗?
解:不一定,只有有规律的函数才能用解析法表示,离散型的函数才能用表格表示,理论所有函数都有图像,但是当自变量是无理数时,我们很难画出函数图象。
三、例题练习、巩固理解
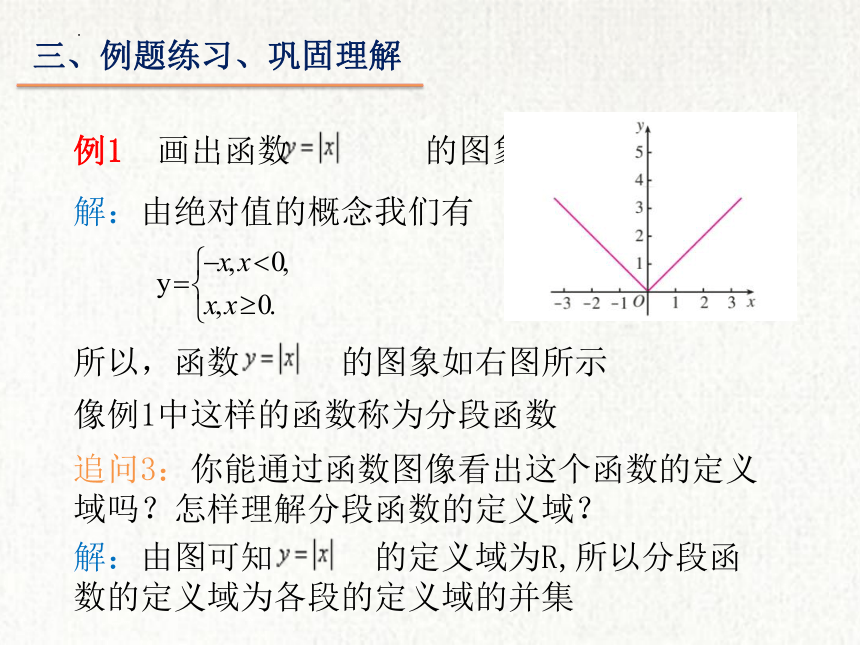
例1 画出函数 的图象
解:由绝对值的概念我们有
所以,函数 的图象如右图所示
像例1中这样的函数称为分段函数
追问3:你能通过函数图像看出这个函数的定义域吗?怎样理解分段函数的定义域?
解:由图可知 的定义域为R,所以分段函数的定义域为各段的定义域的并集
三、例题练习、巩固理解
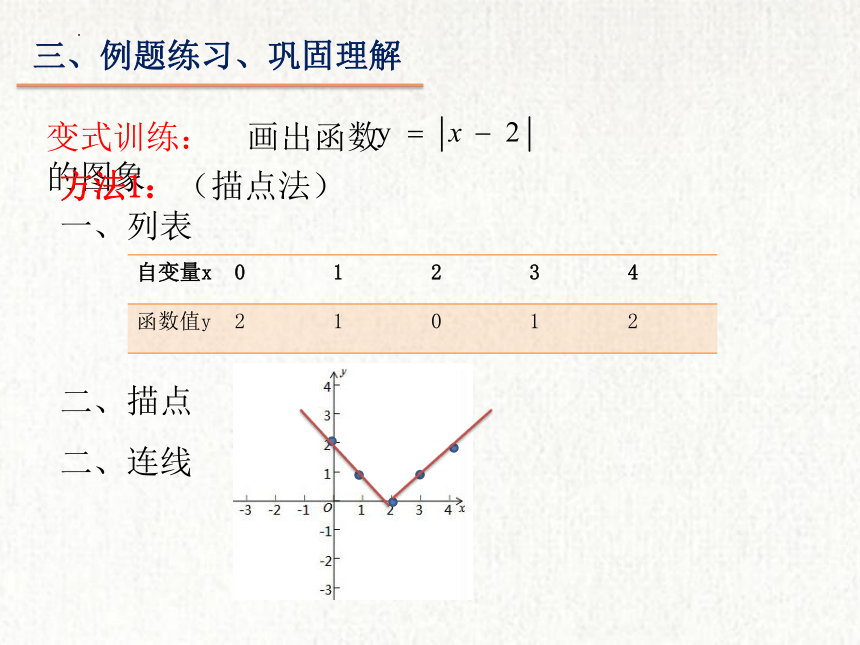
变式训练: 画出函数 的图象
方法1:(描点法)
一、列表
自变量x 0 1 2 3 4
函数值y 2 1 0 1 2
二、描点
二、连线
三、例题练习、巩固理解
变式训练: 画出函数 的图象
方法2:(去绝对值)
解:由绝对值的概念我们有
所以,函数 的图象如右图所示
三、例题练习、巩固理解
变式训练: 画出函数 的图象
方法3:(平移法)
解:由初中所学知识,可知
所以,函数 的图象如右图所示
的图象可由
的图象向右平移两个单位
得到。
例2 给定函数 ,
(1)在同一直角坐标系中画出f(x),g(x)的图像;
(2)用M(x)表示f(x),g(x)中的最大者,记为
M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)} =max{3,9}=9.
请分别用图象法和解析式法表示M(x)
三、例题练习、巩固理解
解:(1)在同一坐标
系中画出f(x),g(x)
的图象如图1所示
(图1)
三、例题练习、巩固理解
解:(2)(方法一)由图1函数取值的情况,结合M(x)的定义,可得M(x)的图象如图2所示,
(图2)
结合图2,
得M(x)的解析式为
例2 给定函数 ,
(2)用M(x)表示f(x),g(x)中的最大者,记为M(x)=
max{f(x),g(x)},请分别用图象法和解析式法表示M(x)
例2 给定函数 ,
(2)用M(x)表示f(x),g(x)中的最大者,记为M(x)=
max{f(x),g(x)}.请分别用图象法和解析式法表示M(x)
三、例题练习、巩固理解
解:(2)(方法二)类比比较数的大小,我们可以用两个函数相减,
得M(x)的解析式为
四、选择方法、情境应用
情境2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
测试成绩 第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请对这三位同学在高一学年度的数学学习情况做分析.
姓名
解析:从表中可以知道每位同学在每次测试中的成绩,但不容易看出每位同学的成绩的变化情况.可将“成绩”与“测试序号”之间的关系用函数图象表示,如图,可以较直观地看到成绩变化情况.
四、选择方法、情境应用
四、选择方法、情境应用
解析:由图可知王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定.张诚同学成绩不稳定,在班级平均水平上下波动,且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
四、选择方法、情境应用
情境3 依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税)。2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数 ①。应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除 ②。其中,“基本减除费用”(免征额)为每年60000元。税率与速算扣除数见下表。
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1 [0,36 000] 3 0
2 (36 000,144 000] 10 2520
3 (144 000,300 000] 20 16920
4 (300 000,420 000] 25 31920
5 (420 000,660 000] 30 52910
6 (660 000,960 000] 35 85920
7 (960 000,) 45 181920
四、选择方法、情境应用
情境3:(1) 设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图象。
解析: 根据上表,可得函数y=f(t)的解析式为
四、选择方法、情境应用
情境3:(1) 设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图象。
解析:根据上表,可得函数y=f(t)的图象为
四、选择方法、情境应用
情境3:(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
解析:根据公式②,小王全年应缴纳所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8×189600-117360=34320
将t的值代入③,得
y=0.03×34320=1029.6
所以,小王应缴纳的综合所得个税税额为1029.6元。
五、小结提升、形成结构
学习了本节课,你有什么收获?
3.1 函数的概念及其表示
3.1.2 函数的表示
人教A版(2019)
一、复习旧知、引入课题
解:图象法,就是用图象表示两个变量之间的对应关系.
引入1:你还记得初中我们学习过的函数的表示方法有哪些?
解:解析法、列表法和图像法
引入2:你能分辨下列函数是用什么方法表示的吗?
(1)3.1.1的问题3:北京市
2016年11月23日空气质量指
数(AQI) I和时间t的关系;
一、复习旧知、引入课题
引入2:你能分辨下列函数是用什么方法表示的吗?
(2)3.1.1的问题4:恩格尔系数r与年份y的对应关系;
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
恩格尔系r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35 28.57
解:列表法,就是列出表格表示两个变量之间的对应关系.
(3)3.1.1的问题1:路程和时间的对应关系,s=350t, .
解:解析法,就是用数学表达式表示两个变量之间的对应关系.
二、制定目标、把握方向
三、创设情境、提出问题
情境1 某种笔记本的单价是5元,买个笔记本需要y元,试用列表法和图像法表示函数y=f(x).
解:用列表法可将y=f(x)表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
用图象法可将
y=f(x)表示为
三、创设情境、提出问题
追问1:你发现图象上这些点有什么特征?
追问2:那你能写出它的解析式吗??
解:这些点好像都经过一条直线。
解:y=f(x)的解析式可写为y=5x, ,
可以看出确实是一次函数上的几个点。
三、创设情境、提出问题
问题1:比较函数的三种表示法,它们各自的特点是什么?
优点 缺点
解析法 1.简明 1.有规律
列表法 直观形象 1.离散
图像法 1.直观形象 1.不精准
问题2:任何一种函数都可以用解析法、列表法和图象法表示吗?
解:不一定,只有有规律的函数才能用解析法表示,离散型的函数才能用表格表示,理论所有函数都有图像,但是当自变量是无理数时,我们很难画出函数图象。
三、例题练习、巩固理解
例1 画出函数 的图象
解:由绝对值的概念我们有
所以,函数 的图象如右图所示
像例1中这样的函数称为分段函数
追问3:你能通过函数图像看出这个函数的定义域吗?怎样理解分段函数的定义域?
解:由图可知 的定义域为R,所以分段函数的定义域为各段的定义域的并集
三、例题练习、巩固理解
变式训练: 画出函数 的图象
方法1:(描点法)
一、列表
自变量x 0 1 2 3 4
函数值y 2 1 0 1 2
二、描点
二、连线
三、例题练习、巩固理解
变式训练: 画出函数 的图象
方法2:(去绝对值)
解:由绝对值的概念我们有
所以,函数 的图象如右图所示
三、例题练习、巩固理解
变式训练: 画出函数 的图象
方法3:(平移法)
解:由初中所学知识,可知
所以,函数 的图象如右图所示
的图象可由
的图象向右平移两个单位
得到。
例2 给定函数 ,
(1)在同一直角坐标系中画出f(x),g(x)的图像;
(2)用M(x)表示f(x),g(x)中的最大者,记为
M(x)=max{f(x),g(x)}.
例如,当x=2时,M(2)=max{f(2),g(2)} =max{3,9}=9.
请分别用图象法和解析式法表示M(x)
三、例题练习、巩固理解
解:(1)在同一坐标
系中画出f(x),g(x)
的图象如图1所示
(图1)
三、例题练习、巩固理解
解:(2)(方法一)由图1函数取值的情况,结合M(x)的定义,可得M(x)的图象如图2所示,
(图2)
结合图2,
得M(x)的解析式为
例2 给定函数 ,
(2)用M(x)表示f(x),g(x)中的最大者,记为M(x)=
max{f(x),g(x)},请分别用图象法和解析式法表示M(x)
例2 给定函数 ,
(2)用M(x)表示f(x),g(x)中的最大者,记为M(x)=
max{f(x),g(x)}.请分别用图象法和解析式法表示M(x)
三、例题练习、巩固理解
解:(2)(方法二)类比比较数的大小,我们可以用两个函数相减,
得M(x)的解析式为
四、选择方法、情境应用
情境2 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
测试成绩 第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请对这三位同学在高一学年度的数学学习情况做分析.
姓名
解析:从表中可以知道每位同学在每次测试中的成绩,但不容易看出每位同学的成绩的变化情况.可将“成绩”与“测试序号”之间的关系用函数图象表示,如图,可以较直观地看到成绩变化情况.
四、选择方法、情境应用
四、选择方法、情境应用
解析:由图可知王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定.张诚同学成绩不稳定,在班级平均水平上下波动,且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
四、选择方法、情境应用
情境3 依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税)。2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数 ①。应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除 ②。其中,“基本减除费用”(免征额)为每年60000元。税率与速算扣除数见下表。
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1 [0,36 000] 3 0
2 (36 000,144 000] 10 2520
3 (144 000,300 000] 20 16920
4 (300 000,420 000] 25 31920
5 (420 000,660 000] 30 52910
6 (660 000,960 000] 35 85920
7 (960 000,) 45 181920
四、选择方法、情境应用
情境3:(1) 设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图象。
解析: 根据上表,可得函数y=f(t)的解析式为
四、选择方法、情境应用
情境3:(1) 设全年应纳税所得额为t,应缴纳个税税额为y,求 y=f(t),并画出图象。
解析:根据上表,可得函数y=f(t)的图象为
四、选择方法、情境应用
情境3:(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
解析:根据公式②,小王全年应缴纳所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8×189600-117360=34320
将t的值代入③,得
y=0.03×34320=1029.6
所以,小王应缴纳的综合所得个税税额为1029.6元。
五、小结提升、形成结构
学习了本节课,你有什么收获?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
