与三角形有关的角外角[下学期]
文档属性
| 名称 | 与三角形有关的角外角[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-22 23:41:00 | ||
图片预览

文档简介
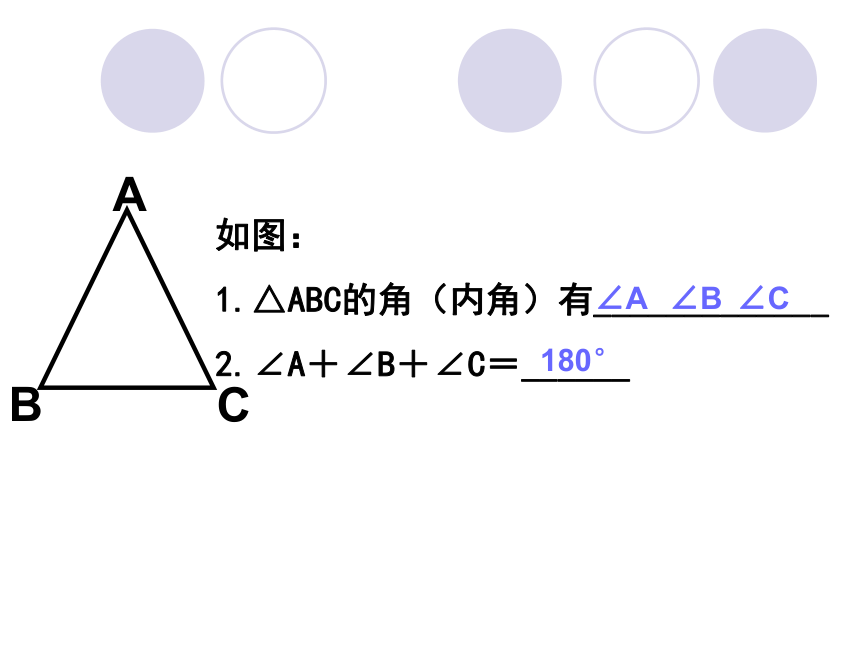
课件25张PPT。7.2.2三角形的外角如图:
1.△ABC的角(内角)有_____________
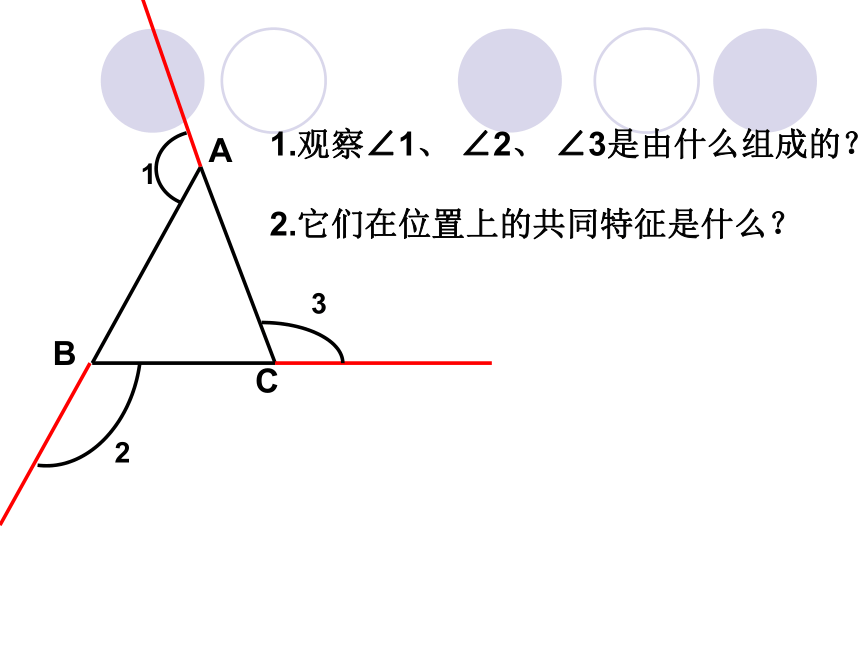
2.∠A+∠B+∠C=______∠A180°∠B∠CABC1.观察∠1、 ∠2、 ∠3是由什么组成的?
2.它们在位置上的共同特征是什么?
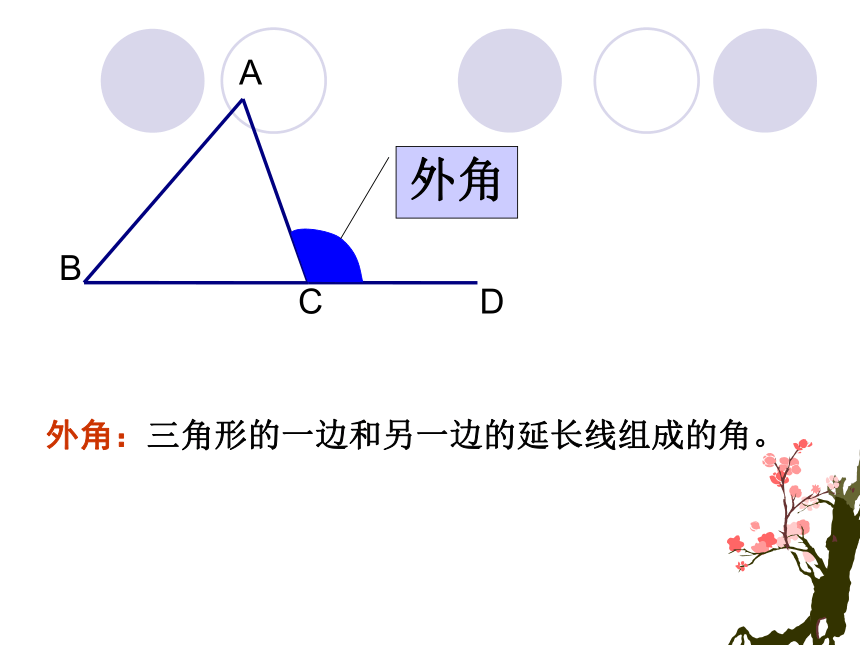
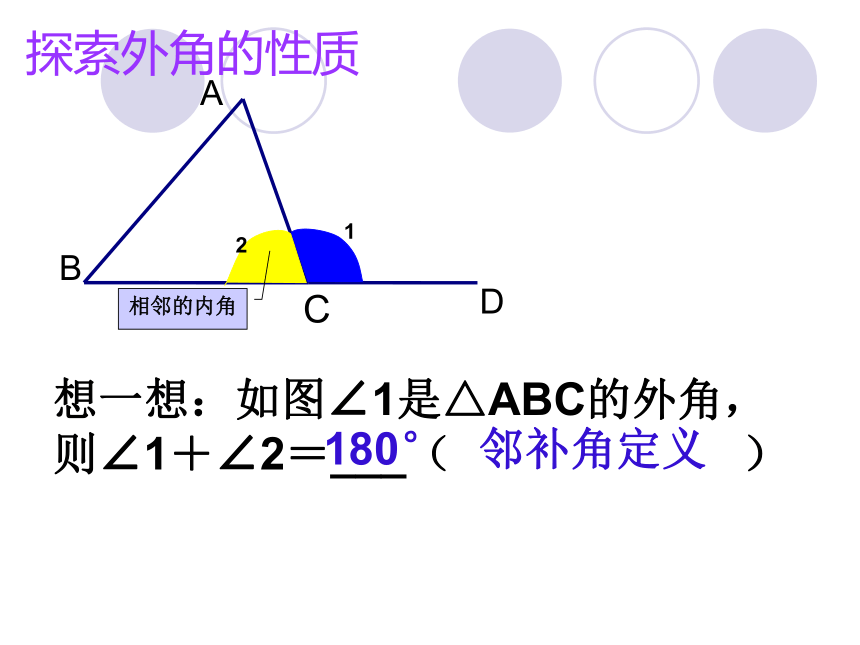
BCA外角外角:三角形的一边和另一边的延长线组成的角。探索外角的性质BA想一想:如图∠1是△ABC的外角,则∠1+∠2=___( )相邻的内角180°邻补角定义C
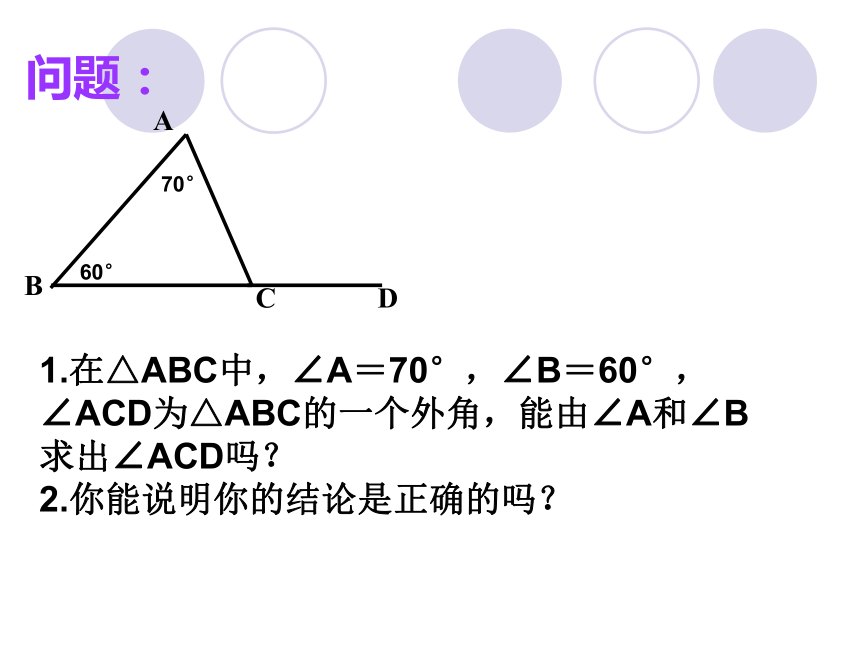
在一张白纸上任意画一个三角形ABC,如图,把∠A、∠B剪下拼在一起,放到∠ACD上,看看会出现什么结果?ABCD动手实践ABCD问题:1.在△ABC中,∠A=70°,∠B=60°,∠ACD为△ABC的一个外角,能由∠A和∠B求出∠ACD吗?
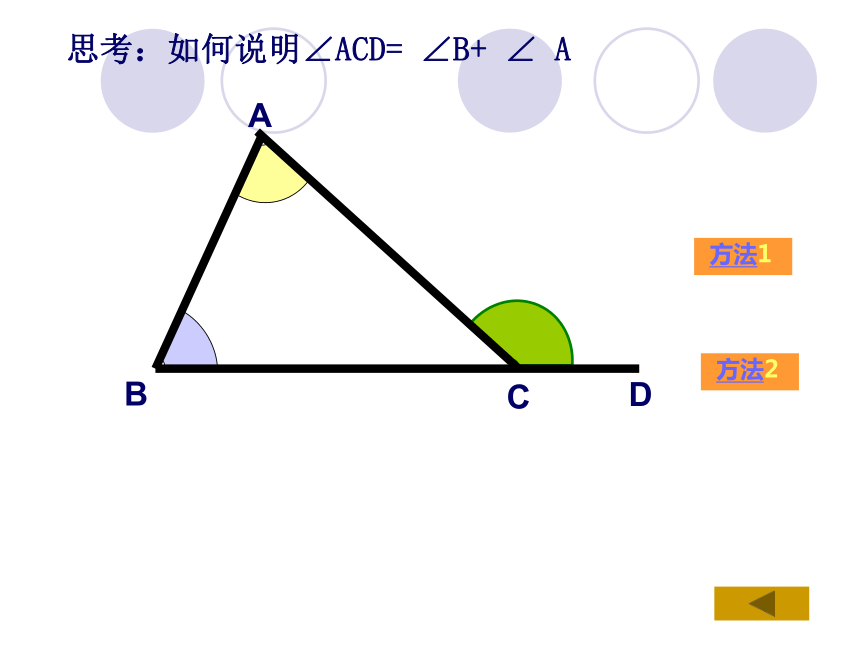
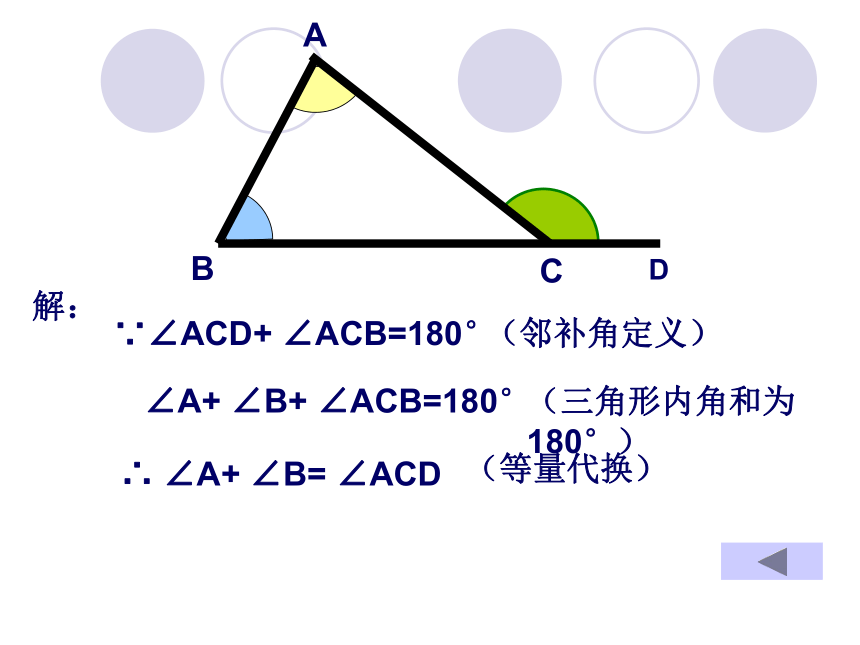
2.你能说明你的结论是正确的吗? 70°60°思考:如何说明∠ACD= ∠B+ ∠ ADD∵∠ACD+ ∠ACB=180° ∠A+ ∠B+ ∠ACB=180°∴ ∠A+ ∠B= ∠ACD解:(邻补角定义)(三角形内角和为180°)(等量代换)D解:过C作CE平行于ABABC∠1= ∠B∠2= ∠A∠1+ ∠2= ∠A+ ∠B即∠ACD= ∠A+ ∠B(两直线平行,同位角相等)(两直线平行,内错角相等)(等式性质)三角形的一个外角等于与它不相邻的两个内角的和。三角形的一个外角与它不相邻的两个内角之间的关系三角形的一个 外角大于任何一个与它不相邻的内角。90o85o95o60o43o30o求下列各图中∠α的度数。试一试综合运用如图AB∥CD,∠A=40°,∠D=45°,求∠1和∠2。ABCD2、这堂课你记忆最深刻的是什么?1、这堂课你最感兴趣的是什么?小结:3、今天你学会了什么?三角形的一个外角的性质(3)三角形的一个外角大于任何一个与它不相邻的内角。(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
国旗上的数学 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数12FG解:∵∠1是△FBE的外角∴∠1=∠B+ ∠E同理∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180oABCDE12F4生活如此美妙!
我们正在拥有!!
一个个奇迹存在于细致的发现之中!!!ABC∠1+∠2+∠3=______
让 我 们 一 起 去 发 现CBOACBOA
1.△ABC的角(内角)有_____________
2.∠A+∠B+∠C=______∠A180°∠B∠CABC1.观察∠1、 ∠2、 ∠3是由什么组成的?
2.它们在位置上的共同特征是什么?
BCA外角外角:三角形的一边和另一边的延长线组成的角。探索外角的性质BA想一想:如图∠1是△ABC的外角,则∠1+∠2=___( )相邻的内角180°邻补角定义C
在一张白纸上任意画一个三角形ABC,如图,把∠A、∠B剪下拼在一起,放到∠ACD上,看看会出现什么结果?ABCD动手实践ABCD问题:1.在△ABC中,∠A=70°,∠B=60°,∠ACD为△ABC的一个外角,能由∠A和∠B求出∠ACD吗?
2.你能说明你的结论是正确的吗? 70°60°思考:如何说明∠ACD= ∠B+ ∠ ADD∵∠ACD+ ∠ACB=180° ∠A+ ∠B+ ∠ACB=180°∴ ∠A+ ∠B= ∠ACD解:(邻补角定义)(三角形内角和为180°)(等量代换)D解:过C作CE平行于ABABC∠1= ∠B∠2= ∠A∠1+ ∠2= ∠A+ ∠B即∠ACD= ∠A+ ∠B(两直线平行,同位角相等)(两直线平行,内错角相等)(等式性质)三角形的一个外角等于与它不相邻的两个内角的和。三角形的一个外角与它不相邻的两个内角之间的关系三角形的一个 外角大于任何一个与它不相邻的内角。90o85o95o60o43o30o求下列各图中∠α的度数。试一试综合运用如图AB∥CD,∠A=40°,∠D=45°,求∠1和∠2。ABCD2、这堂课你记忆最深刻的是什么?1、这堂课你最感兴趣的是什么?小结:3、今天你学会了什么?三角形的一个外角的性质(3)三角形的一个外角大于任何一个与它不相邻的内角。(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
国旗上的数学 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数12FG解:∵∠1是△FBE的外角∴∠1=∠B+ ∠E同理∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180oABCDE12F4生活如此美妙!
我们正在拥有!!
一个个奇迹存在于细致的发现之中!!!ABC∠1+∠2+∠3=______
让 我 们 一 起 去 发 现CBOACBOA
