7.3多边形及其内角和习题[下学期]
文档属性
| 名称 | 7.3多边形及其内角和习题[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 369.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-23 22:37:00 | ||
图片预览


文档简介
课件20张PPT。1、什么是多边形? 在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。2、n边形的内角和是多少?外角和是多少?n边形的内角和等于(n - 2)?180°3、过n边形的某一个顶点的所有对角线有几条?
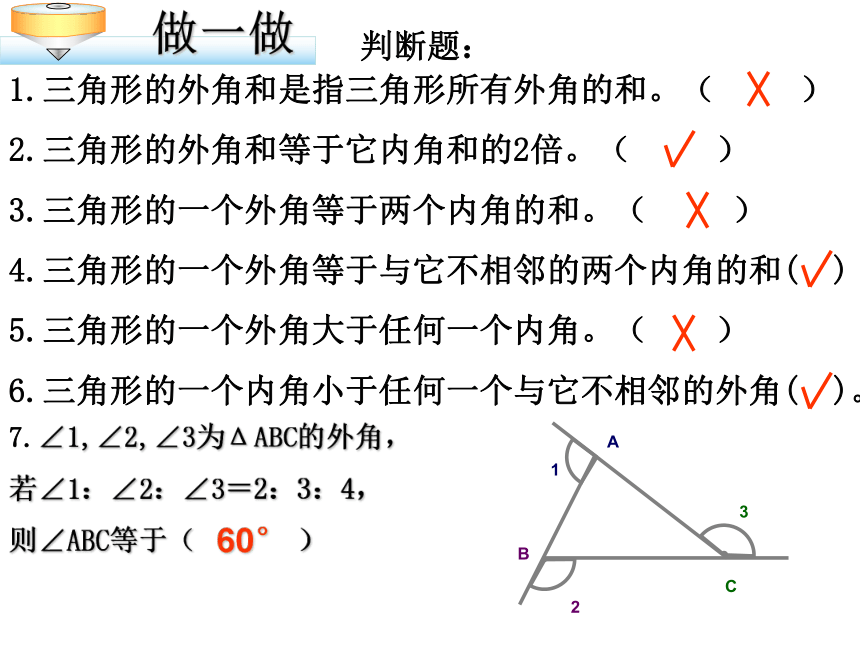
被分成几个三角形?共有几条对角线?有(n - 3) 条。被分成(n - 2) 个三角形。n边形的外角和等于360°判断题:1.三角形的外角和是指三角形所有外角的和。( )
2.三角形的外角和等于它内角和的2倍。( )
3.三角形的一个外角等于两个内角的和。( )
4.三角形的一个外角等于与它不相邻的两个内角的和( )
5.三角形的一个外角大于任何一个内角。( )
6.三角形的一个内角小于任何一个与它不相邻的外角( )。7.∠1,∠2,∠3为ΔABC的外角,
若∠1:∠2:∠3=2:3:4,
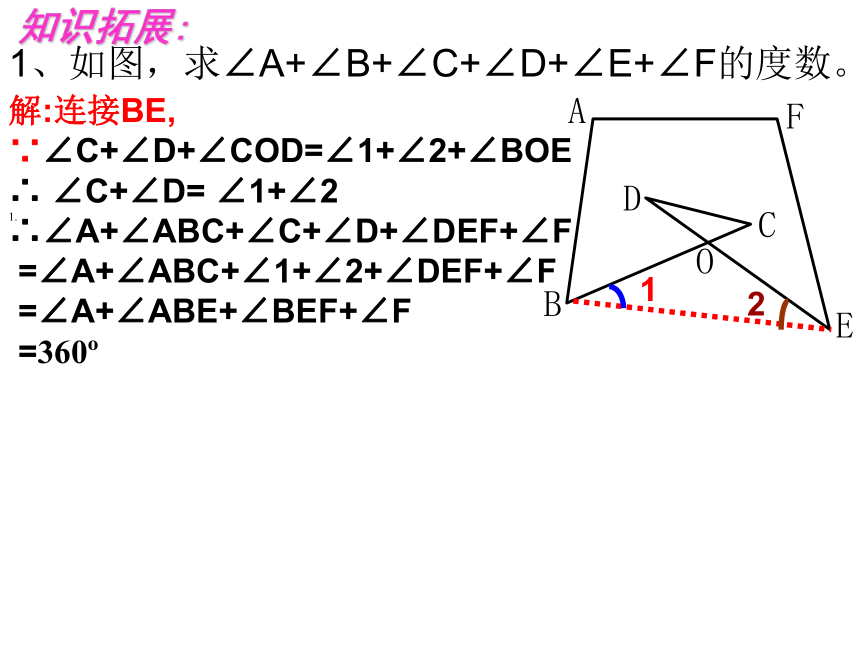
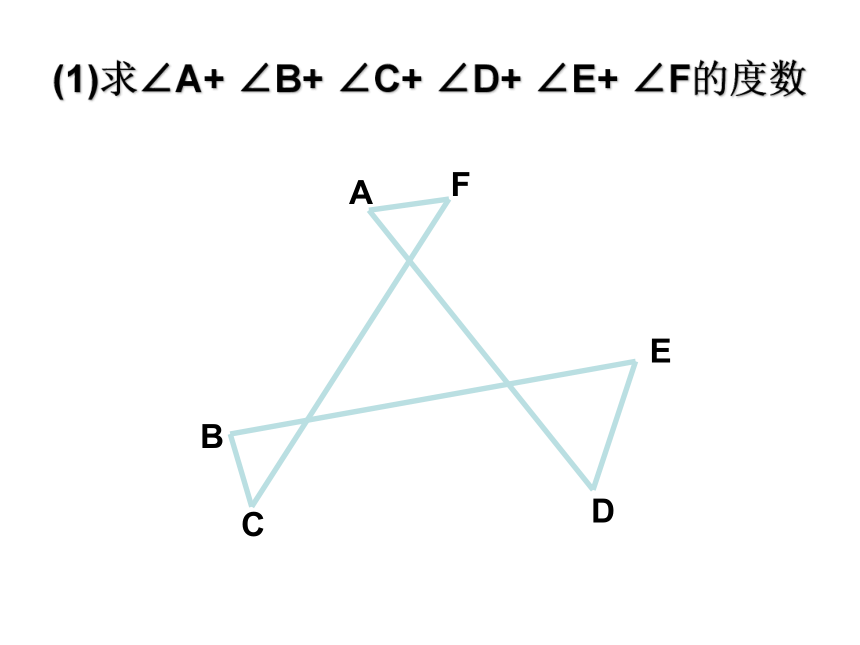
则∠ABC等于( )60°1、如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数。 1.????????
知识拓展:12解:连接BE,
∵∠C+∠D+∠COD=∠1+∠2+∠BOE
∴ ∠C+∠D= ∠1+∠2
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360o
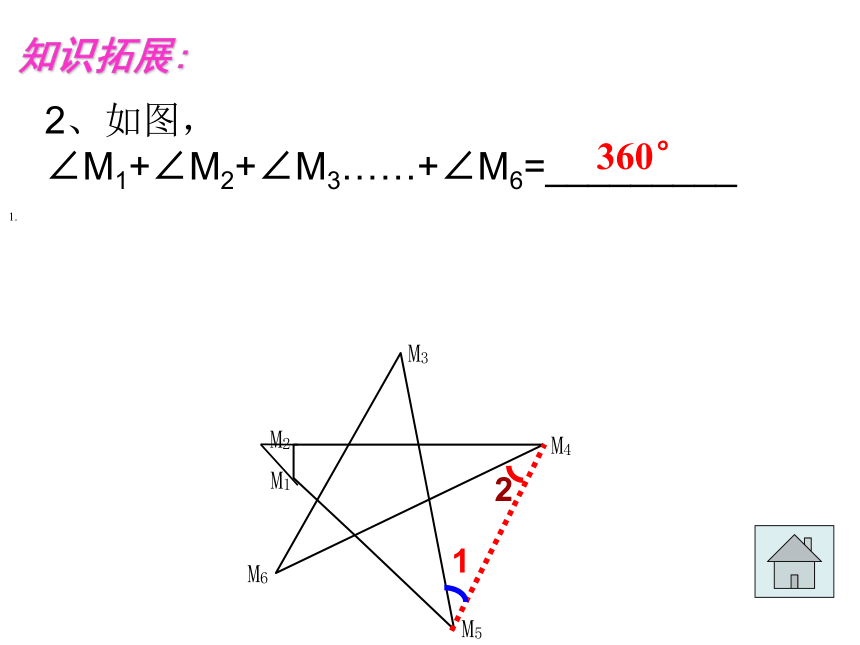
2、如图,∠M1+∠M2+∠M3……+∠M6=_________
1.????????
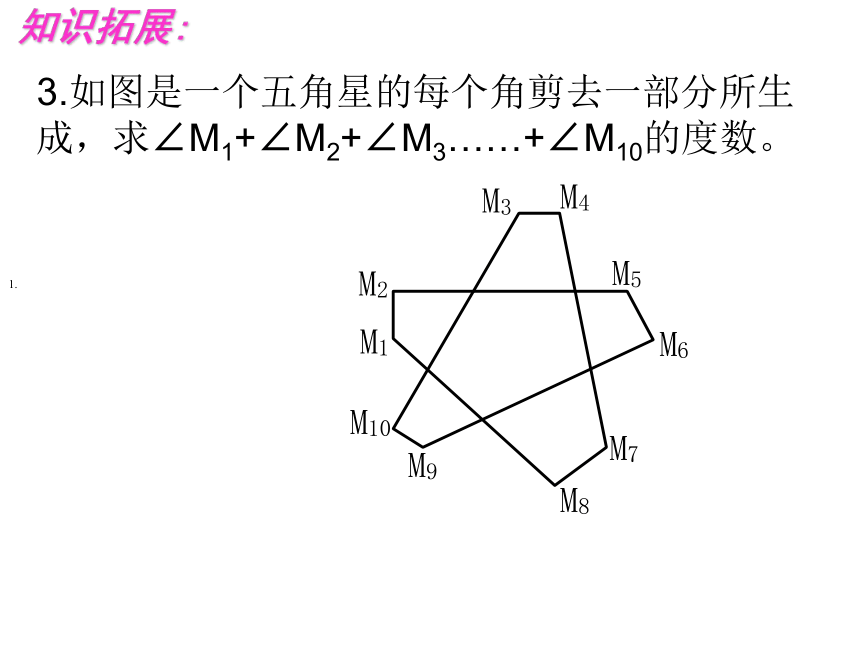
知识拓展:360°123.如图是一个五角星的每个角剪去一部分所生成,求∠M1+∠M2+∠M3……+∠M10的度数。 1.????????
知识拓展:
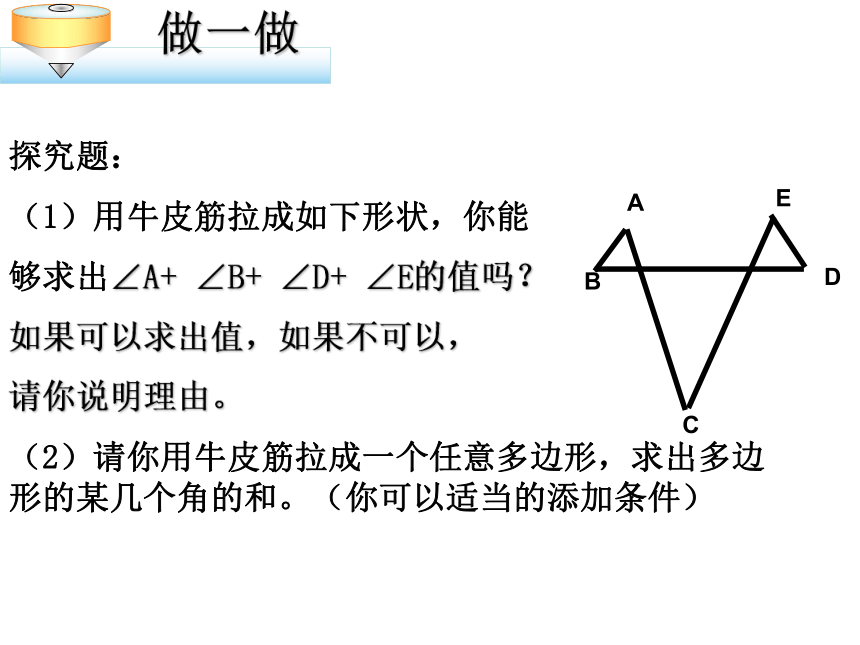
探究题:
(1)用牛皮筋拉成如下形状,你能
够求出∠A+ ∠B+ ∠D+ ∠E的值吗?
如果可以求出值,如果不可以,
请你说明理由。
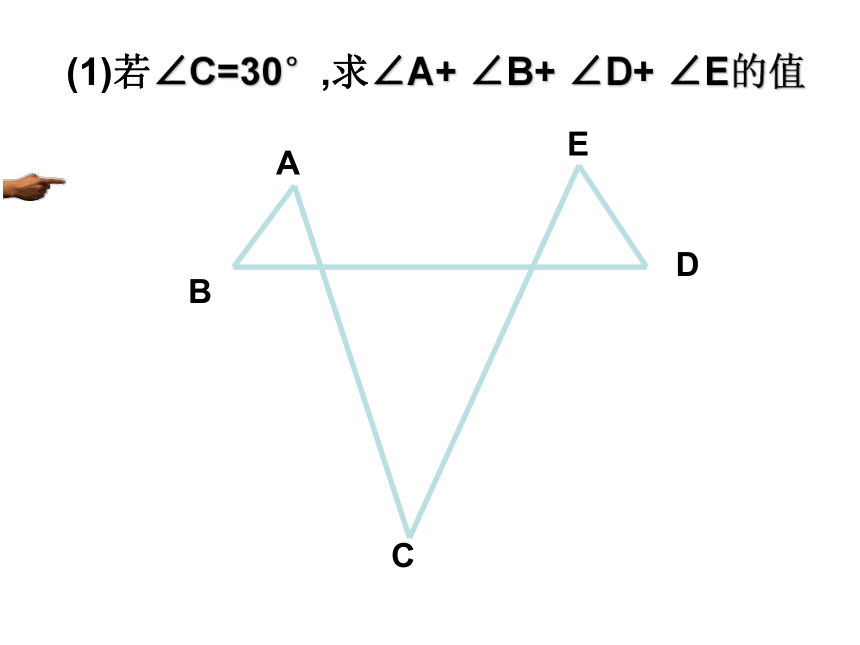
(2)请你用牛皮筋拉成一个任意多边形,求出多边形的某几个角的和。(你可以适当的添加条件)(1)若∠C=30°,求∠A+ ∠B+ ∠D+ ∠E的值(1)求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数你可以想出多少种方法计算:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。例1:如图D是ΔABC中AC边上一点,∠C=∠DBC,
若∠BDA=80°,∠ABC=70°,求∠A;∠C度数。解:∵ ∠BDA是△BCD的外角
∴∠BDC+∠C=∠BDA= 80°
而∠C=∠DBC
∴∠C= 40°
∵ ∠ABC= 70°
∴∠A= 180° -∠ABC- ∠C
= 180°-70°- 80°
= 70°
(1)4x+ 60=(5-2)×180
解得x=120(2)3x+3x+2x+4x=(4-2) ×180
解得x=30
180°360°540°720°1080°1800°360°360°360°360°360°360°3.填空:解:五边形的内角和=(5-2)× 180°= 540°
正五边形的每个内角是540°?5= 108°
十边形的内角和=(10-2)× 180°= 1440°
正十边形的每个内角是1440°?10= 144°九边形(1)三角形(2)六边形解:∵∠A+∠B+∠C+∠D= 360°
∠A=∠C, ∠B=∠D
∴ ∠A+∠D+∠A+∠D= 360°
∠A+∠D= 180°
∴ AB∥CD
同理可得 BC∥AD
解(1)∵BC⊥CD ∴ ∠BCD= 90°
∴ ∠1+∠2= 90°,而∠1=∠2=∠3,
∴ ∠1= ∠ 2=∠3= 45°
在△COD中, ∠COD= 180°- ∠1-∠3= 90°
∴CO是△BCD的高.
(2) ∵ ∠COD= 90°, ∠4= 60°
∴ ∠5= 90°- ∠4= 30°
(3)∵ ∠5= 30°, ∠5= ∠6 ∴ ∠DAB= ∠5+∠6= 60°
在△ABD中, ∠ABD= 180°- ∠4-∠DAB= 60°
∴ ∠ABC= ∠2+∠ABD=45°+ 60°=105°
∠BCD= 90°, ∠ADC= ∠1+∠4= 45°+ 60°=105°
解:五边形的内角和=(5-2)× 180°= 540°
∵五边形ABCDE的内角都相等,
∴∠CDE= ∠ E=∠C= 108°.
∵ ∠1+∠2+∠E= 180°, ∠ 1=∠2
∴∠1= ∠ 2= 36°
同理可得∠3= ∠ 4= 36°.
∴∠ADB= ∠CDE-∠1- ∠3
= 108°-36°- 36°
= 36°
即x= 36°
解:六边形的内角和=(6-2)× 180°= 720°
∵六边形ABCDEF的内角都相等,
∴∠CDE= ∠ B=∠C= ∠E=120°.
在四边形ABCD中,
∠ADC= 360°- ∠DAB-∠B- ∠C
= 360°- 60°-120°- 120°= 60°
∴∠ADE= ∠CDE-∠ADC= 120°- 60° =60°
∴ ∠DAB = ∠ADE ∴ AB∥DE
∵ ∠DAB+∠B= 60°+ 120° =180°∴ BC∥AD
∵ ∠ADE+∠E= 60°+ 120° =180°∴ EF∥AD
∴ BC∥EF
学具——每种正多边形各六个正六边形正八边形正十边形正十二边形正五边形谢谢再见
下课
被分成几个三角形?共有几条对角线?有(n - 3) 条。被分成(n - 2) 个三角形。n边形的外角和等于360°判断题:1.三角形的外角和是指三角形所有外角的和。( )
2.三角形的外角和等于它内角和的2倍。( )
3.三角形的一个外角等于两个内角的和。( )
4.三角形的一个外角等于与它不相邻的两个内角的和( )
5.三角形的一个外角大于任何一个内角。( )
6.三角形的一个内角小于任何一个与它不相邻的外角( )。7.∠1,∠2,∠3为ΔABC的外角,
若∠1:∠2:∠3=2:3:4,
则∠ABC等于( )60°1、如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数。 1.????????
知识拓展:12解:连接BE,
∵∠C+∠D+∠COD=∠1+∠2+∠BOE
∴ ∠C+∠D= ∠1+∠2
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360o
2、如图,∠M1+∠M2+∠M3……+∠M6=_________
1.????????
知识拓展:360°123.如图是一个五角星的每个角剪去一部分所生成,求∠M1+∠M2+∠M3……+∠M10的度数。 1.????????
知识拓展:
探究题:
(1)用牛皮筋拉成如下形状,你能
够求出∠A+ ∠B+ ∠D+ ∠E的值吗?
如果可以求出值,如果不可以,
请你说明理由。
(2)请你用牛皮筋拉成一个任意多边形,求出多边形的某几个角的和。(你可以适当的添加条件)(1)若∠C=30°,求∠A+ ∠B+ ∠D+ ∠E的值(1)求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数你可以想出多少种方法计算:
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。例1:如图D是ΔABC中AC边上一点,∠C=∠DBC,
若∠BDA=80°,∠ABC=70°,求∠A;∠C度数。解:∵ ∠BDA是△BCD的外角
∴∠BDC+∠C=∠BDA= 80°
而∠C=∠DBC
∴∠C= 40°
∵ ∠ABC= 70°
∴∠A= 180° -∠ABC- ∠C
= 180°-70°- 80°
= 70°
(1)4x+ 60=(5-2)×180
解得x=120(2)3x+3x+2x+4x=(4-2) ×180
解得x=30
180°360°540°720°1080°1800°360°360°360°360°360°360°3.填空:解:五边形的内角和=(5-2)× 180°= 540°
正五边形的每个内角是540°?5= 108°
十边形的内角和=(10-2)× 180°= 1440°
正十边形的每个内角是1440°?10= 144°九边形(1)三角形(2)六边形解:∵∠A+∠B+∠C+∠D= 360°
∠A=∠C, ∠B=∠D
∴ ∠A+∠D+∠A+∠D= 360°
∠A+∠D= 180°
∴ AB∥CD
同理可得 BC∥AD
解(1)∵BC⊥CD ∴ ∠BCD= 90°
∴ ∠1+∠2= 90°,而∠1=∠2=∠3,
∴ ∠1= ∠ 2=∠3= 45°
在△COD中, ∠COD= 180°- ∠1-∠3= 90°
∴CO是△BCD的高.
(2) ∵ ∠COD= 90°, ∠4= 60°
∴ ∠5= 90°- ∠4= 30°
(3)∵ ∠5= 30°, ∠5= ∠6 ∴ ∠DAB= ∠5+∠6= 60°
在△ABD中, ∠ABD= 180°- ∠4-∠DAB= 60°
∴ ∠ABC= ∠2+∠ABD=45°+ 60°=105°
∠BCD= 90°, ∠ADC= ∠1+∠4= 45°+ 60°=105°
解:五边形的内角和=(5-2)× 180°= 540°
∵五边形ABCDE的内角都相等,
∴∠CDE= ∠ E=∠C= 108°.
∵ ∠1+∠2+∠E= 180°, ∠ 1=∠2
∴∠1= ∠ 2= 36°
同理可得∠3= ∠ 4= 36°.
∴∠ADB= ∠CDE-∠1- ∠3
= 108°-36°- 36°
= 36°
即x= 36°
解:六边形的内角和=(6-2)× 180°= 720°
∵六边形ABCDEF的内角都相等,
∴∠CDE= ∠ B=∠C= ∠E=120°.
在四边形ABCD中,
∠ADC= 360°- ∠DAB-∠B- ∠C
= 360°- 60°-120°- 120°= 60°
∴∠ADE= ∠CDE-∠ADC= 120°- 60° =60°
∴ ∠DAB = ∠ADE ∴ AB∥DE
∵ ∠DAB+∠B= 60°+ 120° =180°∴ BC∥AD
∵ ∠ADE+∠E= 60°+ 120° =180°∴ EF∥AD
∴ BC∥EF
学具——每种正多边形各六个正六边形正八边形正十边形正十二边形正五边形谢谢再见
下课
