人教版七年级上册 1.5.1 乘方课件(共34张PPT)
文档属性
| 名称 | 人教版七年级上册 1.5.1 乘方课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1014.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 23:05:55 | ||
图片预览








文档简介
(共34张PPT)
有理数的乘方
边长为3的正方形 的面积是______.
3×3可以记作___, 读作_________.
3
3
3×3
32
3的平方
9
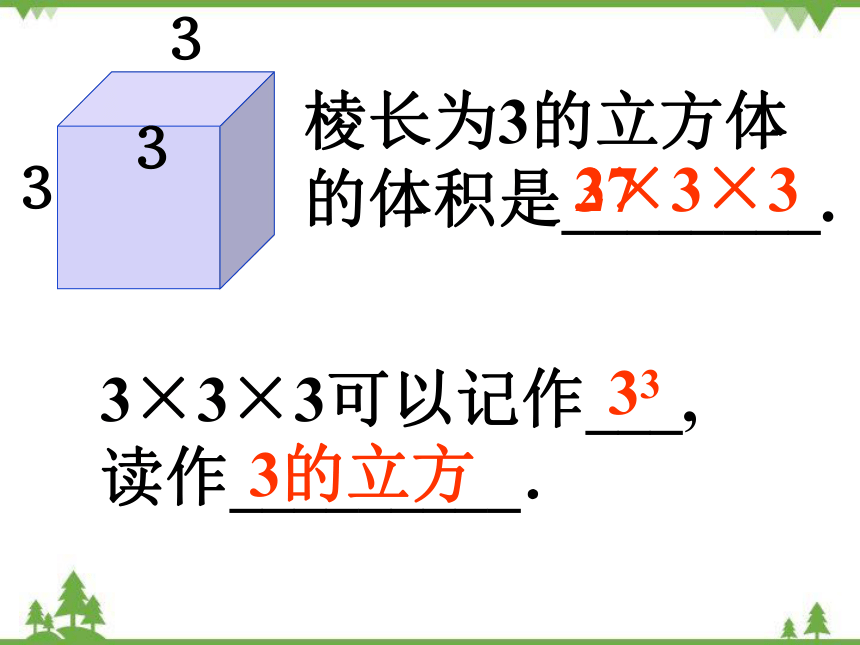
棱长为3的立方体 的体积是________.
3×3×3可以记作___, 读作_________.
3
3
3
3×3×3
33
3的立方
27
3
3
3
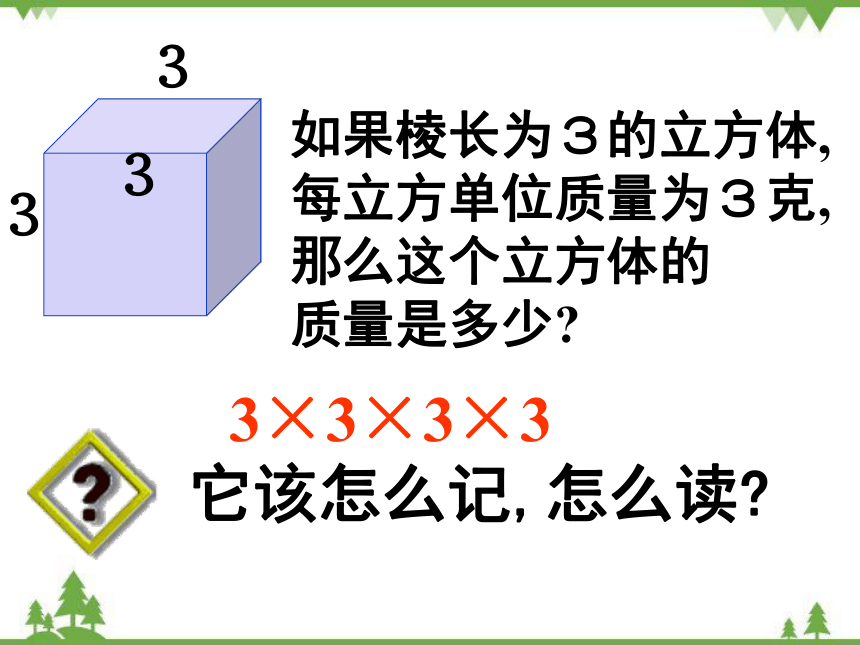
如果棱长为3的立方体, 每立方单位质量为3克, 那么这个立方体的 质量是多少
它该怎么记,怎么读
3×3×3×3
活动要求:把一张纸进行对折、再对折……并作记录(两人合作)问题:
(1)对折一次有几层
(2)对折二次有几层
(3)对折三次有几层
(4)对折四次有几层
……
2
4
8
16
2×2
2×2 ×2
2×2 ×2×2
2
=2
=22
=23
=24
2×2 ×2 ··· ×2
n个
= 2n
做一做,议一议
(5)对折n次有几层
太好了!
乘方的意义
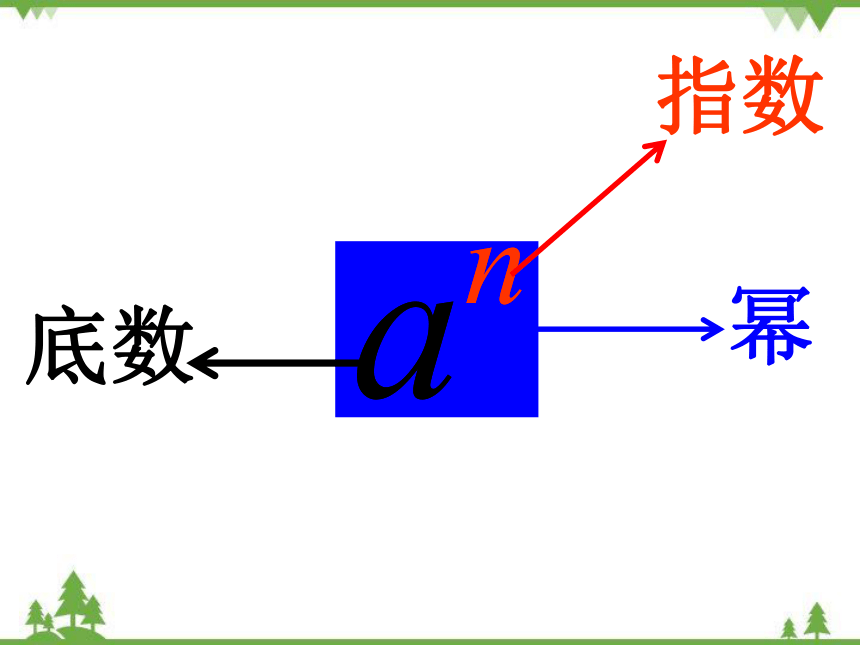
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂(power),在an中,a叫做底数,n叫做指数.
获取新知
a×a ×a ··· ×a
n个
= an
an读作a的n次幂(或a的n次方).
底数
指数
幂
n
a
n
a
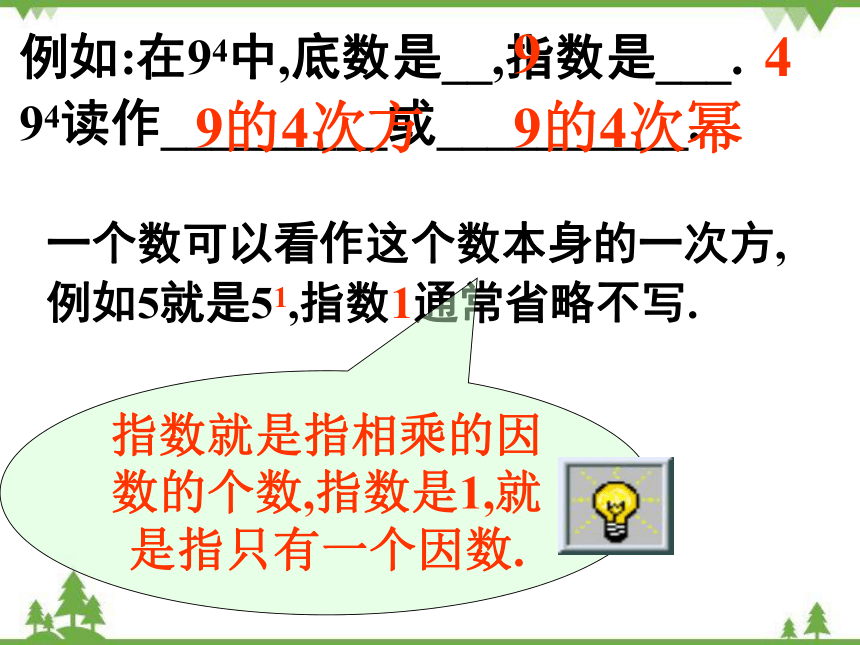
例如:在94中,底数是__,指数是___.
94读作_________或__________.
9
4
9的4次方
9的4次幂
一个数可以看作这个数本身的一次方,例如5就是51,指数1通常省略不写.
指数就是指相乘的因数的个数,指数是1,就是指只有一个因数.
( 1)23中底数是 ,指数是 .
(2)在 中底数是 ,指数是 .
(3)在8中底数是 ,指数是 .
练一练
2
3
2
8
1
真棒!
真不错!
你真行!
给自己一个机会
把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2.(-1.3)(-1.3)(-1.3)(-1.3)(-1.3)
3.
4.
=55
= (-1.3) 5
= m 2a
很好!
不错!
例1.计算:(1) ①23;②33;③43;④24;
(2) ①(-2)3;② (-3)3 ; ③(-4)3;④ (-2)5;
(3) ①(-2)2;② (-3)2 ; ③(-4)2;④ (-2)4;
因为an就是n个a相乘,所以可以利用有理数的乘法运算进行有理数的乘方运算.
例1.解:
(1)
①23= ;
②33= ;
③43= ;
④24= ;
(2) ①(-2)3= ; ②(-3)3= ; ③(-4)3= ; ④(-2)5= ;
(3) ①(-2)2 = ; ②(-3)2 = ; ③(-4)2 = ; ④(-2)4 = ;
8
27
64
16
-8
-27
-64
-32
4
9
16
16
观察此例题,你发现了什么规律
一个正数的任何次幂都是___数;
正
一个负数的偶次幂是__数,奇次幂是__数.
正
负
太棒了!
判断下列各幂是正的还是负的
(1) (-7)9
(2) (-3)6
(3) (-1)101
正
负
负
负
正
(5) (-2)4
正
(4)
(6)
负
(7) -(-2)4
负
(8) -24
你答的真好!
1. 53; 2. ;
3. ; 4. (-3)2 ;
5. -32; 6. 0100.
我能行,我最棒
0的任何正整数次幂都是0
我做的最快!
计算:
注意:(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来.
(3)(-2)4和-24的不同:
(-2)4读作-2的4次幂(或-2的4次方), (-2)4的底数是-2,指数是4,结果为正.
而-24读作2的4次幂的相反数(或2的4次方的相反数), -24的底数是2,指数是4,结果为负.
1、判断下列各题是否正确
① 23=2 ×3 ( )
② 2+2+2=23 ( )
③ 23=2×2 ×2 ( )
×
√
×
火眼金睛
Very Good!
题目 底数的符号 指数的奇、偶 幂的符号
32
53
(-3)4
(-2)6
(-3)3
(-4)5
+
+
-
-
-
-
+
+
+
+
-
-
奇
奇
奇
偶
偶
偶
①正数的任何次幂都是___数;
②负数的奇次幂是___数,
负数的偶次幂是___数;
③0的任何正整数次幂是__.
正
负
正
0
通过练习思考归纳乘方的法则
例2:计算
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1000
=10000
=100
=-1000
=10000
想一想:观察例2的结果,你又能发现什么规律
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
收获知多少
1.求n个相同因数的积的运算叫______,积的结果叫做___,相同因数的个数叫做_____.
2.求乘方的方法是用_____运算. .
3.乘方的运算法则是:
乘方
幂
指数
乘法
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂是0.
4.如果a、b互为相反数,那么
a2n=b2n,a2n+1+b2n+1=0 .
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
(1) (-2)5 (6) -(-1)101
(4) (-0.1)3 (9)-12007
(2) (-10)5 (7) (-3)3
(3) (-1)20 (8) -33
(5) 12006 (10)
小测验
我能行
1米长的小棒,第一次截去一半,第2次截去剩下的一半,如此下去,第5次后剩下的小棒有多长
牛刀小试
你真是个
聪明孩子
→
→
→
→
…
你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,把两头捏合在一起,再捏合,再拉伸,反复几次,就把一根很粗的面条拉成了许多细的面条,如下面的草图所示:
求捏合到多少次后可拉出128根细面条
上拉面
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个
细胞分裂
细胞分裂示意图
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844.43米.
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰.这是真的吗
学以致用
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格.”“你真傻!就要这么一点米 ”,国王哈哈大笑.这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗
棋盘上的学问
推荐作业可以通过查资料,借助计算器,估算……
把分析的过程和理由写在数学成长日记本上,下午交上!
作业友情提示
作业:课本第47页习题1.5第1题;
推荐作业:1.山西有一位拉面大王,他能把一斤面粉和成面团,再捏合多次拉成1000多根拉面条,拉面他必须保证至少拉几次还不断
2.折30次纸的高度能超过珠穆朗玛峰的高度吗
3.你认为国王的国库里有这么多米吗
End
作业
有一个含8×8=64个方格的正方形
棋盘.在第一个格里放有一枚硬币,在第二
个格里放有2枚硬币,在第三个格里放有4
枚硬币……,以此类推,每一个格里的硬
币数总是前一个格里的硬币数的2倍.并且
每枚硬币的厚度都是2毫米.请你猜一猜,
第64个格里的硬币摞成一摞有多高 1米
100米 1000米 肯定不对!它是一个
可怕的天文数字!
264有多大
它不就是264毫米高吗 有什么值得大惊小怪的!可是,你知道吗 把这个数用10进制有理
数表示出来,它就是:
264毫米=184467.44073709551616亿千米.
如果按照264毫米的尺寸做一架木制梯子.再
把它锯成长度相等的十二万三千三百零七段,
你知道截断的每一小段梯子有什么用吗 把它
立起来,沿着它可以爬到太阳上去!而且等你
登上太阳的时候,立刻会发现这一小段梯子还
多出137千米没用着!因为它的长度是
49600137千米,而太阳离地球的距离为
49600000千米.
这个数好大啊!
学习是件很愉快的事:既学到了知识,又长了见识;既让别人重新认识,又得到他人的赏识.
同学们学的很认真
望继续努力
谢谢合作
祝同学们学习愉快
有理数的乘方
边长为3的正方形 的面积是______.
3×3可以记作___, 读作_________.
3
3
3×3
32
3的平方
9
棱长为3的立方体 的体积是________.
3×3×3可以记作___, 读作_________.
3
3
3
3×3×3
33
3的立方
27
3
3
3
如果棱长为3的立方体, 每立方单位质量为3克, 那么这个立方体的 质量是多少
它该怎么记,怎么读
3×3×3×3
活动要求:把一张纸进行对折、再对折……并作记录(两人合作)问题:
(1)对折一次有几层
(2)对折二次有几层
(3)对折三次有几层
(4)对折四次有几层
……
2
4
8
16
2×2
2×2 ×2
2×2 ×2×2
2
=2
=22
=23
=24
2×2 ×2 ··· ×2
n个
= 2n
做一做,议一议
(5)对折n次有几层
太好了!
乘方的意义
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂(power),在an中,a叫做底数,n叫做指数.
获取新知
a×a ×a ··· ×a
n个
= an
an读作a的n次幂(或a的n次方).
底数
指数
幂
n
a
n
a
例如:在94中,底数是__,指数是___.
94读作_________或__________.
9
4
9的4次方
9的4次幂
一个数可以看作这个数本身的一次方,例如5就是51,指数1通常省略不写.
指数就是指相乘的因数的个数,指数是1,就是指只有一个因数.
( 1)23中底数是 ,指数是 .
(2)在 中底数是 ,指数是 .
(3)在8中底数是 ,指数是 .
练一练
2
3
2
8
1
真棒!
真不错!
你真行!
给自己一个机会
把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2.(-1.3)(-1.3)(-1.3)(-1.3)(-1.3)
3.
4.
=55
= (-1.3) 5
= m 2a
很好!
不错!
例1.计算:(1) ①23;②33;③43;④24;
(2) ①(-2)3;② (-3)3 ; ③(-4)3;④ (-2)5;
(3) ①(-2)2;② (-3)2 ; ③(-4)2;④ (-2)4;
因为an就是n个a相乘,所以可以利用有理数的乘法运算进行有理数的乘方运算.
例1.解:
(1)
①23= ;
②33= ;
③43= ;
④24= ;
(2) ①(-2)3= ; ②(-3)3= ; ③(-4)3= ; ④(-2)5= ;
(3) ①(-2)2 = ; ②(-3)2 = ; ③(-4)2 = ; ④(-2)4 = ;
8
27
64
16
-8
-27
-64
-32
4
9
16
16
观察此例题,你发现了什么规律
一个正数的任何次幂都是___数;
正
一个负数的偶次幂是__数,奇次幂是__数.
正
负
太棒了!
判断下列各幂是正的还是负的
(1) (-7)9
(2) (-3)6
(3) (-1)101
正
负
负
负
正
(5) (-2)4
正
(4)
(6)
负
(7) -(-2)4
负
(8) -24
你答的真好!
1. 53; 2. ;
3. ; 4. (-3)2 ;
5. -32; 6. 0100.
我能行,我最棒
0的任何正整数次幂都是0
我做的最快!
计算:
注意:(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来.
(3)(-2)4和-24的不同:
(-2)4读作-2的4次幂(或-2的4次方), (-2)4的底数是-2,指数是4,结果为正.
而-24读作2的4次幂的相反数(或2的4次方的相反数), -24的底数是2,指数是4,结果为负.
1、判断下列各题是否正确
① 23=2 ×3 ( )
② 2+2+2=23 ( )
③ 23=2×2 ×2 ( )
×
√
×
火眼金睛
Very Good!
题目 底数的符号 指数的奇、偶 幂的符号
32
53
(-3)4
(-2)6
(-3)3
(-4)5
+
+
-
-
-
-
+
+
+
+
-
-
奇
奇
奇
偶
偶
偶
①正数的任何次幂都是___数;
②负数的奇次幂是___数,
负数的偶次幂是___数;
③0的任何正整数次幂是__.
正
负
正
0
通过练习思考归纳乘方的法则
例2:计算
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1000
=10000
=100
=-1000
=10000
想一想:观察例2的结果,你又能发现什么规律
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
收获知多少
1.求n个相同因数的积的运算叫______,积的结果叫做___,相同因数的个数叫做_____.
2.求乘方的方法是用_____运算. .
3.乘方的运算法则是:
乘方
幂
指数
乘法
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂是0.
4.如果a、b互为相反数,那么
a2n=b2n,a2n+1+b2n+1=0 .
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
(1) (-2)5 (6) -(-1)101
(4) (-0.1)3 (9)-12007
(2) (-10)5 (7) (-3)3
(3) (-1)20 (8) -33
(5) 12006 (10)
小测验
我能行
1米长的小棒,第一次截去一半,第2次截去剩下的一半,如此下去,第5次后剩下的小棒有多长
牛刀小试
你真是个
聪明孩子
→
→
→
→
…
你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,把两头捏合在一起,再捏合,再拉伸,反复几次,就把一根很粗的面条拉成了许多细的面条,如下面的草图所示:
求捏合到多少次后可拉出128根细面条
上拉面
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个
细胞分裂
细胞分裂示意图
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844.43米.
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰.这是真的吗
学以致用
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格.”“你真傻!就要这么一点米 ”,国王哈哈大笑.这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗
棋盘上的学问
推荐作业可以通过查资料,借助计算器,估算……
把分析的过程和理由写在数学成长日记本上,下午交上!
作业友情提示
作业:课本第47页习题1.5第1题;
推荐作业:1.山西有一位拉面大王,他能把一斤面粉和成面团,再捏合多次拉成1000多根拉面条,拉面他必须保证至少拉几次还不断
2.折30次纸的高度能超过珠穆朗玛峰的高度吗
3.你认为国王的国库里有这么多米吗
End
作业
有一个含8×8=64个方格的正方形
棋盘.在第一个格里放有一枚硬币,在第二
个格里放有2枚硬币,在第三个格里放有4
枚硬币……,以此类推,每一个格里的硬
币数总是前一个格里的硬币数的2倍.并且
每枚硬币的厚度都是2毫米.请你猜一猜,
第64个格里的硬币摞成一摞有多高 1米
100米 1000米 肯定不对!它是一个
可怕的天文数字!
264有多大
它不就是264毫米高吗 有什么值得大惊小怪的!可是,你知道吗 把这个数用10进制有理
数表示出来,它就是:
264毫米=184467.44073709551616亿千米.
如果按照264毫米的尺寸做一架木制梯子.再
把它锯成长度相等的十二万三千三百零七段,
你知道截断的每一小段梯子有什么用吗 把它
立起来,沿着它可以爬到太阳上去!而且等你
登上太阳的时候,立刻会发现这一小段梯子还
多出137千米没用着!因为它的长度是
49600137千米,而太阳离地球的距离为
49600000千米.
这个数好大啊!
学习是件很愉快的事:既学到了知识,又长了见识;既让别人重新认识,又得到他人的赏识.
同学们学的很认真
望继续努力
谢谢合作
祝同学们学习愉快
