镶嵌[下学期]

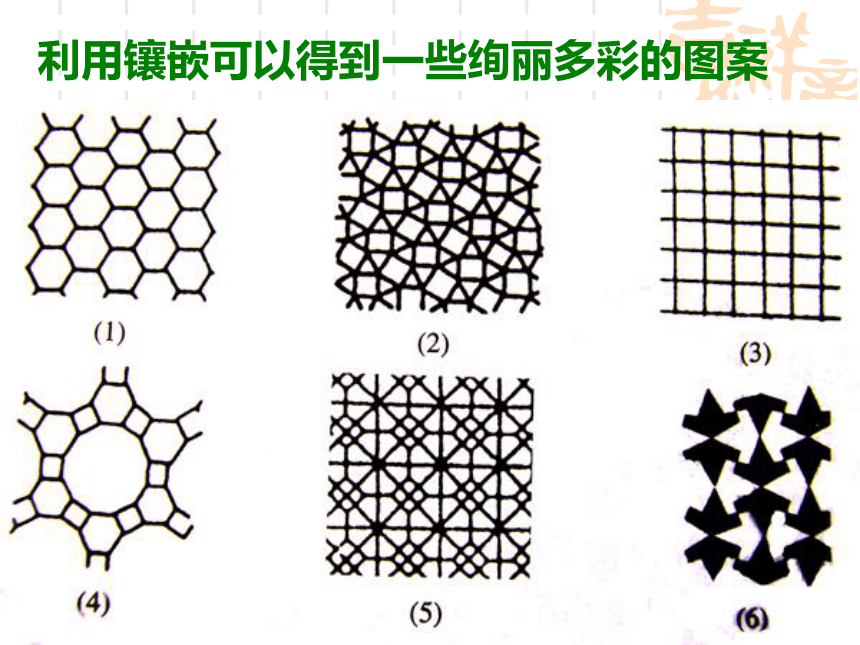
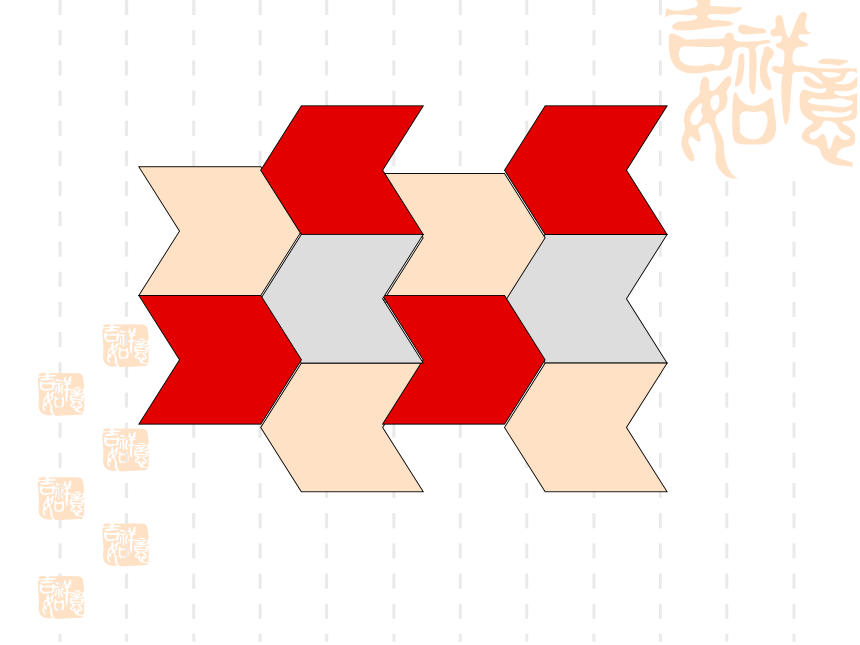
课件27张PPT。 好漂亮的地板!这是怎么铺设的?一点空隙也没有. 我们经常能见到各种建筑物的地板，观察地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案7.4 课题学习 镶嵌利用镶嵌可以得到一些绚丽多彩的图案 用一些形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地把平面的一部分完全覆盖，这就是平面图形的镶嵌．
注意：各种图形拼接后要既无缝隙，又不重叠做一做 （1）用边长相同的正三角形能否镶嵌？结论：用边长相同的正三角形可以镶嵌（2）用边长相同的正方形能否镶嵌？结论：用边长相同的正方形可以镶嵌（4）用边长相同的正六边形能否镶嵌？结论：用边长相同的正六边形可以镶嵌啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?（3）用边长相同的正五边形能否镶嵌？一、用一种正多边形镶嵌平面特征：围绕一点拼在一起的几个正多边形的内角加在一起，恰好是360度（周角）。思考：边长相同的正八边形能镶嵌平面吗？正九边形呢？60x6=360o108x3<360o
108x4>360o120x3=360o135x2<360o
135x3>360o140x2<360o
140x3>360o135o 140o90x4＝360o 要用正多边形镶嵌成一个平面的关键是看：这种正多边形的一个内角的倍数是否是360° 在正多边形里，正三角形的每个内角都是60°，正四边形的每个内角都是90°，正六边形的每个内角都是120°， 这三种多边形的一个内角的倍数都是360°，而其他的正多边形的每个内角的倍数都不是360°所以说：在正多边形里只有正三角形、正四边形、正六边形可以镶嵌，而其他的正多边形不可镶嵌．你还能找到能镶嵌的其他正多边形吗？我们可以利用多边形设计一些美丽的图案．问题用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?二、用多种正多边形镶嵌平面问1：用边长相同的正三角形与正方形能镶嵌吗？60o x 3 ＋ 90o x 2 = 360o问2：用边长相同的正四边形、正六边形和正十二边形能镶嵌平面吗？能！90ox 1＋ 120o x 1 ＋ 150o x 1 ＝ 360o结论：拼接在同一个点的各个角的和，恰好等于360度，就能镶嵌平面。3)正五边形与正十边形1)正四边形与正八边形4)正三角形与正十二边形2)正三边形、正四边形
与正六边形课堂小结 本节课我们通过活动，探讨，知道任意一个三角形，四边形或正六边形可以镶嵌成一个平面，并且探索出正多边形镶嵌的条件．即：一种正多边形的一个内角的倍数是否是360°
作业: 请同学搜集一些平面镶嵌图案,用硬纸片做出其中的一二个模型.小 结 S h u x u e台州市书生中学朱仁江制作再 见