初中数学苏科版(新版)八年级下9.4矩形菱形正方形 第3课时 正方形 课件(共32张PPT)
文档属性
| 名称 | 初中数学苏科版(新版)八年级下9.4矩形菱形正方形 第3课时 正方形 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1004.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
第9章 中心对称图形—平行四边形
9.4 矩形、菱形、正方形
八年级数学下册苏科版
第3课时 正方形
1
正方形的定义及性质
2
正方形的判定
CONTENTS
1
新知导入
填一填:
定义 边 角 对 角 线 对 称 性
平行 四边形
矩 形
菱 形
对边平行
且相等
对边平行 且相等
对边平行
四边都相等
对角相等
邻角互补
四个角
都是直角
对角相等
邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对
称图形
轴对称图形
中心对称图形
两组对边
分别平行
的四边形
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
轴对称图形
中心对称图形
CONTENTS
2
课程讲授
正方形的定义及性质
问题1.1 平行四边形经过怎样的变化就成为了正方形呢?
邻边相等
正方形
定 义:
有一组邻边相等并且的有一个角是直角的平行四边形是正方形.
平行四边形
有一个角是直角
正方形的定义及性质
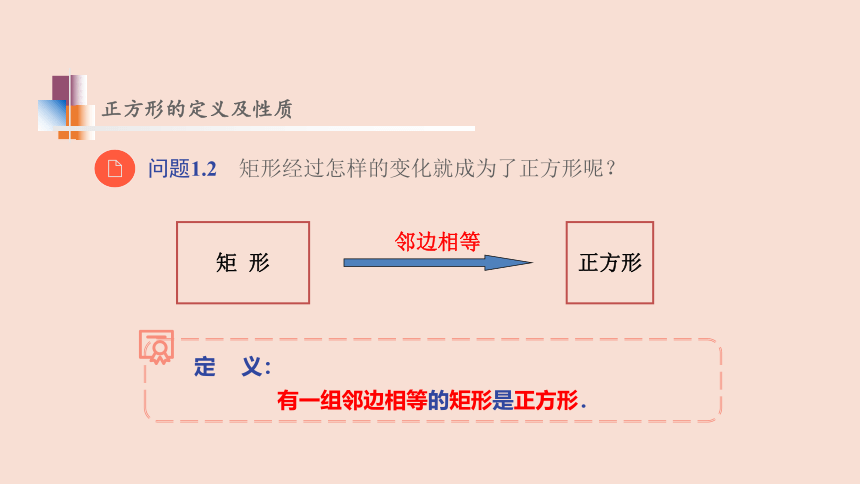
问题1.2 矩形经过怎样的变化就成为了正方形呢?
邻边相等
矩 形
正方形
定 义:
有一组邻边相等的矩形是正方形.
正方形的定义及性质
问题1.3 菱形经过怎样的变化就成为了正方形呢?
定 义:
有一个角是直角的菱形是正方形.
菱形
有一个角是直角
正方形
正方形的定义及性质
问题2 正方形是中心对称图形吗?是轴对称图形吗?如果是,有几条对称轴?
正方形既是中心对称图形,又是轴对称图形.它有四条对称轴(两条对角线,两组对边的中垂线)
正方形的定义及性质
问题3 正方形、菱形、矩形、平行四边形四者之间有什么关系?
矩形
菱形
正
方
形
平行四边形
正方形的定义及性质
问题4.1 正方形既能由矩形变换得到又能由菱形变换得到,那么正方形具有哪些性质?
猜想:正方形的四条边都相等,
四个角都是直角,
对角线相等且互相垂直平分.
正方形的定义及性质
问题4.2 已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°,AB=AC (正方形的定义).
又∵正方形是平行四边形,
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义),
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
正方形的定义及性质
问题4.3 已知:如图,正方形ABCD的对角线AC,BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
正方形的性质:
正方形的定义及性质
正方形的对边平行、四条边都相等.
边:
正方形的四个角都是直角.
角:
正方形的对角线对角线相等且互相垂直平分,
每条对角线平分一组对角.
对角线:
正方形的定义及性质
练一练:正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直
B.对角线互相平分
C.对角线相等
D.对角线平分一组对角
C
正方形的判定
问题5 前面我们学习了矩形和菱形,还记得它们的判定方法么?
①定义:有一个角是直角的平行四边形是矩形.
矩形的判别方法:
②对角线相等的平行四边形是矩形.
③三个角是直角的四边形是矩形.
菱形的判别方法:
①定义:有一组邻边相等的平行四边形是菱形.
②四条边相等的四边形是菱形.
③对角线互相垂直的平行四边形是菱形.
正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
正方形的判定
问题6.1 从对角线方面如何判定一个四边形是正方形呢?
猜想:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
正方形的判定
问题6.2 已知:如图,在矩形ABCD中,AC,BD是它的两条对角线且AC⊥DB. 求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
正方形的判定
问题6.3 已知:如图,在菱形ABCD中,AC,BD是它的两条对角线且AC=DB. 求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
正方形的判定
正方形的判定方法:
2.有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
1.有一组邻边相等且有一个角是直角的平行四边形是正方形.
正方形的判定
例 已知:如图,在正方形ABCD中,点A′、B′ 、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直
角,四条边相等).
∵ AA′=BB′=CC′=DD′ ,
∴D′A=A′B=B′C=C′D.
∴△AA′D′≌△ BB′A′≌△CC′B′≌△ DD′C′,
正方形的判定
∴∠2=∠3,
A′D′=B′A′=C′B′=D′C′.
∴四边形A′B′C′D′是菱形(四边相等的四边形是菱形).
∵ ∠A=90°,∴∠1+∠2=90°.
∵ ∠2=∠3,∴∠1+∠3=90°.
∴∠ D′A′B′= 90°.
∴菱形A′B′C′D′是正方形(有一个角是直角
的菱形是正方形).
正方形的判定
练一练:下列横线上填写正确的一项是( )
有一个角是直角的 是正方形;
有一组邻边相等的 是正方形.
A、矩形 菱形
B、菱形 平行四边形
C、平行四边形 矩形
D、菱形 矩形
D
CONTENTS
3
随堂练习
1.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
B
2.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
B
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件______________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
4.如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
证明:
(1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
CONTENTS
4
课堂小结
正 方 形
正方形的定义
正方形的判定
正方形的性质
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
1.对称性:菱形既是轴对称图形又是中心对称图形.
2.边:正方形的四条边相等.
3.角:正方形的四各角都是直角.
4.对角线:正方形的对角线相等且互相垂直平分.
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2.有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
第9章 中心对称图形—平行四边形
9.4 矩形、菱形、正方形
八年级数学下册苏科版
第3课时 正方形
1
正方形的定义及性质
2
正方形的判定
CONTENTS
1
新知导入
填一填:
定义 边 角 对 角 线 对 称 性
平行 四边形
矩 形
菱 形
对边平行
且相等
对边平行 且相等
对边平行
四边都相等
对角相等
邻角互补
四个角
都是直角
对角相等
邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对
称图形
轴对称图形
中心对称图形
两组对边
分别平行
的四边形
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
轴对称图形
中心对称图形
CONTENTS
2
课程讲授
正方形的定义及性质
问题1.1 平行四边形经过怎样的变化就成为了正方形呢?
邻边相等
正方形
定 义:
有一组邻边相等并且的有一个角是直角的平行四边形是正方形.
平行四边形
有一个角是直角
正方形的定义及性质
问题1.2 矩形经过怎样的变化就成为了正方形呢?
邻边相等
矩 形
正方形
定 义:
有一组邻边相等的矩形是正方形.
正方形的定义及性质
问题1.3 菱形经过怎样的变化就成为了正方形呢?
定 义:
有一个角是直角的菱形是正方形.
菱形
有一个角是直角
正方形
正方形的定义及性质
问题2 正方形是中心对称图形吗?是轴对称图形吗?如果是,有几条对称轴?
正方形既是中心对称图形,又是轴对称图形.它有四条对称轴(两条对角线,两组对边的中垂线)
正方形的定义及性质
问题3 正方形、菱形、矩形、平行四边形四者之间有什么关系?
矩形
菱形
正
方
形
平行四边形
正方形的定义及性质
问题4.1 正方形既能由矩形变换得到又能由菱形变换得到,那么正方形具有哪些性质?
猜想:正方形的四条边都相等,
四个角都是直角,
对角线相等且互相垂直平分.
正方形的定义及性质
问题4.2 已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°,AB=AC (正方形的定义).
又∵正方形是平行四边形,
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义),
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
正方形的定义及性质
问题4.3 已知:如图,正方形ABCD的对角线AC,BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
正方形的性质:
正方形的定义及性质
正方形的对边平行、四条边都相等.
边:
正方形的四个角都是直角.
角:
正方形的对角线对角线相等且互相垂直平分,
每条对角线平分一组对角.
对角线:
正方形的定义及性质
练一练:正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直
B.对角线互相平分
C.对角线相等
D.对角线平分一组对角
C
正方形的判定
问题5 前面我们学习了矩形和菱形,还记得它们的判定方法么?
①定义:有一个角是直角的平行四边形是矩形.
矩形的判别方法:
②对角线相等的平行四边形是矩形.
③三个角是直角的四边形是矩形.
菱形的判别方法:
①定义:有一组邻边相等的平行四边形是菱形.
②四条边相等的四边形是菱形.
③对角线互相垂直的平行四边形是菱形.
正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
正方形的判定
问题6.1 从对角线方面如何判定一个四边形是正方形呢?
猜想:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
正方形的判定
问题6.2 已知:如图,在矩形ABCD中,AC,BD是它的两条对角线且AC⊥DB. 求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
正方形的判定
问题6.3 已知:如图,在菱形ABCD中,AC,BD是它的两条对角线且AC=DB. 求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
正方形的判定
正方形的判定方法:
2.有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
1.有一组邻边相等且有一个角是直角的平行四边形是正方形.
正方形的判定
例 已知:如图,在正方形ABCD中,点A′、B′ 、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直
角,四条边相等).
∵ AA′=BB′=CC′=DD′ ,
∴D′A=A′B=B′C=C′D.
∴△AA′D′≌△ BB′A′≌△CC′B′≌△ DD′C′,
正方形的判定
∴∠2=∠3,
A′D′=B′A′=C′B′=D′C′.
∴四边形A′B′C′D′是菱形(四边相等的四边形是菱形).
∵ ∠A=90°,∴∠1+∠2=90°.
∵ ∠2=∠3,∴∠1+∠3=90°.
∴∠ D′A′B′= 90°.
∴菱形A′B′C′D′是正方形(有一个角是直角
的菱形是正方形).
正方形的判定
练一练:下列横线上填写正确的一项是( )
有一个角是直角的 是正方形;
有一组邻边相等的 是正方形.
A、矩形 菱形
B、菱形 平行四边形
C、平行四边形 矩形
D、菱形 矩形
D
CONTENTS
3
随堂练习
1.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
B
2.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
B
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件______________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
4.如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
证明:
(1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
CONTENTS
4
课堂小结
正 方 形
正方形的定义
正方形的判定
正方形的性质
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
1.对称性:菱形既是轴对称图形又是中心对称图形.
2.边:正方形的四条边相等.
3.角:正方形的四各角都是直角.
4.对角线:正方形的对角线相等且互相垂直平分.
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
2.有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
