2022_2023学年湘教版数学八年级上册2.5 全等三角形 第2课时 用“边角边”判定三角形全等 课件(共30张PPT)
文档属性
| 名称 | 2022_2023学年湘教版数学八年级上册2.5 全等三角形 第2课时 用“边角边”判定三角形全等 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 789.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 09:35:34 | ||
图片预览











文档简介
(共30张PPT)
第2章 三角形
2.5 全等三角形
第2课时 用“边角边”判定三角形全等
1.通过实际操作,体会满足“边角边”三角形的唯一性.
2.理解全等三角形的第一种判定方法“边角边”的正确性.
3.会用“边角边”判定两个三角形全等,初步用三角形全等解决简单几何问题.
◎重点:理解“边角边”能判定两个三角形全等.
◎难点:分析几何图形,寻找判定三角形全等的条件.
古希腊数学家欧几里得挑选了一些人们在长期实践中总结出来的公认的真命题作为证明的原始依据,称这些真命题为公理.我们把少数真命题作为基本事实.接下来,我们将要学习一些判定全等三角形的方法,这些都是基本事实.
全等三角形的判定方法1“边角边”
阅读课本本课时所有内容,解决下列问题.
1.(1)课堂操作:试在一张纸上用量角器和三角板画一个三角形,使得它的一个角为50°,夹这个角的两边分别为2 cm,2.5 cm,试比较你和其他同学画的三角形,大小与形状是否一样.(学法指导:先用量角器画一个角,再在角的两边截出线段的长)
相同.
(2)已知一个三角形的两边和夹角,画出的三角形是 唯一 确定的.
2.活动:将上面画出的三角形剪下,与同桌的三角形一起完成下面的操作.
(1)将两个三角形按课本“图2-38”所示摆放,试通过 平移 ,将它们完全重合;
唯一
平
移
(2)将两个三角形按课本“图2-39”所示摆放,试通过 旋转 ,将它们完全重合;
(3)将两个三角形按课本“图2-41”所示摆放,试通过 对折 ,将它们完全重合.
得出基本事实:两边和它们的夹角对应相等的两个三角形 全等 .简记为“边角边”或“SAS”(S表示边,A表示角).
旋转
对
折
全
等
3.注意:在用“边角边”判定方法中,包括“两边”“夹角”三个元素,其中两边是 夹这个角 的两边,角是这两边的所夹的角,不要误认为只要两个三角形中有两条边和一个角对应相等,这两个三角形就全等.
夹这个角
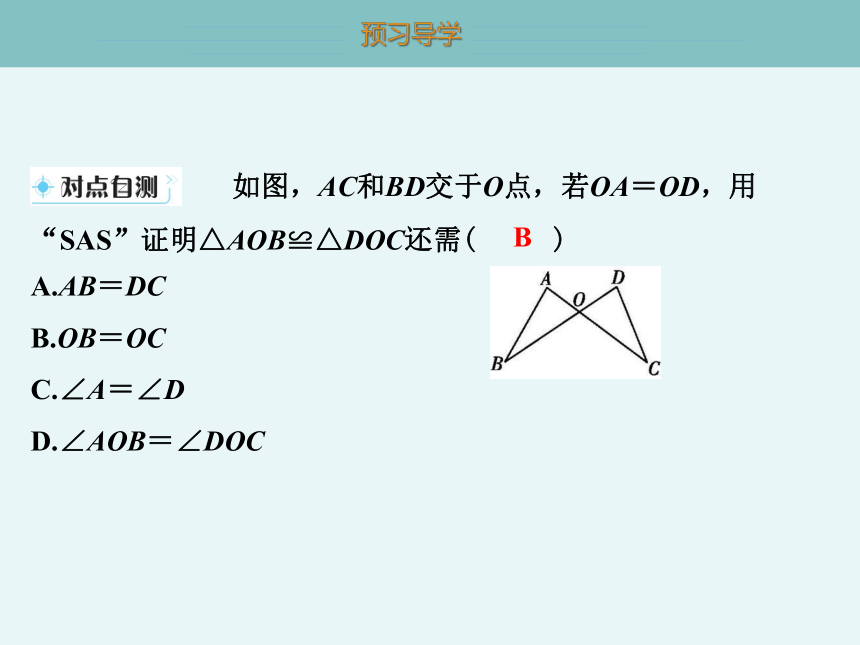
如图,AC和BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( B )
A.AB=DC
B.OB=OC
C.∠A=∠D
D.∠AOB=∠DOC
B
1.如图,在△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.
证明:∵AD平分∠BAC(已知),∴∠BAD=∠CAD(角平分线定义),
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),∴BD=CD(全等三角形对应边相等).
方法归纳交流 证明本题的思路是:
要证BD=CD △ABD≌△ACD
∠BAD=∠CAD.
一般的书写格式是①证所缺的条件;②列条件;③结论得证.
(学法指导:利用“SAS”来证明,隐含条件是AB=BA)2.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 ∠ABC=∠BAD (只填一个).
∠ABC=∠BAD
3.如图,△ABC和△ECD都是等边三角形(三条边都相等,每个角都等于60°的三角形),且点B,C,D在一条直线上.求证:BE=AD.
证明:由题意,AC=BC,∠ACD=∠BCE=120°,CD=CE,所以△ACD≌△BCE,所以AD=BE.
变式演练 任务驱动三中,把△CDE绕点C旋转一定角度,那么这时候BE和AD还相等吗?如果相等,给出证明;如果不相等,说明理由.
解:相等,证明如下:∵∠ACB=∠DCE=60°,
∴∠ACB+ ∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,又BC=AC, CE=CD,
∴△ACD≌△BCE(SAS),∴BE=AD.
解:相等,证明如下:∵∠ACB=∠DCE=60°,∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又BC=AC,CE=CD,∴△ACD≌△BCE(SAS),∴BE=AD.
方法归纳交流 证明两条直线平行,可利用全等三角形,证明这两条直线被第三条直线所截的 同位角相等 或 内错角相等 .
同位角相等
内错角相
等
4.如图,点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.求证:AB∥CD.
证明:∵AF=CE,∴AF+FE=CE+FE,即AE=CF,
又∵BE∥DF,∴∠AEB=∠CFD.
在△AEB和△CFD中,
∵
∴△AEB≌△CFD(SAS),
∴∠A=∠C,∴AB∥CD.
5.如图,AD∥BC,AD=CB,AE=CF.求证:AFD≌△CEB.
证明:∵AD∥BC(已知),
∴∠A=∠C(两直线平行,内错角相等),
又AE=CF,∴AE+EF=CF+EF(等式性质),即AF=CE,
在△AFD和△CEB中,,
∴△AFD≌△CEB(SAS).
方法归纳交流 1.根据边角边定理判定两个三角形全等,要找出两边及夹角对应相等的三个条件;2.找使结论成立所需条件,要充分利用已知条件(包括给出图形中的隐含条件,如公共边、公共角等),并要善于运用学过的定义、公理、定理.
1.如图,在△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
求证:△ABD≌△AEC.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠BAD=∠CAE.
在△ABD和△AEC中,
∴△ABD≌△AEC(SAS).
2.如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
解:(1)证明:∵点C是线段AB的中点,∴AC=BC,
又∵CD平分∠ACE,CE平分∠BCD,
∴∠1=∠2,∠2=∠3,∴∠1=∠3.
在△ACD和△BCE中,
∴△ACD≌△BCE.
(2)70°.
1下图所示的图形中是全等三角形的是 ( D )
D
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ
C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
2已知在△ADF和△BCE中,若AD=BC,∠A=∠B,直接能利用“SAS”证明△ADF≌△BCE的条件是 ( C )
A.AE=BF B.DF=CE
C.AF=BE D.∠CEB=∠DFA
3如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ △ACE ,理由是 SAS .
C
△ACE
SAS
4如图,有一块三角形镜子,小明不小心将其打碎为a,b两块,现需配一块同样形状、大小的镜子.为了方便起见,只需带上 a 块,其理由是 两边及其夹角对应相等的两个三角形全等 .
a
两边及其夹角对应相等的两个三角形全等
5如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是 ( B )
B
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
6如图,已知∠ACB=∠DBC,且在△ABC中,AB=3,AC=4,要证△ABC≌△DCB,则 ( A )
A.BD=4 B.BC=3
C.CD=3 D.AD=4
7如图,在△ABC中,AD⊥BC,D是BC的中点,则AC= 5 .
A
5
8如图,AB是∠DAC的平分线,AD=AC.
求证:BD=BC.
证明:∵AB是∠DAC的平分线,
∴∠DAB=∠CAB.
在△DAB与△CAB中,
∴△DAB≌△CAB,∴BD=BC.
9如图,OA=OB,OC=OD,∠AOB=∠COD,请说明AC=BD的理由.
解:理由如下:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
∵OA=OB,OC=OD,∴△OAC≌△OBD(SAS),
∴AC=BD.
10如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
证明:BC∥EF.理由如下:∵AE=DB,∴AE+BE=DB+BE,∴AB=DE.∵AC∥DF,∴∠A=∠D,∵AC=DF,
∴△ACB≌△DFE,∴∠FED=∠CBA,∴BC∥EF.
11如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF;(2)AB∥DE.
证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE,
在△ABC与△DEF中,∵BC=EF,∠ACB=∠DFE,AC=DF,
∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,∴∠ABC=∠DEF,∴AB∥DE.
第2章 三角形
2.5 全等三角形
第2课时 用“边角边”判定三角形全等
1.通过实际操作,体会满足“边角边”三角形的唯一性.
2.理解全等三角形的第一种判定方法“边角边”的正确性.
3.会用“边角边”判定两个三角形全等,初步用三角形全等解决简单几何问题.
◎重点:理解“边角边”能判定两个三角形全等.
◎难点:分析几何图形,寻找判定三角形全等的条件.
古希腊数学家欧几里得挑选了一些人们在长期实践中总结出来的公认的真命题作为证明的原始依据,称这些真命题为公理.我们把少数真命题作为基本事实.接下来,我们将要学习一些判定全等三角形的方法,这些都是基本事实.
全等三角形的判定方法1“边角边”
阅读课本本课时所有内容,解决下列问题.
1.(1)课堂操作:试在一张纸上用量角器和三角板画一个三角形,使得它的一个角为50°,夹这个角的两边分别为2 cm,2.5 cm,试比较你和其他同学画的三角形,大小与形状是否一样.(学法指导:先用量角器画一个角,再在角的两边截出线段的长)
相同.
(2)已知一个三角形的两边和夹角,画出的三角形是 唯一 确定的.
2.活动:将上面画出的三角形剪下,与同桌的三角形一起完成下面的操作.
(1)将两个三角形按课本“图2-38”所示摆放,试通过 平移 ,将它们完全重合;
唯一
平
移
(2)将两个三角形按课本“图2-39”所示摆放,试通过 旋转 ,将它们完全重合;
(3)将两个三角形按课本“图2-41”所示摆放,试通过 对折 ,将它们完全重合.
得出基本事实:两边和它们的夹角对应相等的两个三角形 全等 .简记为“边角边”或“SAS”(S表示边,A表示角).
旋转
对
折
全
等
3.注意:在用“边角边”判定方法中,包括“两边”“夹角”三个元素,其中两边是 夹这个角 的两边,角是这两边的所夹的角,不要误认为只要两个三角形中有两条边和一个角对应相等,这两个三角形就全等.
夹这个角
如图,AC和BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( B )
A.AB=DC
B.OB=OC
C.∠A=∠D
D.∠AOB=∠DOC
B
1.如图,在△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.
证明:∵AD平分∠BAC(已知),∴∠BAD=∠CAD(角平分线定义),
在△ABD与△ACD中,
∴△ABD≌△ACD(SAS),∴BD=CD(全等三角形对应边相等).
方法归纳交流 证明本题的思路是:
要证BD=CD △ABD≌△ACD
∠BAD=∠CAD.
一般的书写格式是①证所缺的条件;②列条件;③结论得证.
(学法指导:利用“SAS”来证明,隐含条件是AB=BA)2.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 ∠ABC=∠BAD (只填一个).
∠ABC=∠BAD
3.如图,△ABC和△ECD都是等边三角形(三条边都相等,每个角都等于60°的三角形),且点B,C,D在一条直线上.求证:BE=AD.
证明:由题意,AC=BC,∠ACD=∠BCE=120°,CD=CE,所以△ACD≌△BCE,所以AD=BE.
变式演练 任务驱动三中,把△CDE绕点C旋转一定角度,那么这时候BE和AD还相等吗?如果相等,给出证明;如果不相等,说明理由.
解:相等,证明如下:∵∠ACB=∠DCE=60°,
∴∠ACB+ ∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,又BC=AC, CE=CD,
∴△ACD≌△BCE(SAS),∴BE=AD.
解:相等,证明如下:∵∠ACB=∠DCE=60°,∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又BC=AC,CE=CD,∴△ACD≌△BCE(SAS),∴BE=AD.
方法归纳交流 证明两条直线平行,可利用全等三角形,证明这两条直线被第三条直线所截的 同位角相等 或 内错角相等 .
同位角相等
内错角相
等
4.如图,点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.求证:AB∥CD.
证明:∵AF=CE,∴AF+FE=CE+FE,即AE=CF,
又∵BE∥DF,∴∠AEB=∠CFD.
在△AEB和△CFD中,
∵
∴△AEB≌△CFD(SAS),
∴∠A=∠C,∴AB∥CD.
5.如图,AD∥BC,AD=CB,AE=CF.求证:AFD≌△CEB.
证明:∵AD∥BC(已知),
∴∠A=∠C(两直线平行,内错角相等),
又AE=CF,∴AE+EF=CF+EF(等式性质),即AF=CE,
在△AFD和△CEB中,,
∴△AFD≌△CEB(SAS).
方法归纳交流 1.根据边角边定理判定两个三角形全等,要找出两边及夹角对应相等的三个条件;2.找使结论成立所需条件,要充分利用已知条件(包括给出图形中的隐含条件,如公共边、公共角等),并要善于运用学过的定义、公理、定理.
1.如图,在△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
求证:△ABD≌△AEC.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠BAD=∠CAE.
在△ABD和△AEC中,
∴△ABD≌△AEC(SAS).
2.如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
解:(1)证明:∵点C是线段AB的中点,∴AC=BC,
又∵CD平分∠ACE,CE平分∠BCD,
∴∠1=∠2,∠2=∠3,∴∠1=∠3.
在△ACD和△BCE中,
∴△ACD≌△BCE.
(2)70°.
1下图所示的图形中是全等三角形的是 ( D )
D
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ
C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
2已知在△ADF和△BCE中,若AD=BC,∠A=∠B,直接能利用“SAS”证明△ADF≌△BCE的条件是 ( C )
A.AE=BF B.DF=CE
C.AF=BE D.∠CEB=∠DFA
3如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ △ACE ,理由是 SAS .
C
△ACE
SAS
4如图,有一块三角形镜子,小明不小心将其打碎为a,b两块,现需配一块同样形状、大小的镜子.为了方便起见,只需带上 a 块,其理由是 两边及其夹角对应相等的两个三角形全等 .
a
两边及其夹角对应相等的两个三角形全等
5如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是 ( B )
B
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
6如图,已知∠ACB=∠DBC,且在△ABC中,AB=3,AC=4,要证△ABC≌△DCB,则 ( A )
A.BD=4 B.BC=3
C.CD=3 D.AD=4
7如图,在△ABC中,AD⊥BC,D是BC的中点,则AC= 5 .
A
5
8如图,AB是∠DAC的平分线,AD=AC.
求证:BD=BC.
证明:∵AB是∠DAC的平分线,
∴∠DAB=∠CAB.
在△DAB与△CAB中,
∴△DAB≌△CAB,∴BD=BC.
9如图,OA=OB,OC=OD,∠AOB=∠COD,请说明AC=BD的理由.
解:理由如下:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
∵OA=OB,OC=OD,∴△OAC≌△OBD(SAS),
∴AC=BD.
10如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
证明:BC∥EF.理由如下:∵AE=DB,∴AE+BE=DB+BE,∴AB=DE.∵AC∥DF,∴∠A=∠D,∵AC=DF,
∴△ACB≌△DFE,∴∠FED=∠CBA,∴BC∥EF.
11如图,点B,C,E,F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.
求证:(1)△ABC≌△DEF;(2)AB∥DE.
证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE,
在△ABC与△DEF中,∵BC=EF,∠ACB=∠DFE,AC=DF,
∴△ABC≌△DEF(SAS).
(2)∵△ABC≌△DEF,∴∠ABC=∠DEF,∴AB∥DE.
同课章节目录
