镶嵌[下学期]
图片预览








文档简介
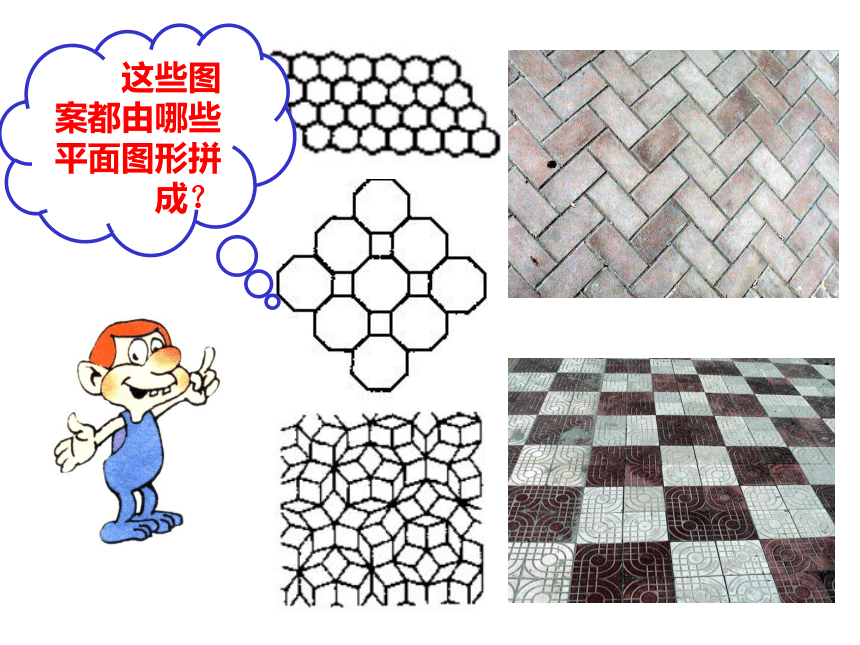
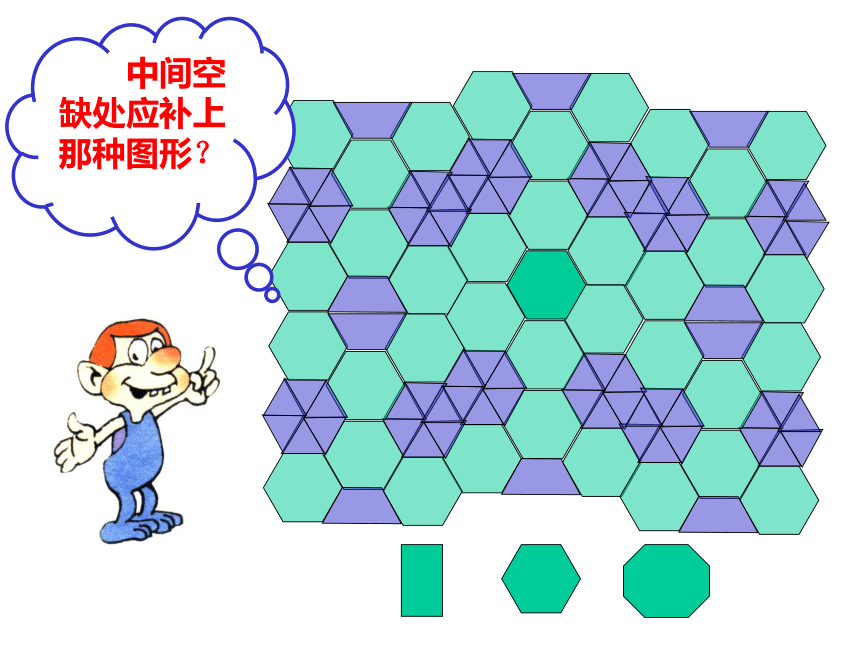
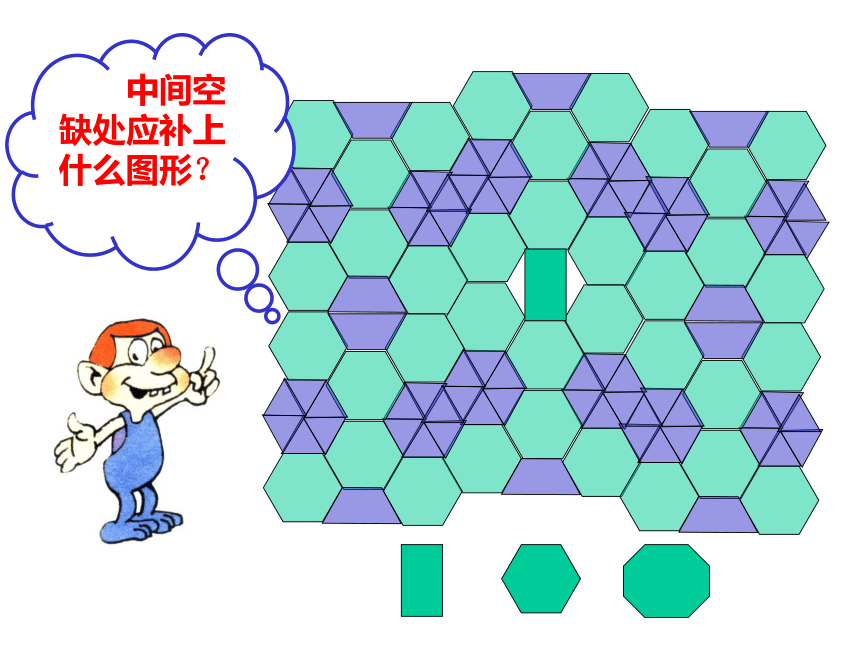
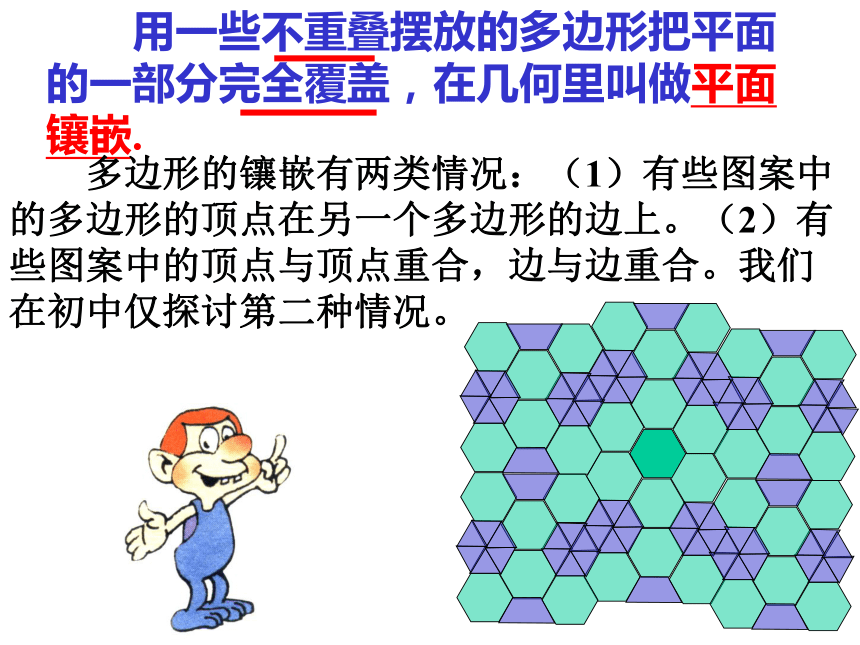
课件56张PPT。平面镶嵌数学中研究镶嵌的史料 据说,早在毕达哥拉斯时代,就已有人研究过多边形的镶嵌问题。而且,在著名的希尔伯特23个问题中,第18个就是用全等的多面体构造空间,是本节课所研究的问题的三维化。可见这个问题不仅源远流长,而且在现在也极有价值。 用一些不重叠摆放的多边形把平面的一部分完全覆盖,在几何里叫做平面镶嵌. 多边形的镶嵌有两类情况:(1)有些图案中的多边形的顶点在另一个多边形的边上。(2)有些图案中的顶点与顶点重合,边与边重合。我们在初中仅探讨第二种情况。请你欣赏下面请同学们做个实验:分别用正三角形,正方形,
正五边形,正六边形那些能镶嵌成一个平面图形?(1) 正三角形的平面镶嵌60°60°60°60°60°60°(2) 正方形的平面镶嵌90°(3) 正六边形的平面镶嵌120 °120 °120 °180o60o360o90o
540o108o720o120o能能能正三角形正方形正五边形正六边形643不能 你能只用一种正五边形拼成一个地面吗?为什么正五边形拼不成地面?而用正三角形可以?可以拼成一个地面条件是什么?7.4 平面镶嵌.swf因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。 仅用正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360°即:na=180°正三角形正方形想7.4 平面镶嵌.swf一
想正六边形正八边形用正三角形和正方形呢?2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数∴解为正三角形和正六边形拼拼看?m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有∵ m,n 为正整数∴解为用正四边形和正六边形呢?拼拼看?不能拼正方形和正八边形呢?2 m+3 n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有∵ m,n 为正整数∴解为正五边形和正十边形呢?设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解为 当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.即:ma+nB=360°规律: 当围绕一点拼在一起的几种正多边形的内角加在一起恰好组成一个周角时,这几种正多边形就能镶嵌.正十二边形与正方形、正六边形的平面镶嵌三种正多边形的平面镶嵌正三角形与正方形、正六边形的平面镶嵌思考同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?小红的妈妈准备把一些形状,大小相同的三角形花布丢掉
小红:妈妈,这些花布很好看,您为什么要丢掉呢?
妈妈:小红,这些布是很漂亮,可是面积太小,做不了什么东西只好丢掉!
小红:别扔,让我想想办法,把这些布头拼成一块漂亮的桌布吧。结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。发现二:
用一种形状、大小完全相同的三角形,四边形也能进行平面镶嵌发现一:
同一种正多边形进行平面镶嵌的图形只有三种:正三角形、正方形、正六边形多边形能进行平面镶嵌的条件是:(1)拼接在同一点的各个角的度数(2)相邻的多边形有公共边和是360度(2003年中考题)商店出售下列形状的地砖:①正方形;②长方形; ③正五边形;④正六边形。若只选择其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种边长为a的正方形与下列边长为a的正多边形组合起来,不能镶嵌成平面的是( )
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ② B. ② ③ C. ① ③ D. ① ④CB课堂练习:如图,足球由正五边形皮块(黑色)和正六边形皮块(白色)缝成。如果取下一黑两白两两相邻的三块皮块,能不能将这三块皮块连在一起铺平?为什么?答:正五边形的每个内角是540°/5=108 ° ,正六边形的每个内角是720 °/6=120 °
三块皮块有一个公共顶点。位于公共顶点处的三个内角分别是108 °,120 °,120 °,它们的和是348 °,小于360 °。所以不能将这三块皮块连在一起铺平。 练一练 1. 仅用正十边形能进行镶嵌吗? 为什么? 2. 只用一种正多边形能进行镶嵌的有
_____________________. 正三角形、正方形、 正六边形因为: na=360°
144n=360
n=2.5
所以:正十边形不能进行镶嵌1、下列多边形一定不能进行平面镶嵌的是( )
A、三角形 B、正方形 C、任意四边形 D、正八边形2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是( )
A、 3 B 、4 C、5 D 、63、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的边数为( )
A、3 B、4 C、5 D、6DBA布置作业A类:
请同学们充分发挥自己的创造力,设计两幅由多边形镶嵌而成的优美图案,并尝试写上一两句贴切的解说词。 B类:
(05陕西 )16.右图是用12个全等的等腰梯形镶嵌成的图形,这个图形中等腰梯形的上底长与下底长的比是__________。
(05山东)9.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是
(A)正方形 (B)正六边形
(C)正十二边形 (D)正十八边形
D1:2资料1:石子路镶嵌图案最多的图林
在北京故官御花园内,有许多颜色不同的细石子砌成的各种美丽图案的花石子路,据统计全园花石子路上的图案约有900幅,可以说是中国拥有石子路镶嵌图案最多的图林了。这些石子路图案的组成,是把全园作为一个整体来考虑设计的,因此显得极为统一协调。但是每幅图案又有它的独立的面貌,内容各异,图案的内容有人物、风景、花卉、博古等,种类繁多。其中的“颐和春色”、“关黄对刀”、“鹤鹿同春”等图案,造型优美,动态活泼、构图别致,色彩分明,沿路观赏,美不胜收。镶嵌画欣赏资料2:埃舍尔的作品——鸟分割的平面(2)引导欣赏挂图,感受镶嵌美资料3:镶嵌画材料来源十分丰富,有天然彩石、卵石、贝壳、螺钿、宝石、玉石和人造的玻璃料器、陶瓷、有机玻璃、金属和木料等。镶嵌方法有直接镶嵌法、预制法、反贴反上法、正贴正上法。除平面镶嵌外,也可以在浮雕上进行镶嵌,后者更能增强壁画的力度。
中国的镶嵌艺术具有悠久的历史和独特的风格。这些镶嵌艺术大多出现在工艺品上,如殷商时代的铜器曾有错金和错金嵌玉的装饰纹样出现。镶嵌画虽较少,仍可以从帝王御花园的甬道和民间的建筑中发现用卵石镶嵌地面和墙面的镶嵌装饰画面。当代中国艺术家也开始重视运用这种艺术形式,在一些重要建筑物的室内外创作了一些镶嵌画。资料3:用正多边形进行平面镶嵌只有以下这17组解有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。 虽然许多问题尚留待解决.不过有一件东西是肯定的,那就是美丽的数学镶嵌将会被不断地创造出来! 看你的了!
正五边形,正六边形那些能镶嵌成一个平面图形?(1) 正三角形的平面镶嵌60°60°60°60°60°60°(2) 正方形的平面镶嵌90°(3) 正六边形的平面镶嵌120 °120 °120 °180o60o360o90o
540o108o720o120o能能能正三角形正方形正五边形正六边形643不能 你能只用一种正五边形拼成一个地面吗?为什么正五边形拼不成地面?而用正三角形可以?可以拼成一个地面条件是什么?7.4 平面镶嵌.swf因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。 仅用正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360°即:na=180°正三角形正方形想7.4 平面镶嵌.swf一
想正六边形正八边形用正三角形和正方形呢?2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数∴解为正三角形和正六边形拼拼看?m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有∵ m,n 为正整数∴解为用正四边形和正六边形呢?拼拼看?不能拼正方形和正八边形呢?2 m+3 n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有∵ m,n 为正整数∴解为正五边形和正十边形呢?设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解为 当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.即:ma+nB=360°规律: 当围绕一点拼在一起的几种正多边形的内角加在一起恰好组成一个周角时,这几种正多边形就能镶嵌.正十二边形与正方形、正六边形的平面镶嵌三种正多边形的平面镶嵌正三角形与正方形、正六边形的平面镶嵌思考同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?小红的妈妈准备把一些形状,大小相同的三角形花布丢掉
小红:妈妈,这些花布很好看,您为什么要丢掉呢?
妈妈:小红,这些布是很漂亮,可是面积太小,做不了什么东西只好丢掉!
小红:别扔,让我想想办法,把这些布头拼成一块漂亮的桌布吧。结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。发现二:
用一种形状、大小完全相同的三角形,四边形也能进行平面镶嵌发现一:
同一种正多边形进行平面镶嵌的图形只有三种:正三角形、正方形、正六边形多边形能进行平面镶嵌的条件是:(1)拼接在同一点的各个角的度数(2)相邻的多边形有公共边和是360度(2003年中考题)商店出售下列形状的地砖:①正方形;②长方形; ③正五边形;④正六边形。若只选择其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种边长为a的正方形与下列边长为a的正多边形组合起来,不能镶嵌成平面的是( )
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ② B. ② ③ C. ① ③ D. ① ④CB课堂练习:如图,足球由正五边形皮块(黑色)和正六边形皮块(白色)缝成。如果取下一黑两白两两相邻的三块皮块,能不能将这三块皮块连在一起铺平?为什么?答:正五边形的每个内角是540°/5=108 ° ,正六边形的每个内角是720 °/6=120 °
三块皮块有一个公共顶点。位于公共顶点处的三个内角分别是108 °,120 °,120 °,它们的和是348 °,小于360 °。所以不能将这三块皮块连在一起铺平。 练一练 1. 仅用正十边形能进行镶嵌吗? 为什么? 2. 只用一种正多边形能进行镶嵌的有
_____________________. 正三角形、正方形、 正六边形因为: na=360°
144n=360
n=2.5
所以:正十边形不能进行镶嵌1、下列多边形一定不能进行平面镶嵌的是( )
A、三角形 B、正方形 C、任意四边形 D、正八边形2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是( )
A、 3 B 、4 C、5 D 、63、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形的每一个顶点周围都有6个正多边形,则该正多边形的边数为( )
A、3 B、4 C、5 D、6DBA布置作业A类:
请同学们充分发挥自己的创造力,设计两幅由多边形镶嵌而成的优美图案,并尝试写上一两句贴切的解说词。 B类:
(05陕西 )16.右图是用12个全等的等腰梯形镶嵌成的图形,这个图形中等腰梯形的上底长与下底长的比是__________。
(05山东)9.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是
(A)正方形 (B)正六边形
(C)正十二边形 (D)正十八边形
D1:2资料1:石子路镶嵌图案最多的图林
在北京故官御花园内,有许多颜色不同的细石子砌成的各种美丽图案的花石子路,据统计全园花石子路上的图案约有900幅,可以说是中国拥有石子路镶嵌图案最多的图林了。这些石子路图案的组成,是把全园作为一个整体来考虑设计的,因此显得极为统一协调。但是每幅图案又有它的独立的面貌,内容各异,图案的内容有人物、风景、花卉、博古等,种类繁多。其中的“颐和春色”、“关黄对刀”、“鹤鹿同春”等图案,造型优美,动态活泼、构图别致,色彩分明,沿路观赏,美不胜收。镶嵌画欣赏资料2:埃舍尔的作品——鸟分割的平面(2)引导欣赏挂图,感受镶嵌美资料3:镶嵌画材料来源十分丰富,有天然彩石、卵石、贝壳、螺钿、宝石、玉石和人造的玻璃料器、陶瓷、有机玻璃、金属和木料等。镶嵌方法有直接镶嵌法、预制法、反贴反上法、正贴正上法。除平面镶嵌外,也可以在浮雕上进行镶嵌,后者更能增强壁画的力度。
中国的镶嵌艺术具有悠久的历史和独特的风格。这些镶嵌艺术大多出现在工艺品上,如殷商时代的铜器曾有错金和错金嵌玉的装饰纹样出现。镶嵌画虽较少,仍可以从帝王御花园的甬道和民间的建筑中发现用卵石镶嵌地面和墙面的镶嵌装饰画面。当代中国艺术家也开始重视运用这种艺术形式,在一些重要建筑物的室内外创作了一些镶嵌画。资料3:用正多边形进行平面镶嵌只有以下这17组解有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。 虽然许多问题尚留待解决.不过有一件东西是肯定的,那就是美丽的数学镶嵌将会被不断地创造出来! 看你的了!
