数学人教A版(2019)选择性必修第一册2.4.2圆的一般方程 教案(表格式)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.4.2圆的一般方程 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 21:16:57 | ||
图片预览



文档简介
课程基本信息
课题 2.4.2圆的一般方程
教科书 书名:《数学》选择性必修第一册 出版社: 人民教育出版社 出版日期:2020年5月
教学目标
教学目标:(1)掌握圆的一般方程,会用一般方程求圆心半径等。 (2)会用待定系数法、几何法求圆的一般方程 (3)体会数学形结合的数学思想方法。 教学重点:求圆的一般方程,求与圆有关的轨迹方程。 教学难点:运用一般方程解决相关问题。
教学过程
时间 教学环节 主要师生活动
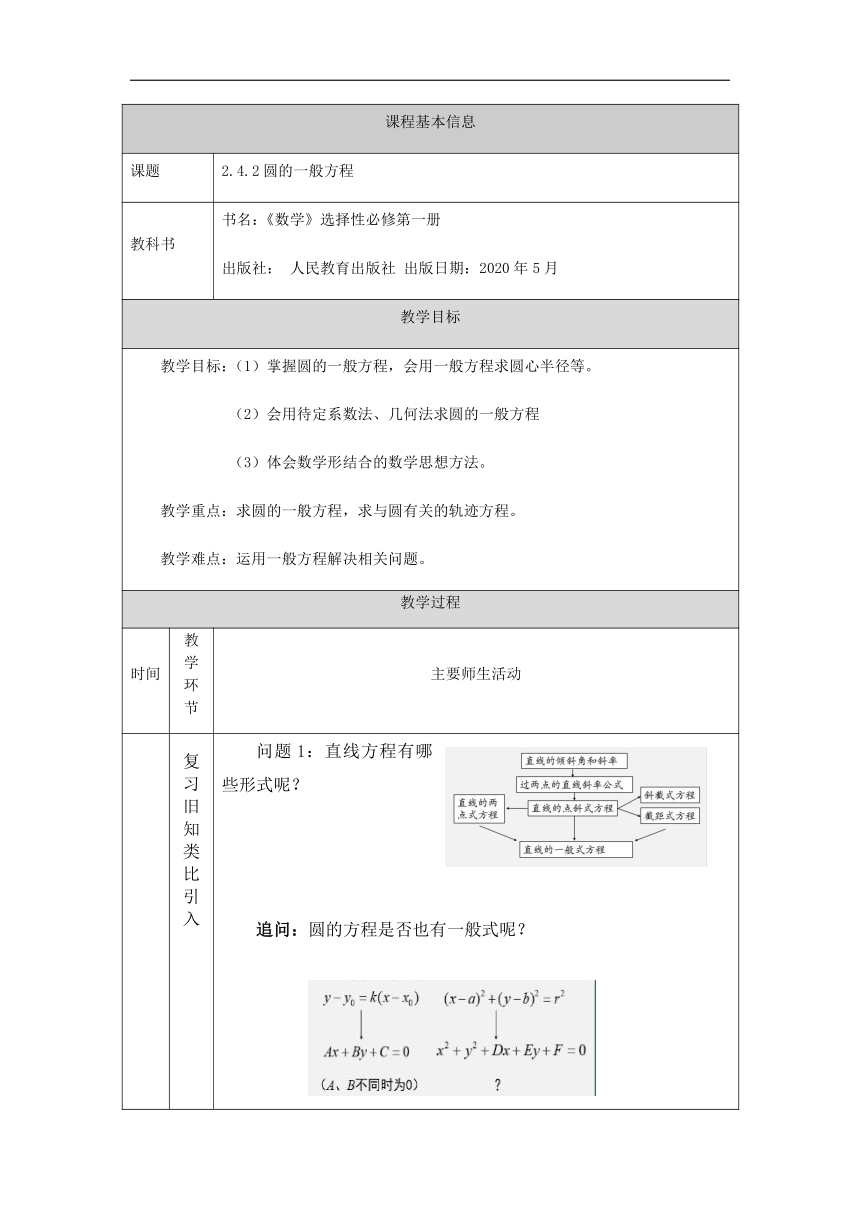
复习旧知类比引入 确立对象建立方程 对比方程观察特征 例题讲解强化新知 解题小结方法提升 应用方程知识升华 课堂小结布置作业 问题1:直线方程有哪些形式呢? 追问:圆的方程是否也有一般式呢? 问题2: 方程是否表示圆呢? 尝试讨论下面问题: (1)这类方程是否一定都是圆的方程? (2)如果这类方程表示一个圆,其系数应具有怎样的条件? (3)这类方程是圆的方程时,能否直接根据系数写出此圆的圆心坐标,求出圆的半径? (4)这类方程如果不表示一个圆,方程会表示什么曲线? 由于标准方程中,等式右方为半径的平方>0,因此我们需要得到一个D、E、F同时满足的不等关系。 通过配方把x2+y2+Dx+Ey+F=0化成 提到一个方程x2+y2+Dx+Ey+F=0是圆的一般方程,这是有前提的,首先需要在方程确实表示一个圆的情况下称圆的方程,而条件D2+E2-4F>0是充要条件.第(2)种情况,D2+E2-4F=0,此时方程x2+y2+Dx+Ey+F=0表示一个点,这个点可以看成是半径等于0的“圆”.第(3)种情形,D2+E2-4F<0,方程并不表示任何图形. 当D2+E2-4F<0时,我们把x2+y2+Dx+Ey+F=0称为圆的一般方程。 问题3:圆的标准方程与圆的一般方程各有什么特点呢? 例1 判断下列方程表示什么图形,并说明理由. (1) (2) 根据前面的学习,可以有两种方式。方法1,进行配方变形,找圆心求半径;方法2,利用刚刚学过的公式来求。两种方法从本质上来说是一致的,都体现了曲线与方程的概念。 题1变形后,可直接得到圆为(1,-2),半径 ;而题2中含有参数,所以变形后,要对等式右方进行讨论,当,只表示点(0,0),当 时才能表示圆。参数范围的产生,主要由于半径为正数造成的。相比而言,利用关于D、E、F的关系式不如配方转化成标准方程更直观、更方便。 例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求这个圆的圆心坐标和半径. 解:设圆的方程是 x2+y2+Dx+Ey+F=0. ① 因为O,M1,M2三点都在圆上,所以它们的坐标都是方程①的解.把它们的坐标依次代入方程①,得到关于D,E,F的一个三元一次方程组 解这个方程组,得 所以,所求圆的方程是x2+y2-8x+6y=0. 由前面的讨论可知,所求圆的圆心坐标是(4,-3),半径. 问题4:什么是待定系数法?如何运用待定系数法求圆的方程呢? 待定系数法,一般先写出含有未知系数的解的形式(如一种类型的方程、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法. 用待定系数法求圆的方程需要这三步。 (1)根据题意,选择标准方程或一般方程; (2)根据条件列出关于a,b,r或D,E,F的方程组; (3)解出参数,得到标准方程或一般方程. 当判定四点共圆时,先通过三点确定一个圆,本题中先通过求出圆的方程(为直径),然后代入满足,四个点都在x2+y2-8x+6y=0上. 例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程. 问题5:同学们如何理解轨迹和轨迹方程呢? 轨迹,顾名思义就是动点按一定轨道运动所留下的痕迹。它是一种点的集合,是一类曲线,而轨迹方程则是曲线的代数表示. 本题中,欲求M的轨迹方程,只要通过已知条件,求出M的坐标所满足的代数关系即可。显然,M点的生成原因是解题的关键.在已知中有两个定量,点B坐标和动点A坐标所满足的方程. 解:设点M的坐标是(x,y),点A的坐标是(x0,y0).由于点B的坐标是(4,3),且M是线段AB的中点,所以 , , 于是有 ① 因为点A在圆(x+1)2+y2=4上运动,所以点A的坐标满足圆的方程,即(x0+1)2+y20=4. ② 把①代入②,得(2x-4+1)2+(2y-3)2=4,整理,得 . 变形 若以OA、OB为边作平行四边形OAPB,求P轨迹方程. 注意共线情形,要求. 问题6:这节课学习了哪些知识?运用了哪些思路与方法呢? 课后作业(见学生资源)
课题 2.4.2圆的一般方程
教科书 书名:《数学》选择性必修第一册 出版社: 人民教育出版社 出版日期:2020年5月
教学目标
教学目标:(1)掌握圆的一般方程,会用一般方程求圆心半径等。 (2)会用待定系数法、几何法求圆的一般方程 (3)体会数学形结合的数学思想方法。 教学重点:求圆的一般方程,求与圆有关的轨迹方程。 教学难点:运用一般方程解决相关问题。
教学过程
时间 教学环节 主要师生活动
复习旧知类比引入 确立对象建立方程 对比方程观察特征 例题讲解强化新知 解题小结方法提升 应用方程知识升华 课堂小结布置作业 问题1:直线方程有哪些形式呢? 追问:圆的方程是否也有一般式呢? 问题2: 方程是否表示圆呢? 尝试讨论下面问题: (1)这类方程是否一定都是圆的方程? (2)如果这类方程表示一个圆,其系数应具有怎样的条件? (3)这类方程是圆的方程时,能否直接根据系数写出此圆的圆心坐标,求出圆的半径? (4)这类方程如果不表示一个圆,方程会表示什么曲线? 由于标准方程中,等式右方为半径的平方>0,因此我们需要得到一个D、E、F同时满足的不等关系。 通过配方把x2+y2+Dx+Ey+F=0化成 提到一个方程x2+y2+Dx+Ey+F=0是圆的一般方程,这是有前提的,首先需要在方程确实表示一个圆的情况下称圆的方程,而条件D2+E2-4F>0是充要条件.第(2)种情况,D2+E2-4F=0,此时方程x2+y2+Dx+Ey+F=0表示一个点,这个点可以看成是半径等于0的“圆”.第(3)种情形,D2+E2-4F<0,方程并不表示任何图形. 当D2+E2-4F<0时,我们把x2+y2+Dx+Ey+F=0称为圆的一般方程。 问题3:圆的标准方程与圆的一般方程各有什么特点呢? 例1 判断下列方程表示什么图形,并说明理由. (1) (2) 根据前面的学习,可以有两种方式。方法1,进行配方变形,找圆心求半径;方法2,利用刚刚学过的公式来求。两种方法从本质上来说是一致的,都体现了曲线与方程的概念。 题1变形后,可直接得到圆为(1,-2),半径 ;而题2中含有参数,所以变形后,要对等式右方进行讨论,当,只表示点(0,0),当 时才能表示圆。参数范围的产生,主要由于半径为正数造成的。相比而言,利用关于D、E、F的关系式不如配方转化成标准方程更直观、更方便。 例2 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求这个圆的圆心坐标和半径. 解:设圆的方程是 x2+y2+Dx+Ey+F=0. ① 因为O,M1,M2三点都在圆上,所以它们的坐标都是方程①的解.把它们的坐标依次代入方程①,得到关于D,E,F的一个三元一次方程组 解这个方程组,得 所以,所求圆的方程是x2+y2-8x+6y=0. 由前面的讨论可知,所求圆的圆心坐标是(4,-3),半径. 问题4:什么是待定系数法?如何运用待定系数法求圆的方程呢? 待定系数法,一般先写出含有未知系数的解的形式(如一种类型的方程、算式或表达式),然后再根据问题所给的条件解得所设的未知系数.由于其中的系数是未知和待定的,这类方法就被称为待定系数法. 用待定系数法求圆的方程需要这三步。 (1)根据题意,选择标准方程或一般方程; (2)根据条件列出关于a,b,r或D,E,F的方程组; (3)解出参数,得到标准方程或一般方程. 当判定四点共圆时,先通过三点确定一个圆,本题中先通过求出圆的方程(为直径),然后代入满足,四个点都在x2+y2-8x+6y=0上. 例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程. 问题5:同学们如何理解轨迹和轨迹方程呢? 轨迹,顾名思义就是动点按一定轨道运动所留下的痕迹。它是一种点的集合,是一类曲线,而轨迹方程则是曲线的代数表示. 本题中,欲求M的轨迹方程,只要通过已知条件,求出M的坐标所满足的代数关系即可。显然,M点的生成原因是解题的关键.在已知中有两个定量,点B坐标和动点A坐标所满足的方程. 解:设点M的坐标是(x,y),点A的坐标是(x0,y0).由于点B的坐标是(4,3),且M是线段AB的中点,所以 , , 于是有 ① 因为点A在圆(x+1)2+y2=4上运动,所以点A的坐标满足圆的方程,即(x0+1)2+y20=4. ② 把①代入②,得(2x-4+1)2+(2y-3)2=4,整理,得 . 变形 若以OA、OB为边作平行四边形OAPB,求P轨迹方程. 注意共线情形,要求. 问题6:这节课学习了哪些知识?运用了哪些思路与方法呢? 课后作业(见学生资源)
