7.4课题学习 镶嵌[下学期]
文档属性
| 名称 | 7.4课题学习 镶嵌[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-23 22:50:00 | ||
图片预览








文档简介
课件50张PPT。7.4课题学习 镶嵌铺地板的学问有些地板的拼合图案如图所示,它是用正方形的地砖铺成的,为什么用这样形状的地砖能铺成无缝隙的地板呢?
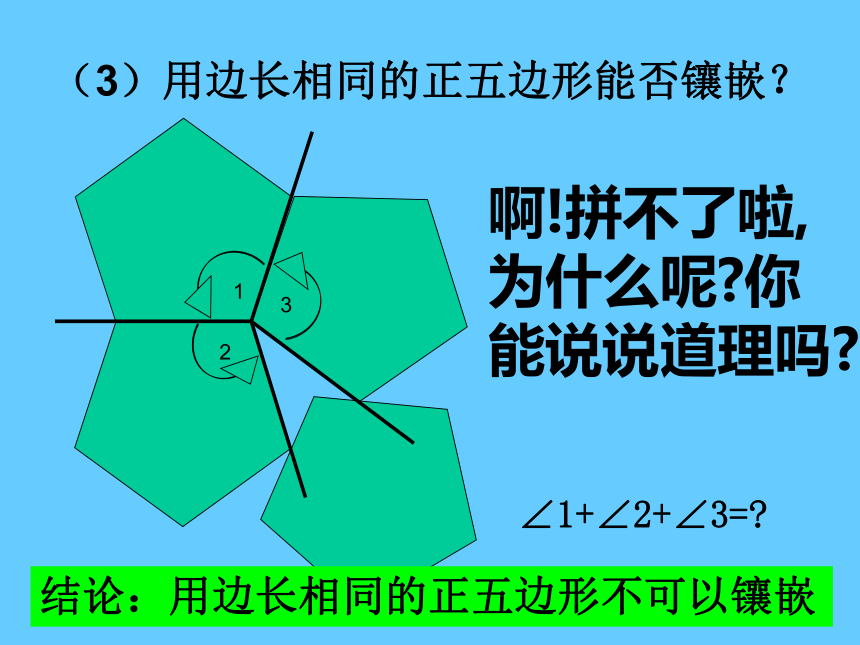
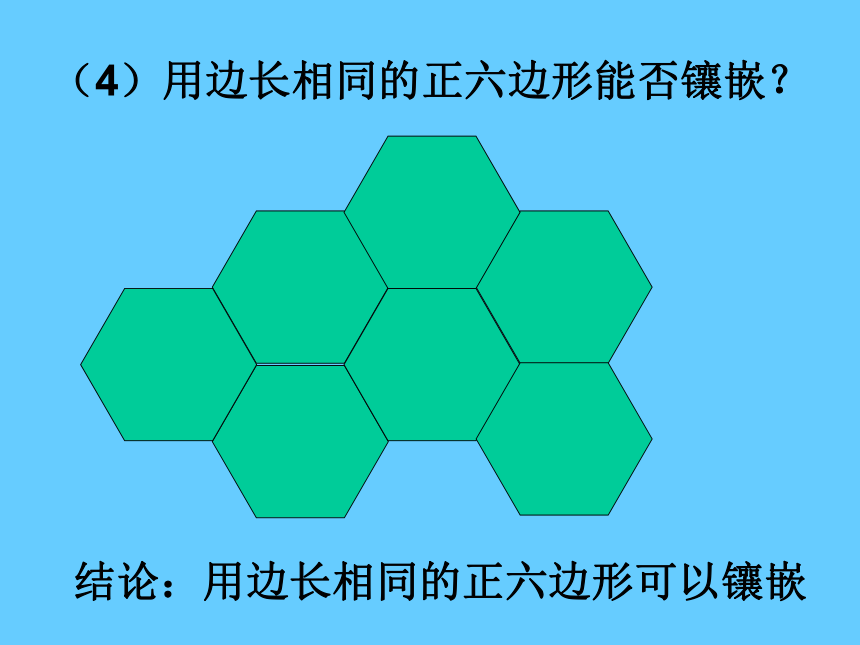
看一看 从数学角度看,用一些不重叠摆放的图形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题注意:各种图形拼接后要既无缝隙,又不重叠壁纸请你欣赏壁砖美丽的图案请你欣赏地砖请你欣赏美丽的图案请你欣赏图案欣赏做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(3)用边长相同的正五边形能否镶嵌?结论:用边长相同的正五边形不可以镶嵌(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?如图,为什么有的多边形可以拼凑成一个平面图形,而有的却又不可以呢?正三角形镶嵌正六边形镶嵌正五边形正八边形想一想能镶嵌能镶嵌不能镶嵌不能镶嵌能镶嵌K= 6K= 4K= 3K= 4K= 360°90°108°108°120°n =3n =6n =4n =5能镶嵌不能镶嵌不能镶嵌能镶嵌6×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°能镶嵌得出结论: 如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)! 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。
哪些正多边形单独能镶嵌?为什么?
正七边形、正八边形、正九边形、正十边形、正十二边形能吗?为什么?正三角形正方形正六边形知识概括正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度”如下正多边形中,哪些可单独镶嵌?知识概括 要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360° 在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°, 这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°所以说:在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可镶嵌.知识概括3×60°+ 2 ×90°= 360° 3×60+2 ×90°=360°4×60+1 ×120°=360°正三角形正四边形正三角形正六角形探究活动:用两种正多边形,哪两种正多边形能够进行镶嵌?得出结论:用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
(两种正多边形的边长相等)
做一做正三角形与正方形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?正三角形与正六边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做正四边形与正六边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做正五边形与正十边形正三角形与正十二边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做做一做(一) 用形状、大小完全相同的三角形能否密铺?结论:
任意形状、大小完全相同的三角形能密铺 ,在每个拼接点处有六个角,而这六个角的和恰好是这个三角形的内角和的两倍,也就是它们的和为360o,且相等的边互相重合结论:
任意形状、大小相同的四边形能密铺 ,在每个拼接点处有四个角,而这四个角的和恰好是这个四边形的内角和,也就是它们的和为360o,且相等的边互相重合做一做(二)用同一种四边形能否密铺?正三角形、正方形与正六边形了解正方形、正六边形与正十二边形了解这节课你有哪些收获? 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。正三角形与正方形正三角形正方形正六边形正三角形与正六边形正三角形与正十二边形如:收获与启示 用一种正多边形镶嵌的规律:正多边形的内角是360°的约数(或360°是这个正多边形的整数倍)!
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)
数学试验对学习的帮组和启发镶嵌演示镶嵌演示镶嵌演示镶嵌演示镶嵌演示镶嵌演示112233433请你欣赏请你欣赏请你欣赏请你欣赏同学们,再见
看一看 从数学角度看,用一些不重叠摆放的图形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题注意:各种图形拼接后要既无缝隙,又不重叠壁纸请你欣赏壁砖美丽的图案请你欣赏地砖请你欣赏美丽的图案请你欣赏图案欣赏做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(3)用边长相同的正五边形能否镶嵌?结论:用边长相同的正五边形不可以镶嵌(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?如图,为什么有的多边形可以拼凑成一个平面图形,而有的却又不可以呢?正三角形镶嵌正六边形镶嵌正五边形正八边形想一想能镶嵌能镶嵌不能镶嵌不能镶嵌能镶嵌K= 6K= 4K= 3K= 4K= 360°90°108°108°120°n =3n =6n =4n =5能镶嵌不能镶嵌不能镶嵌能镶嵌6×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°能镶嵌得出结论: 如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)! 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。
哪些正多边形单独能镶嵌?为什么?
正七边形、正八边形、正九边形、正十边形、正十二边形能吗?为什么?正三角形正方形正六边形知识概括正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度”如下正多边形中,哪些可单独镶嵌?知识概括 要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360° 在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°, 这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°所以说:在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可镶嵌.知识概括3×60°+ 2 ×90°= 360° 3×60+2 ×90°=360°4×60+1 ×120°=360°正三角形正四边形正三角形正六角形探究活动:用两种正多边形,哪两种正多边形能够进行镶嵌?得出结论:用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
(两种正多边形的边长相等)
做一做正三角形与正方形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?正三角形与正六边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做正四边形与正六边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做正五边形与正十边形正三角形与正十二边形下列不同正多边形能否镶嵌?
正三角形与正方形?
正三角形与正六边形?
正四边形与正六边形?
正五边形与正十边形?
正三角形与正十二边形?做一做做一做(一) 用形状、大小完全相同的三角形能否密铺?结论:
任意形状、大小完全相同的三角形能密铺 ,在每个拼接点处有六个角,而这六个角的和恰好是这个三角形的内角和的两倍,也就是它们的和为360o,且相等的边互相重合结论:
任意形状、大小相同的四边形能密铺 ,在每个拼接点处有四个角,而这四个角的和恰好是这个四边形的内角和,也就是它们的和为360o,且相等的边互相重合做一做(二)用同一种四边形能否密铺?正三角形、正方形与正六边形了解正方形、正六边形与正十二边形了解这节课你有哪些收获? 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。正三角形与正方形正三角形正方形正六边形正三角形与正六边形正三角形与正十二边形如:收获与启示 用一种正多边形镶嵌的规律:正多边形的内角是360°的约数(或360°是这个正多边形的整数倍)!
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)
数学试验对学习的帮组和启发镶嵌演示镶嵌演示镶嵌演示镶嵌演示镶嵌演示镶嵌演示112233433请你欣赏请你欣赏请你欣赏请你欣赏同学们,再见
