2022-2023学年人教版八年级数学上册15.1.1 从分数到分式 课件 (共17张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册15.1.1 从分数到分式 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1. 整数2除以整数3能整除吗?那它的结果是多少?
回顾旧知
分数
分式
2. 整式a除以整式(a+1)能整除吗?那它的结果该如何表示?
类比
整数
整数
整式
整式
不能整除
不能整除
类比
第十五章 分 式
15.1.1 从分数到分式
理解并掌握分式的定义
理解分式有意义的条件以及值为零的条件
经历类比分数以及整式的过程,体会转化思想、类比思想、由特殊到一般的思想。
学习目标
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
长方形的面积为S,长为7,宽应为______.
长方形的面积为S,长为a,宽应为______.
S
a
导入新课
情境引入
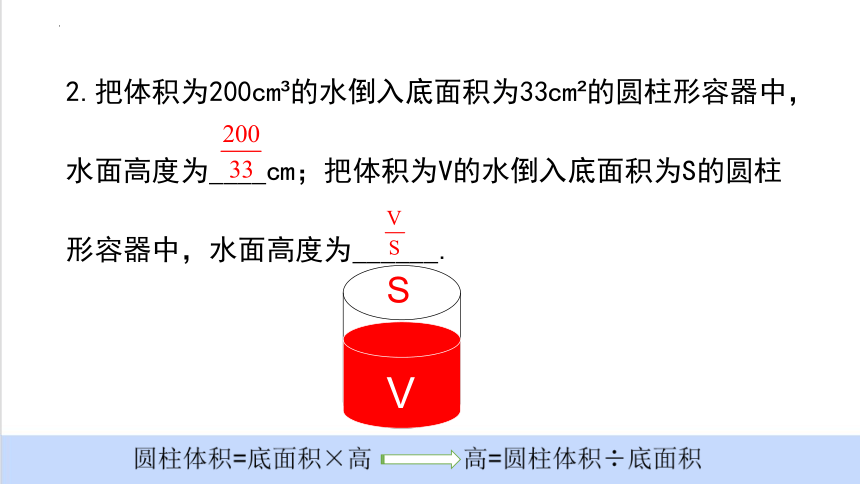
2.把体积为200cm 的水倒入底面积为33cm 的圆柱形容器中,水面高度为____cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为______.
V
S
3.一艘轮船在静水中的最大航速为30km/h,江水的流速为 v km/h,它以最大航速沿江顺流航行行驶速度 km,以最大航速逆流航行行驶速度 km,
则轮船顺流航行90km所用时间为 h.
逆流航行60km所用时间为 h.
讲授新课
分式的概念
问题1:请将上面问题中得到的式子分分类:
单项式:
多项式:
既不是单项式也不是多项式:
整
式
一
问题2 :式子
它们有什么相同点和不同点?
相同点
不同点
(观察分母)
从形式上都具有分数 形式
分母中是否含有字母
A
B
分子A、分母B都是整式
整式
新式子
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B为分式的分母.
分式的定义
分数
类比分数、分式的概念及表达形式:
类比
s
÷
(S+1)
=
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式=商式
如:
整数
整数
分数
整式(A)
整式(B)
分式( )
A
B
s
(S+1)
既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数、式通性
整数
分数
有理数
数的扩充
整式
分式
有理式
式的扩充
小试牛刀
1.从下列各式中选出分式所对应的选项。
整式
整式
分式
整式
分式
整式
分式
分式
分式
整式
一组:A B C D E
二组:A B C D E
式子中含有多项时,若其中有一项分母含有字母,则该式也为分式
不用化简只看形式
分式有意义的条件
二
问题3.已知分式 请你计算分式的值。
对于分式
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
分式有意义的条件
······ 3 2 1 ······
······ ······
0
0
-1
无意义
例1:下列分式中的字母满足什么条件时分式有意义?
(2)当x 时,分式 有意义;
x≠y
(1)当a 时,分式 有意义;
(3)当m 时,分式 有意义;
(4)当 时,分式 有意义.
做一做:
(5)当b 时,分式 有意义.
(6)当x 时,分式 有意义.
(2)当x 时,分式 有意义;
为任意实数
拓展练习:
(1)当x 时,分式 有意义;
变式训练
(1)当 时,分式 的值为零.
想一想:分式 的值为零应满足什么条件?
当A=0而 B≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
分式值为零的条件
三
x=2
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴ 解得x=2.
三二
随堂练习
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
2.当a=-1时,分式 的值( )
A.没有意义 B.等于零 C.等于1 D.等于-1
A
3.当x为任意实数时,下列分式一定有意义的是( )
A.
B.
C.
D.
B
课堂小结
分式
定义
值为零的条件
有意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子 叫做分式 ,其中,A叫做分式的分子,B叫做分式的分母.
分式 有意义的条件是B ≠0.
分式 值为零的条件是A=0且B ≠0.
1. 整数2除以整数3能整除吗?那它的结果是多少?
回顾旧知
分数
分式
2. 整式a除以整式(a+1)能整除吗?那它的结果该如何表示?
类比
整数
整数
整式
整式
不能整除
不能整除
类比
第十五章 分 式
15.1.1 从分数到分式
理解并掌握分式的定义
理解分式有意义的条件以及值为零的条件
经历类比分数以及整式的过程,体会转化思想、类比思想、由特殊到一般的思想。
学习目标
1.长方形的面积为10cm ,长为7cm,宽应为____cm;
长方形的面积为S,长为7,宽应为______.
长方形的面积为S,长为a,宽应为______.
S
a
导入新课
情境引入
2.把体积为200cm 的水倒入底面积为33cm 的圆柱形容器中,水面高度为____cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为______.
V
S
3.一艘轮船在静水中的最大航速为30km/h,江水的流速为 v km/h,它以最大航速沿江顺流航行行驶速度 km,以最大航速逆流航行行驶速度 km,
则轮船顺流航行90km所用时间为 h.
逆流航行60km所用时间为 h.
讲授新课
分式的概念
问题1:请将上面问题中得到的式子分分类:
单项式:
多项式:
既不是单项式也不是多项式:
整
式
一
问题2 :式子
它们有什么相同点和不同点?
相同点
不同点
(观察分母)
从形式上都具有分数 形式
分母中是否含有字母
A
B
分子A、分母B都是整式
整式
新式子
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B为分式的分母.
分式的定义
分数
类比分数、分式的概念及表达形式:
类比
s
÷
(S+1)
=
3 ÷ 5 =
被除数÷除数=商数
如:
被除式÷除式=商式
如:
整数
整数
分数
整式(A)
整式(B)
分式( )
A
B
s
(S+1)
既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数、式通性
整数
分数
有理数
数的扩充
整式
分式
有理式
式的扩充
小试牛刀
1.从下列各式中选出分式所对应的选项。
整式
整式
分式
整式
分式
整式
分式
分式
分式
整式
一组:A B C D E
二组:A B C D E
式子中含有多项时,若其中有一项分母含有字母,则该式也为分式
不用化简只看形式
分式有意义的条件
二
问题3.已知分式 请你计算分式的值。
对于分式
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
分式有意义的条件
······ 3 2 1 ······
······ ······
0
0
-1
无意义
例1:下列分式中的字母满足什么条件时分式有意义?
(2)当x 时,分式 有意义;
x≠y
(1)当a 时,分式 有意义;
(3)当m 时,分式 有意义;
(4)当 时,分式 有意义.
做一做:
(5)当b 时,分式 有意义.
(6)当x 时,分式 有意义.
(2)当x 时,分式 有意义;
为任意实数
拓展练习:
(1)当x 时,分式 有意义;
变式训练
(1)当 时,分式 的值为零.
想一想:分式 的值为零应满足什么条件?
当A=0而 B≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
分式值为零的条件
三
x=2
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴ 解得x=2.
三二
随堂练习
1.下列代数式中,属于分式的有( )
A. B. C. D.
C
2.当a=-1时,分式 的值( )
A.没有意义 B.等于零 C.等于1 D.等于-1
A
3.当x为任意实数时,下列分式一定有意义的是( )
A.
B.
C.
D.
B
课堂小结
分式
定义
值为零的条件
有意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子 叫做分式 ,其中,A叫做分式的分子,B叫做分式的分母.
分式 有意义的条件是B ≠0.
分式 值为零的条件是A=0且B ≠0.
