2022-2023学年华师大版数学九年级上册 22.2.5 一元二次方程根与系数的关系 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年华师大版数学九年级上册 22.2.5 一元二次方程根与系数的关系 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 743.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 15:39:58 | ||
图片预览





文档简介
(共19张PPT)
22.2.5 一元二次方程根与系数的关系
教学目标
(一)知识与技能:要求学生在理解的基础上掌握一元二次方程根与系数的关系式,能运用根与系数的关系由已知一元二次方程的一个根求出另一个根与未知数,会求一 元二次方程两个根的倒数和与平方和,两根之差.
(二)过程与方法:通过韦达定理的教学过程,使学生经历观察、实验、猜想、证明等数学活动过程,发展推理能力,能有条理地、清晰地阐述自己的观点,进一步培养学生的创新意识和创新精神.
(三)情感态度与价值观:通过情境教学过程,激发学生的求知欲望,培养学生积极学习数学的态度,体验数学活动中充满着探索与创造,体验数学活动中的成功感,建立自信心.
教学重难点
重点:一元二次方程根与系数的关系.
难点:让学生从具体方程的根发现一元二次方程根与系数之间的关系,并用语言表述.
温故知新
1.一元二次方程的一般形式是什么?ax2+bx+c=0(a≠0)
2.一元二次方程的求根公式是什么?
(b2-4ac≥0)
3.一元二次方程的根的情况怎样确定?
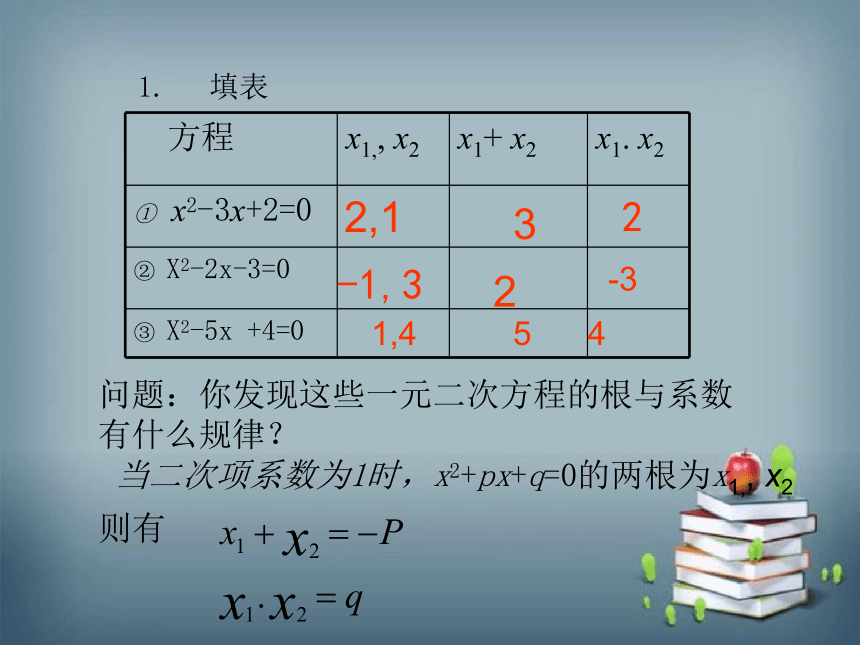
1. 填表
方程 x1,, x2 x1+ x2 x1. x2
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
问题:你发现这些一元二次方程的根与系数
有什么规律?
当二次项系数为1时,x2+px+q=0的两根为x1,, x2
则有
2,1
3
2
-1,3
2
-3
1,4
5
4
方程
1
-2
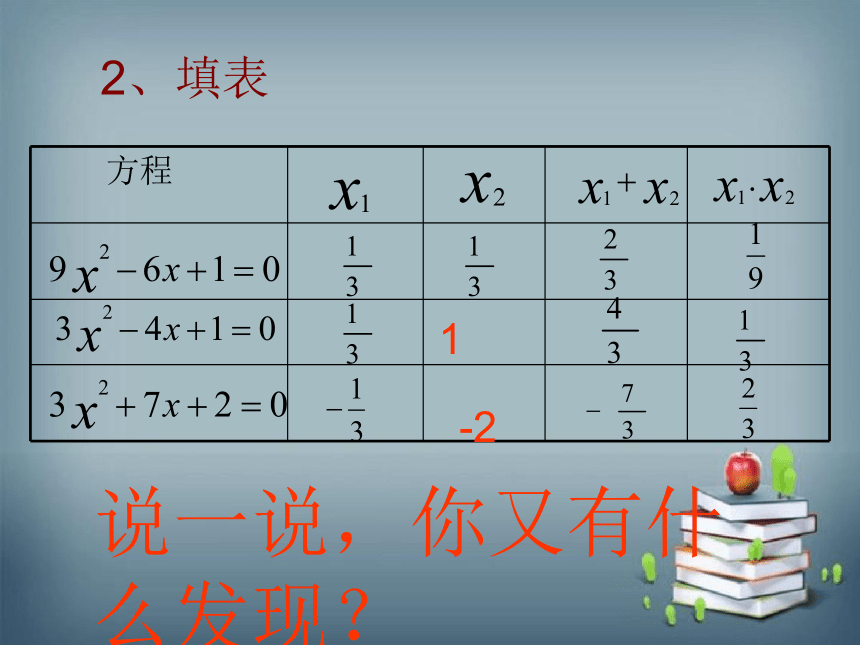
2、填表
说一说,你又有什么发现?
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a=0 , )的两根为x1= x2= ,则
,x1.x2与系数a,b,c 的关系为
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0 , )的两根为x1 , x2 则 x1.x2与系数a,b,c 的关系为
根与系数的关系
任意的一元二次方程ax2+bx+c=0(a≠0 )的两根为x1, x2,则x1+x2 ,x1.x2与系数a,b,c 的关系是: x1+x2=-— x1.x2= —
a
b
a
c
一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.
1、写出下列方程的两根和与两根积:
2、教材P35练习第2题
自学检测
写出下列方程的两根和与两根积
已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。
答:方程的另一个根是 k的值是7。
解:设方程的另一根为 ,则
已知方程 x2=2x+1的两根为x1, x2,
不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23
(3)
24
-10
-40
1、一元二次方程的一般形式 。
ax2+bx+c=0 (a≠0)
(1)a≠0
(2)△≥0
2、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1 、x2,
则x1+x2= ,x1x2= 。
3、用根与系数关系解题的条件是 。
一、知识要点:
要点归纳二
公式变形的特征。
x -y =(x+y)(x-y)
x +2xy+y =(x+y)
x -2xy+y =(x-y)
x +y =(x+y) -2xy
(x-y) =(x+y) -4xy
2、已知方程 的一
个根是2,求它的另一个根及 K 的值。
3、设 x1、x2 是方程 的
两个根,不解方程,
求下列各式的值。
(1)、(X1+1)(X2+1)
、 x1 X2
(2)、 (3)▁ + ▁
x2 X1
1 已知关于x的方程x2-px+q=0的
两个根是0和-3,求p和 q的值.
强化训练
课堂小结
1.本节课你有哪些收获?
2.还有没解决的问题吗?
22.2.5 一元二次方程根与系数的关系
教学目标
(一)知识与技能:要求学生在理解的基础上掌握一元二次方程根与系数的关系式,能运用根与系数的关系由已知一元二次方程的一个根求出另一个根与未知数,会求一 元二次方程两个根的倒数和与平方和,两根之差.
(二)过程与方法:通过韦达定理的教学过程,使学生经历观察、实验、猜想、证明等数学活动过程,发展推理能力,能有条理地、清晰地阐述自己的观点,进一步培养学生的创新意识和创新精神.
(三)情感态度与价值观:通过情境教学过程,激发学生的求知欲望,培养学生积极学习数学的态度,体验数学活动中充满着探索与创造,体验数学活动中的成功感,建立自信心.
教学重难点
重点:一元二次方程根与系数的关系.
难点:让学生从具体方程的根发现一元二次方程根与系数之间的关系,并用语言表述.
温故知新
1.一元二次方程的一般形式是什么?ax2+bx+c=0(a≠0)
2.一元二次方程的求根公式是什么?
(b2-4ac≥0)
3.一元二次方程的根的情况怎样确定?
1. 填表
方程 x1,, x2 x1+ x2 x1. x2
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
问题:你发现这些一元二次方程的根与系数
有什么规律?
当二次项系数为1时,x2+px+q=0的两根为x1,, x2
则有
2,1
3
2
-1,3
2
-3
1,4
5
4
方程
1
-2
2、填表
说一说,你又有什么发现?
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a=0 , )的两根为x1= x2= ,则
,x1.x2与系数a,b,c 的关系为
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0 , )的两根为x1 , x2 则 x1.x2与系数a,b,c 的关系为
根与系数的关系
任意的一元二次方程ax2+bx+c=0(a≠0 )的两根为x1, x2,则x1+x2 ,x1.x2与系数a,b,c 的关系是: x1+x2=-— x1.x2= —
a
b
a
c
一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.
1、写出下列方程的两根和与两根积:
2、教材P35练习第2题
自学检测
写出下列方程的两根和与两根积
已知方程 2x2+kx-4=0的一个根是-4,求它的另一个根及k的值。
答:方程的另一个根是 k的值是7。
解:设方程的另一根为 ,则
已知方程 x2=2x+1的两根为x1, x2,
不解方程,求下列各式的值。
(1)(x1-x2)2 (2)x13x2+x1x23
(3)
24
-10
-40
1、一元二次方程的一般形式 。
ax2+bx+c=0 (a≠0)
(1)a≠0
(2)△≥0
2、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1 、x2,
则x1+x2= ,x1x2= 。
3、用根与系数关系解题的条件是 。
一、知识要点:
要点归纳二
公式变形的特征。
x -y =(x+y)(x-y)
x +2xy+y =(x+y)
x -2xy+y =(x-y)
x +y =(x+y) -2xy
(x-y) =(x+y) -4xy
2、已知方程 的一
个根是2,求它的另一个根及 K 的值。
3、设 x1、x2 是方程 的
两个根,不解方程,
求下列各式的值。
(1)、(X1+1)(X2+1)
、 x1 X2
(2)、 (3)▁ + ▁
x2 X1
1 已知关于x的方程x2-px+q=0的
两个根是0和-3,求p和 q的值.
强化训练
课堂小结
1.本节课你有哪些收获?
2.还有没解决的问题吗?
