人教版数学八年级上册 12.1全等三角形 课件 (共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.1全等三角形 课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 16:36:54 | ||
图片预览







文档简介
(共25张PPT)
能够完全重合的两个图形叫做全等形
观察下面两组图形,它们是不是全等图形?为什么?
(1)
(2)
如果两个图形全等,它们的形状一定相同、大小一定相等 !
定义:能够完全重合的两个三角形叫_________
全等三角形
把两个全等的三角形重合到一起,重合的顶
点叫做对应顶点,
重合的
角叫做对应角。
重合的边叫做对应边,
其中点A和__,点B和__,点C和__是对应顶点。
AB和___,BC和___,AC和___是对应边。
∠A和___ ,∠B和___, ∠C和___ 是对应角。
D
E
F
DE
EF
DF
∠D
∠E
∠F
A
B
C
D
E
F
“全等”用符号“≌”表示,读作“全等于”
如上图:△ ABC全等于△DEF记作:△ ABC ≌ △DEF
(注意:书写时应把对应顶点写在相对应的位置上)
A
B
C
D
E
F
ABC≌ DEF,对应边大小有什么关系?
对应角呢?
A
B
C
D
E
F
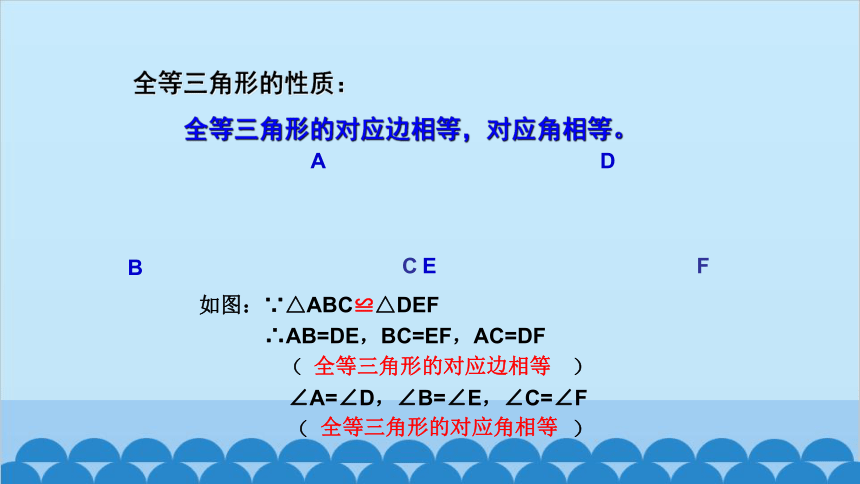
全等三角形的性质:
全等三角形的对应边相等,对应角相等。
如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∠A=∠D,∠B=∠E,∠C=∠F
( )
全等三角形的对应边相等
全等三角形的对应角相等
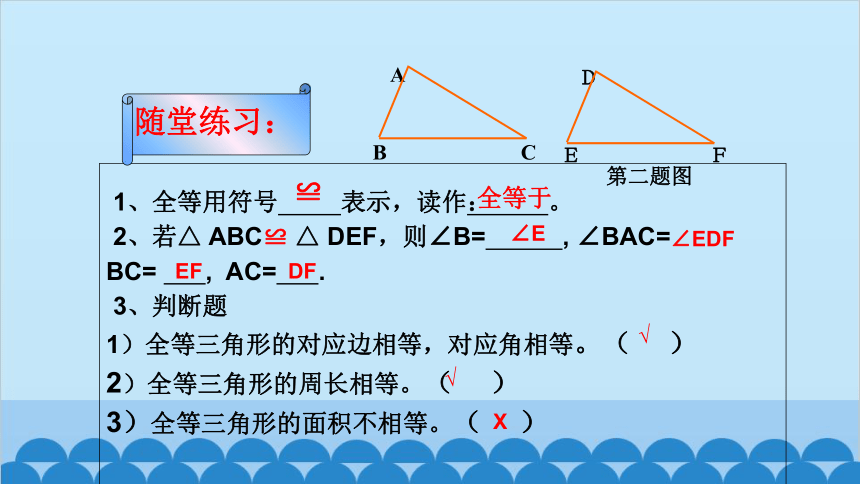
1、全等用符号 表示,读作: 。
2、若△ ABC≌ △ DEF,则∠B= , ∠BAC= BC= , AC= .
3、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等。( )
3)全等三角形的面积不相等。( )
随堂练习:
≌
全等于
∠E
EF
DF
∠EDF
√
√
X
A
C
B
D
F
E
第二题图
A
A
C
B
D
E
图1
图2
图3
图4
A
B
D
C
A
B
C
D
B
C
N
M
F
E
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
C
B
图1
图2
图3
图4
图5
A
B
D
C
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
D
E
观察
1、如图1,已知△ABC≌△DBC,则BC的对应边是 。
请按要求找出对应边或对应角。
A
C
B
D
图1
A
C
B
E
D
图2
A
B
C
F
D
E
图4
2、如图2,已知△ABE≌△ACD,则∠ A 的对应角是 。
两个全等三角形的公共边一定为对应边。
3、如图3,已知△ABC≌△ADE,则∠ 1 的对应角是 。
A
B
C
D
E
图3
1
2
两个全等三角形的公共角或对顶角一定为对应角。
4、如图4,已知△ABC≌△DEF,则BC、AC的对应边分别是 。
∠ A 、∠ B 的对应角分别是 。
两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角。
BC
EF、DF
∠ A
∠ 2
∠ D 、∠ E
小试身手
问题一:下列说法是否正确:
(1)同一面中华人民共和国国旗上,4个小五角星都是全等形。
×
√
(4)半径相等的两个圆是全等形。
√
(2)全等三角形的周长相等,面积也相等。
(3)周长相等的两个三角形是全等三角形。
√
A
B
C
D
E
F
全等三角形的性质:
全等三角形的对应边相等,对应角相等。
如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∴∠A=∠D,∠B=∠E,∠C=∠F
( )
全等三角形的对应边相等
全等三角形的对应角相等
已知△ABD ≌ △EBC 且AB=3cm,DE=2cm,求BC的长.
A
B
C
D
E
∴BE=3cm
解:∵△ABD ≌ △EBC
∴AB=BE,BC=BD ( )
∵AB=3cm
∴BC=BD=DE+BE =2+3=5cm
小试牛刀
如图,△ABD≌△ACE,若∠ADB=100O, ∠B=30O,你能说出△ACE中各角的大小吗?
A
B
C
D
E
解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=100O ,∠C= ∠B=30O,
又∵∠A+∠AEC+∠C=180°
∴∠A=180O- ∠AEC- ∠C
=180O-100O-30O=50O
4
3
1
2
A
C
B
D
如图△ABC≌ △CDA,AB和CD、BC和DA是对应边,说出对应角和另外一组对应边,以下是李华同学的解答过程,你认为对吗?如果不对,正确的答案是什么?
解:∵△ABC≌△CDA
∴∠1与∠ 2,∠3与∠4,∠B与∠D是对应角
AC与AC对应边
做错啦!!
想想看:上题中边AB、CD位置上有什么关系?
例1.如图, △ABC≌△ADE,∠C=50°,∠D=45°,
∠CFA=75°,求∠ BAC和∠BAE的度数。
A
B
C
D
E
F
随堂练习
1、如图,已知△ABC≌△ADE,∠C=∠E,BC=DE,其它的对应边有:_________________,对应角有:____________________.
E
D
B
C
A
随堂练习
2、如图,已知△ABC≌ △ADE,若∠D= ∠B,∠C= ∠AED,则∠DAE=___________; ∠DAB=___________.
E
D
B
C
A
随堂练习
3、如图△ABD≌△CDB,若AB=4,AD=5,BD=6,求△CDB的周长。
A
B
D
C
随堂练习
4、如图△ABD≌△EBC,AB=3cm,AC=8cm,求DE的长。
C
E
A
B
D
5. 如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,AD=7cm,DM=5cm, ∠DAM=39°,则△ANM≌△ ADM AN=___cm,
NM=___cm,
∠NAB=___.
M
D
A
N
B
C
7cm
5 cm
)39°
7
5
12。
思考题:把四边形ABCD纸片沿EF折叠使
点C落在四边形ABCD内部,如图,则
∠C与∠1+∠2之间的一种数量关系
始终保持不变,这个规律是( )
∠C=∠1+∠2
2∠C=∠1+∠2
3∠C=∠1+∠2
3∠C=2(∠1+∠2)
A
B
C
D
1
2
E
F
C′
B
能够完全重合的两个图形叫做全等形
观察下面两组图形,它们是不是全等图形?为什么?
(1)
(2)
如果两个图形全等,它们的形状一定相同、大小一定相等 !
定义:能够完全重合的两个三角形叫_________
全等三角形
把两个全等的三角形重合到一起,重合的顶
点叫做对应顶点,
重合的
角叫做对应角。
重合的边叫做对应边,
其中点A和__,点B和__,点C和__是对应顶点。
AB和___,BC和___,AC和___是对应边。
∠A和___ ,∠B和___, ∠C和___ 是对应角。
D
E
F
DE
EF
DF
∠D
∠E
∠F
A
B
C
D
E
F
“全等”用符号“≌”表示,读作“全等于”
如上图:△ ABC全等于△DEF记作:△ ABC ≌ △DEF
(注意:书写时应把对应顶点写在相对应的位置上)
A
B
C
D
E
F
ABC≌ DEF,对应边大小有什么关系?
对应角呢?
A
B
C
D
E
F
全等三角形的性质:
全等三角形的对应边相等,对应角相等。
如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∠A=∠D,∠B=∠E,∠C=∠F
( )
全等三角形的对应边相等
全等三角形的对应角相等
1、全等用符号 表示,读作: 。
2、若△ ABC≌ △ DEF,则∠B= , ∠BAC= BC= , AC= .
3、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等。( )
3)全等三角形的面积不相等。( )
随堂练习:
≌
全等于
∠E
EF
DF
∠EDF
√
√
X
A
C
B
D
F
E
第二题图
A
A
C
B
D
E
图1
图2
图3
图4
A
B
D
C
A
B
C
D
B
C
N
M
F
E
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
B
A
C
N
P
M
A
C
B
D
E
A
B
C
D
C
B
图1
图2
图3
图4
图5
A
B
D
C
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
D
E
观察
1、如图1,已知△ABC≌△DBC,则BC的对应边是 。
请按要求找出对应边或对应角。
A
C
B
D
图1
A
C
B
E
D
图2
A
B
C
F
D
E
图4
2、如图2,已知△ABE≌△ACD,则∠ A 的对应角是 。
两个全等三角形的公共边一定为对应边。
3、如图3,已知△ABC≌△ADE,则∠ 1 的对应角是 。
A
B
C
D
E
图3
1
2
两个全等三角形的公共角或对顶角一定为对应角。
4、如图4,已知△ABC≌△DEF,则BC、AC的对应边分别是 。
∠ A 、∠ B 的对应角分别是 。
两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角。
BC
EF、DF
∠ A
∠ 2
∠ D 、∠ E
小试身手
问题一:下列说法是否正确:
(1)同一面中华人民共和国国旗上,4个小五角星都是全等形。
×
√
(4)半径相等的两个圆是全等形。
√
(2)全等三角形的周长相等,面积也相等。
(3)周长相等的两个三角形是全等三角形。
√
A
B
C
D
E
F
全等三角形的性质:
全等三角形的对应边相等,对应角相等。
如图:∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF
( )
∴∠A=∠D,∠B=∠E,∠C=∠F
( )
全等三角形的对应边相等
全等三角形的对应角相等
已知△ABD ≌ △EBC 且AB=3cm,DE=2cm,求BC的长.
A
B
C
D
E
∴BE=3cm
解:∵△ABD ≌ △EBC
∴AB=BE,BC=BD ( )
∵AB=3cm
∴BC=BD=DE+BE =2+3=5cm
小试牛刀
如图,△ABD≌△ACE,若∠ADB=100O, ∠B=30O,你能说出△ACE中各角的大小吗?
A
B
C
D
E
解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=100O ,∠C= ∠B=30O,
又∵∠A+∠AEC+∠C=180°
∴∠A=180O- ∠AEC- ∠C
=180O-100O-30O=50O
4
3
1
2
A
C
B
D
如图△ABC≌ △CDA,AB和CD、BC和DA是对应边,说出对应角和另外一组对应边,以下是李华同学的解答过程,你认为对吗?如果不对,正确的答案是什么?
解:∵△ABC≌△CDA
∴∠1与∠ 2,∠3与∠4,∠B与∠D是对应角
AC与AC对应边
做错啦!!
想想看:上题中边AB、CD位置上有什么关系?
例1.如图, △ABC≌△ADE,∠C=50°,∠D=45°,
∠CFA=75°,求∠ BAC和∠BAE的度数。
A
B
C
D
E
F
随堂练习
1、如图,已知△ABC≌△ADE,∠C=∠E,BC=DE,其它的对应边有:_________________,对应角有:____________________.
E
D
B
C
A
随堂练习
2、如图,已知△ABC≌ △ADE,若∠D= ∠B,∠C= ∠AED,则∠DAE=___________; ∠DAB=___________.
E
D
B
C
A
随堂练习
3、如图△ABD≌△CDB,若AB=4,AD=5,BD=6,求△CDB的周长。
A
B
D
C
随堂练习
4、如图△ABD≌△EBC,AB=3cm,AC=8cm,求DE的长。
C
E
A
B
D
5. 如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,AD=7cm,DM=5cm, ∠DAM=39°,则△ANM≌△ ADM AN=___cm,
NM=___cm,
∠NAB=___.
M
D
A
N
B
C
7cm
5 cm
)39°
7
5
12。
思考题:把四边形ABCD纸片沿EF折叠使
点C落在四边形ABCD内部,如图,则
∠C与∠1+∠2之间的一种数量关系
始终保持不变,这个规律是( )
∠C=∠1+∠2
2∠C=∠1+∠2
3∠C=∠1+∠2
3∠C=2(∠1+∠2)
A
B
C
D
1
2
E
F
C′
B
