2022-2023学年数学华师大版九年级上册 23.3.4 相似三角形的应用 课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年数学华师大版九年级上册 23.3.4 相似三角形的应用 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 16:26:29 | ||
图片预览




文档简介
(共18张PPT)
23.3.4 相似三角形的应用
教学目标
1、进一步巩固相似三角形的知识,让学生学会运用两个三角形相似解决实际问题;能够运用三角形相似的知识,解决不能直接测量的物体的长度和高度等一些实际问题。
2、通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模思想,培养学生分析问题、解决问题、观察、归纳、建模、应用能力。
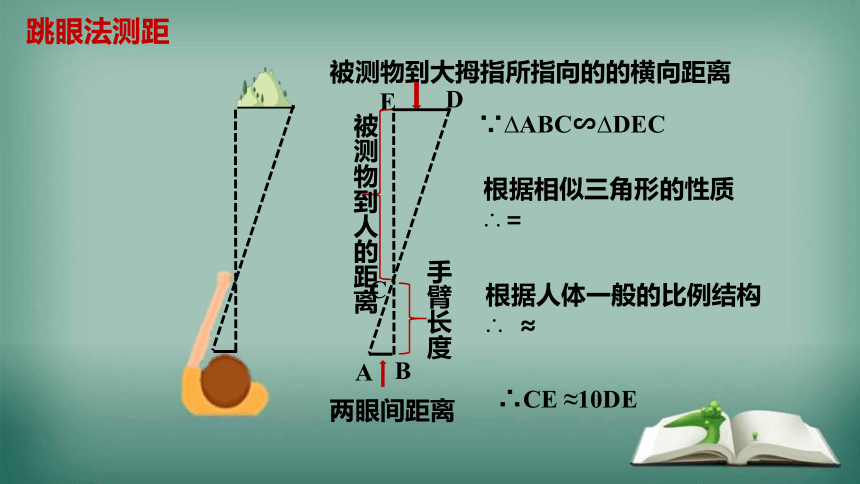
跳眼法测距
A
D
B
E
C
∵ ABC∽ DEC
根据相似三角形的性质
∴=
根据人体一般的比例结构
∴ ≈
∴CE ≈10DE
两眼间距离
手臂长度
被测物到人的距离
被测物到大拇指所指向的的横向距离
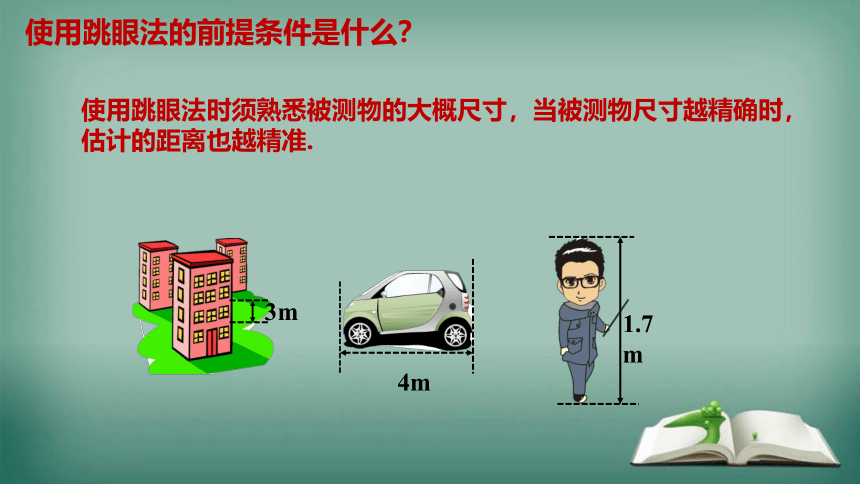
3m
4m
1.7m
使用跳眼法时须熟悉被测物的大概尺寸,当被测物尺寸越精确时,估计的距离也越精准.
使用跳眼法的前提条件是什么?
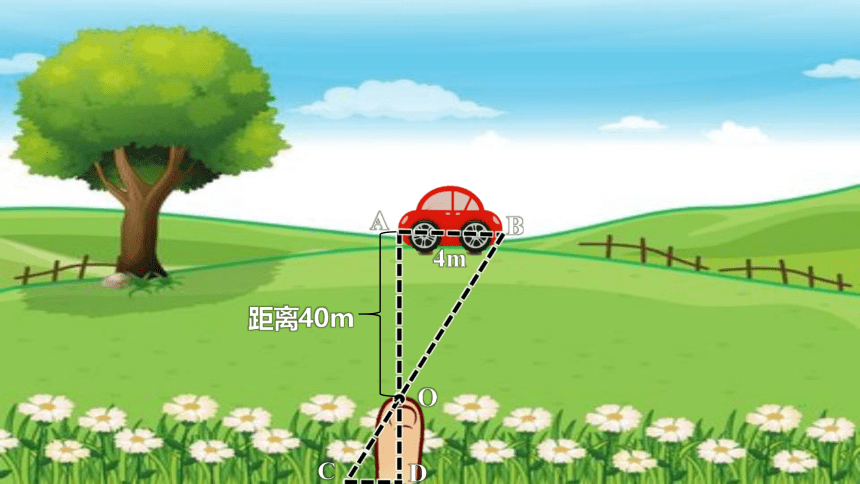
B
A
O
4m
距离40m
C
D
利用太阳光测量物体高度
问题1:活动中用到的工具有哪些?
问题2:活动中需要测量哪些数据?
标杆和米尺
石峰的影长和标杆的影长
问题3:已知:标杆长2米,石峰影长6.34米,标杆影长2.56米,你能求出石峰的高度吗?(结果精确到0.01)
∵AC//DF
又∵∠E=∠CBA=90 °
∴ ABC∽ DEF
∴=
∴=
6.34m
2.56m
C
B
D
A
E
F
2m
数学建模
∴BC≈4.95m
∴∠A=∠EDF
∵AB=6.34m,DE=2.56m,EF=2m
利用平面镜
测量物体高度
问题1:活动中用到的工具有哪些?
问题2:活动中需要测量哪些数据?
平面镜和米尺
1.脚中间位置与镜子中间位置的距离
2.镜子中间位置与灯杆底座中间位置的距离
问题3:已知观测者的眼睛到地面的距离为1.81米;
脚中间位置与镜子中间位置的距离0.76米;
镜子中间位置与灯杆底座中间位置的距离2.47米,
你能求出灯杆的高度吗? (结果精确到0.01)
A
D
B
C
E
且∠B=∠D=90 °
∴ ABC∽ EDC
∴=
∴=
∴DE≈5.88m
∵∠ACB=∠ECD
∵AB=1.81m,BC=0.76m,CD=2.47m
数学建模
能力提升
某校九年级数学兴趣小组的活动课题是“测量物体高度”,小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度,以下是他们研究报告的部分记录内容:
课题 测量古塔的高度 小明的研究报告 小红的研究报告
测量工具 标杆(2米)、皮尺 平面镜、皮尺
测量方案及测量数据 利用太阳光线,在同一时刻测得标杆的影长3.2米,古塔的影长44米,已知标杆的长度2米 人的身高1.75米,人脚中间位置与平面镜中间位置的距离2.4米,镜子中间位置与古塔边缘的距离35米
画出图示
计算过程(计算结果精确到0.1)
2.55米
2.75米
能力提升
课题 测量古塔的高度 小明的研究报告 小红的研究报告
测量工具 标杆(2米)、皮尺 平面镜、皮尺
图示
测量方案及测量数据 利用太阳光线,在同一时刻测得标杆的影长AB为3.2米,古塔的影长AD为44米,已知标杆的长度BC为2米 人的身高AB为1.75米,人脚中间位置与平面镜中间位置的距离AC为2.4米,镜子中间位置与古塔边缘的距离为35米
计算过程(计算结果精确到0.1)
E
C
B
D
A
A
B
C
D
E
2.75米
2.55米
当堂检测
1.某一时记得,身高1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得某旗杆的影长为5m,则该旗杆的高度是( )
A、1.25m B、10m C、20m D、8m
2.如图是小玲设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米,那么该古城墙的高度CD是 米。
C
8
3.如图,为了估算河的宽度,我们可以在河对岸选定一定A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=70米,请你求出小河的宽度是多少米?
解:∵ AB⊥BC ,EC⊥BC
∴ ∠B = ∠C =90 °
∵ ∠ADB = ∠CDE
∴△ABD ∽△CED
∴=
∵ BD=180 , DC=60, EC=70
∴=
∴AB=210米
4.铁道口栏杆的短臂长为0.8米,长臂长为8米,当短臂端点下降0.4米时,长臂端点升高多少米?(杆的粗细忽略不计).
A
B
C
D
O
解:∵ ∠ABO = ∠CDO =90 °
且 ∠AOB = ∠COD
∴△ABO ∽△CDO
∴=
∵ AO=0.8 , OC=8, AB=0.4
∴=
∴AB=4米
∴长臂端点升高4米
相似三角形应用
测距
测高
跳眼法
利用太阳光线
利用平面镜
熟悉被测物大概尺寸
入射角等于反射角
同一时刻物高与影长成正比
23.3.4 相似三角形的应用
教学目标
1、进一步巩固相似三角形的知识,让学生学会运用两个三角形相似解决实际问题;能够运用三角形相似的知识,解决不能直接测量的物体的长度和高度等一些实际问题。
2、通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模思想,培养学生分析问题、解决问题、观察、归纳、建模、应用能力。
跳眼法测距
A
D
B
E
C
∵ ABC∽ DEC
根据相似三角形的性质
∴=
根据人体一般的比例结构
∴ ≈
∴CE ≈10DE
两眼间距离
手臂长度
被测物到人的距离
被测物到大拇指所指向的的横向距离
3m
4m
1.7m
使用跳眼法时须熟悉被测物的大概尺寸,当被测物尺寸越精确时,估计的距离也越精准.
使用跳眼法的前提条件是什么?
B
A
O
4m
距离40m
C
D
利用太阳光测量物体高度
问题1:活动中用到的工具有哪些?
问题2:活动中需要测量哪些数据?
标杆和米尺
石峰的影长和标杆的影长
问题3:已知:标杆长2米,石峰影长6.34米,标杆影长2.56米,你能求出石峰的高度吗?(结果精确到0.01)
∵AC//DF
又∵∠E=∠CBA=90 °
∴ ABC∽ DEF
∴=
∴=
6.34m
2.56m
C
B
D
A
E
F
2m
数学建模
∴BC≈4.95m
∴∠A=∠EDF
∵AB=6.34m,DE=2.56m,EF=2m
利用平面镜
测量物体高度
问题1:活动中用到的工具有哪些?
问题2:活动中需要测量哪些数据?
平面镜和米尺
1.脚中间位置与镜子中间位置的距离
2.镜子中间位置与灯杆底座中间位置的距离
问题3:已知观测者的眼睛到地面的距离为1.81米;
脚中间位置与镜子中间位置的距离0.76米;
镜子中间位置与灯杆底座中间位置的距离2.47米,
你能求出灯杆的高度吗? (结果精确到0.01)
A
D
B
C
E
且∠B=∠D=90 °
∴ ABC∽ EDC
∴=
∴=
∴DE≈5.88m
∵∠ACB=∠ECD
∵AB=1.81m,BC=0.76m,CD=2.47m
数学建模
能力提升
某校九年级数学兴趣小组的活动课题是“测量物体高度”,小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度,以下是他们研究报告的部分记录内容:
课题 测量古塔的高度 小明的研究报告 小红的研究报告
测量工具 标杆(2米)、皮尺 平面镜、皮尺
测量方案及测量数据 利用太阳光线,在同一时刻测得标杆的影长3.2米,古塔的影长44米,已知标杆的长度2米 人的身高1.75米,人脚中间位置与平面镜中间位置的距离2.4米,镜子中间位置与古塔边缘的距离35米
画出图示
计算过程(计算结果精确到0.1)
2.55米
2.75米
能力提升
课题 测量古塔的高度 小明的研究报告 小红的研究报告
测量工具 标杆(2米)、皮尺 平面镜、皮尺
图示
测量方案及测量数据 利用太阳光线,在同一时刻测得标杆的影长AB为3.2米,古塔的影长AD为44米,已知标杆的长度BC为2米 人的身高AB为1.75米,人脚中间位置与平面镜中间位置的距离AC为2.4米,镜子中间位置与古塔边缘的距离为35米
计算过程(计算结果精确到0.1)
E
C
B
D
A
A
B
C
D
E
2.75米
2.55米
当堂检测
1.某一时记得,身高1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得某旗杆的影长为5m,则该旗杆的高度是( )
A、1.25m B、10m C、20m D、8m
2.如图是小玲设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米,那么该古城墙的高度CD是 米。
C
8
3.如图,为了估算河的宽度,我们可以在河对岸选定一定A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=70米,请你求出小河的宽度是多少米?
解:∵ AB⊥BC ,EC⊥BC
∴ ∠B = ∠C =90 °
∵ ∠ADB = ∠CDE
∴△ABD ∽△CED
∴=
∵ BD=180 , DC=60, EC=70
∴=
∴AB=210米
4.铁道口栏杆的短臂长为0.8米,长臂长为8米,当短臂端点下降0.4米时,长臂端点升高多少米?(杆的粗细忽略不计).
A
B
C
D
O
解:∵ ∠ABO = ∠CDO =90 °
且 ∠AOB = ∠COD
∴△ABO ∽△CDO
∴=
∵ AO=0.8 , OC=8, AB=0.4
∴=
∴AB=4米
∴长臂端点升高4米
相似三角形应用
测距
测高
跳眼法
利用太阳光线
利用平面镜
熟悉被测物大概尺寸
入射角等于反射角
同一时刻物高与影长成正比
