2022年秋鲁教版(五四制)数学九年级上册 3.6 二次函数的应用 课件(共22张PPT)
文档属性
| 名称 | 2022年秋鲁教版(五四制)数学九年级上册 3.6 二次函数的应用 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
3.6 二次函数的应用
1、掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2、学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题
3.熟练应用二次函数的知识解决实际问题。
4.通过对实际问题的分析,建立二次函数的模型,解决实际问题。
重点:应用二次函数解决图形有关的最值问题
难点:求出二次函数的表达式
2 . 二次函数y=ax2+bx+c的图象是一条 ,它的对称
轴是 ,顶点坐标是 . 当a>0时,抛
物线开口向 ,有最 点,函数有最 值,是 ;当
a<0时,抛物线开口向 ,有最 点,函数有最 值,
是 。
抛物线
上
小
下
大
高
低
1. 二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 .
抛物线
直线x=h
(h,k)
河上有座抛物线拱桥,如图所示,拱顶离水面高2m时,测得水面宽4m,若想了解水面宽度变化时.拱顶离水面高度怎样变化,你能建立模型来解决这个问题吗?
A
B
C
D
标突
标突
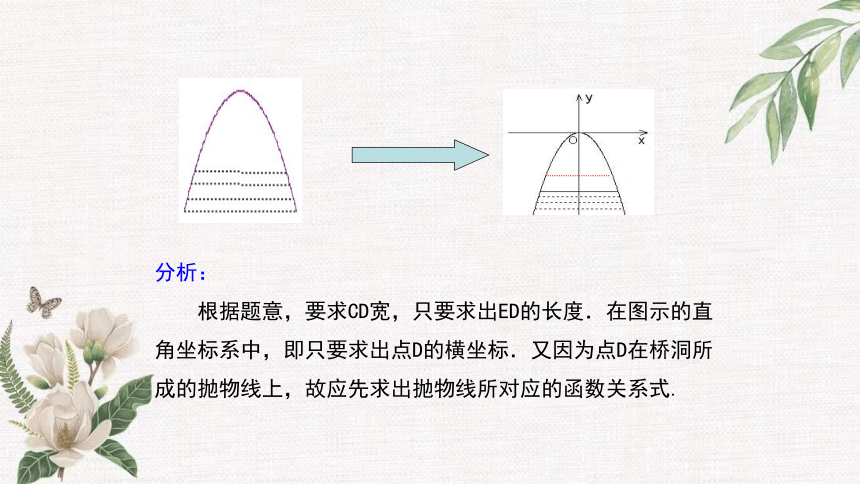
分析:
根据题意,要求CD宽,只要求出ED的长度.在图示的直角坐标系中,即只要求出点D的横坐标.又因为点D在桥洞所成的抛物线上,故应先求出抛物线所对应的函数关系式.
C
D
A
B
E
一座拱桥的纵截面是抛物线的异端,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米,如图.想了解水面宽度变化时,拱顶离水面的高度怎样变化.
你能想出办法来吗?
4.9m
4m
2m
建立函数模型
这是什么样的函数呢?
拱桥的纵截面是抛物线应当是某个二次函数的图象
你能想出办法来吗?
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
-2
-4
2
1
-2
-1
A
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上由此得出
解得
因此, ,其中 |x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们可以了解到水面宽变化时,拱顶离水面高度怎样变化.
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时, ,从而
因此拱顶离水面高1.125m
你是否体会到:从实际问题建立起函数模型,对于解决问题是有效的?
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
问题1 二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由 a 的符号、对称轴的位置及自变量的取值范围决定.
问题2 当自变量 x 为全体实数时,二次函数 y = ax2 + bx + c 的最值是多少?
当 a>0 时,有 ,此时 ;
当 a<0 时,有 ,此时 .
问题3 当自变量 x 限定范围时,二次函数 y = ax2 + bx + c 的最值如何确定?
先判断 是否在限定范围内,若在,则二次函数在 x = 时取得一个最值,另一个最值需考察限定范围的端点处来决定;若不在,则根据二次函数的增减性确定其最值.
例1 求下列函数的最大值与最小值:
x
O
y
解:
-3
1
(1)
∴ 当 时,有
当 时,有
解:
O
x
y
1
-3
(2)
∴ 当 x = -3 时,有
∴ 当 -3≤x≤1 时 y 随着 x 的增大而减小.
当 x = 1 时,有
例2 某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B (1,2.25)
●
C
●
D
o
A
x
y
(0,1.25)
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
●B (1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
1、足球被从地面上踢起,它距地面的高度h(m)可用公式
h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
2、河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的表达式为 ,当水面离桥拱顶的高度DO 是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
C
3、如图1,在△ABC中, ∠B=90 °,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过 秒,四边形APQC的面积最小.
A
B
C
P
Q
图1
3
抽象
转化
数学问题
运用
数学知识
问题的解决
解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
实际问题
3.6 二次函数的应用
1、掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2、学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题
3.熟练应用二次函数的知识解决实际问题。
4.通过对实际问题的分析,建立二次函数的模型,解决实际问题。
重点:应用二次函数解决图形有关的最值问题
难点:求出二次函数的表达式
2 . 二次函数y=ax2+bx+c的图象是一条 ,它的对称
轴是 ,顶点坐标是 . 当a>0时,抛
物线开口向 ,有最 点,函数有最 值,是 ;当
a<0时,抛物线开口向 ,有最 点,函数有最 值,
是 。
抛物线
上
小
下
大
高
低
1. 二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 .
抛物线
直线x=h
(h,k)
河上有座抛物线拱桥,如图所示,拱顶离水面高2m时,测得水面宽4m,若想了解水面宽度变化时.拱顶离水面高度怎样变化,你能建立模型来解决这个问题吗?
A
B
C
D
标突
标突
分析:
根据题意,要求CD宽,只要求出ED的长度.在图示的直角坐标系中,即只要求出点D的横坐标.又因为点D在桥洞所成的抛物线上,故应先求出抛物线所对应的函数关系式.
C
D
A
B
E
一座拱桥的纵截面是抛物线的异端,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米,如图.想了解水面宽度变化时,拱顶离水面的高度怎样变化.
你能想出办法来吗?
4.9m
4m
2m
建立函数模型
这是什么样的函数呢?
拱桥的纵截面是抛物线应当是某个二次函数的图象
你能想出办法来吗?
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
-2
-4
2
1
-2
-1
A
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上由此得出
解得
因此, ,其中 |x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们可以了解到水面宽变化时,拱顶离水面高度怎样变化.
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时, ,从而
因此拱顶离水面高1.125m
你是否体会到:从实际问题建立起函数模型,对于解决问题是有效的?
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
问题1 二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由 a 的符号、对称轴的位置及自变量的取值范围决定.
问题2 当自变量 x 为全体实数时,二次函数 y = ax2 + bx + c 的最值是多少?
当 a>0 时,有 ,此时 ;
当 a<0 时,有 ,此时 .
问题3 当自变量 x 限定范围时,二次函数 y = ax2 + bx + c 的最值如何确定?
先判断 是否在限定范围内,若在,则二次函数在 x = 时取得一个最值,另一个最值需考察限定范围的端点处来决定;若不在,则根据二次函数的增减性确定其最值.
例1 求下列函数的最大值与最小值:
x
O
y
解:
-3
1
(1)
∴ 当 时,有
当 时,有
解:
O
x
y
1
-3
(2)
∴ 当 x = -3 时,有
∴ 当 -3≤x≤1 时 y 随着 x 的增大而减小.
当 x = 1 时,有
例2 某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B (1,2.25)
●
C
●
D
o
A
x
y
(0,1.25)
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
●B (1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
1、足球被从地面上踢起,它距地面的高度h(m)可用公式
h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
2、河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的表达式为 ,当水面离桥拱顶的高度DO 是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
C
3、如图1,在△ABC中, ∠B=90 °,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过 秒,四边形APQC的面积最小.
A
B
C
P
Q
图1
3
抽象
转化
数学问题
运用
数学知识
问题的解决
解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
实际问题
