2022年秋鲁教版(五四制)数学九年级上册 3.7 二次函数与一元二次方程 课件 (共18张PPT)
文档属性
| 名称 | 2022年秋鲁教版(五四制)数学九年级上册 3.7 二次函数与一元二次方程 课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 17:15:27 | ||
图片预览




文档简介
(共18张PPT)
3.7 二次函数与一元二次方程
1.知识与技能目标:理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,及何时方程有两个不等的实根,两个相等的实根和没有实根;理解一元二次方程的根就是二次函数y=h(h是实数)图象交点的横坐标.
2.过程与方法目标:体会二次函数与方程之间的联系;掌握用图象法求方程的近似根;
3.情感态度与价值观:培养学生热爱数学、主动探究的能力
1、二次函数与一元二次方程的关系的探索过程.
2、准确理解二次函数与一元二次方程的关系
.
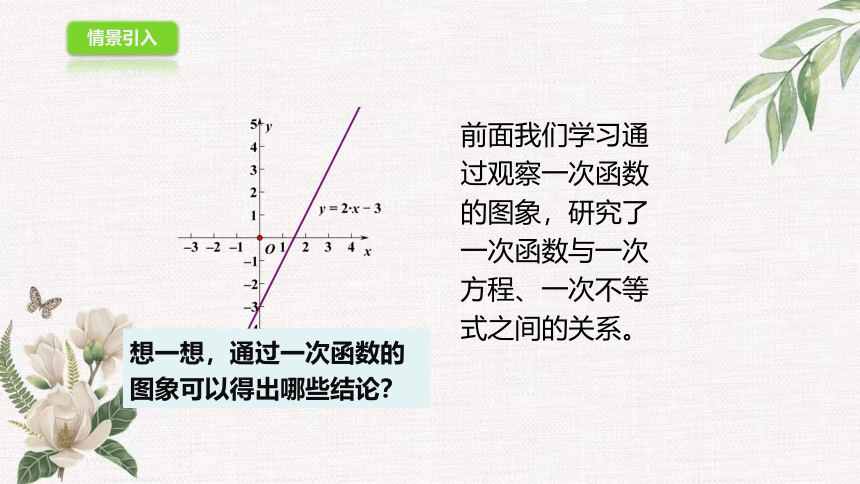
前面我们学习通过观察一次函数的图象,研究了一次函数与一次方程、一次不等式之间的关系。
想一想,通过一次函数的图象可以得出哪些结论?
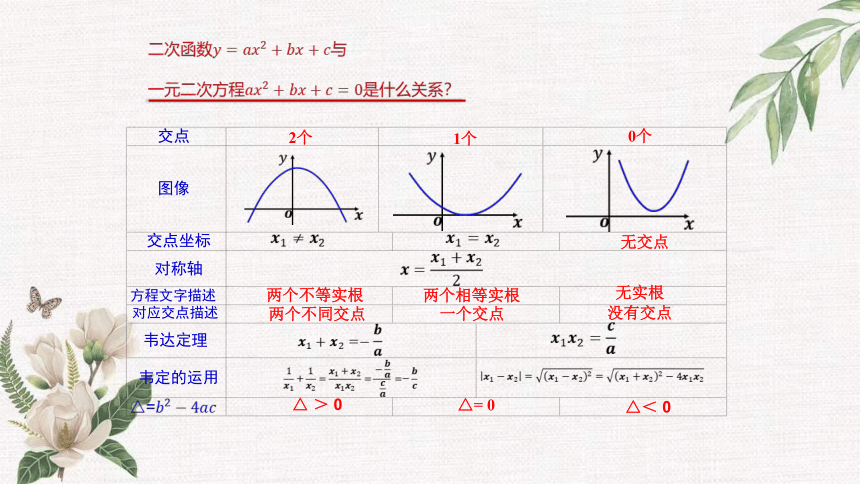
交点
图像
交点坐标
对称轴
方程文字描述
对应交点描述
韦达定理
韦定的运用
2个
1个
0个
无交点
两个不等实根
两个相等实根
无实根
两个不同交点
一个交点
没有交点
△ > 0
△= 0
△< 0
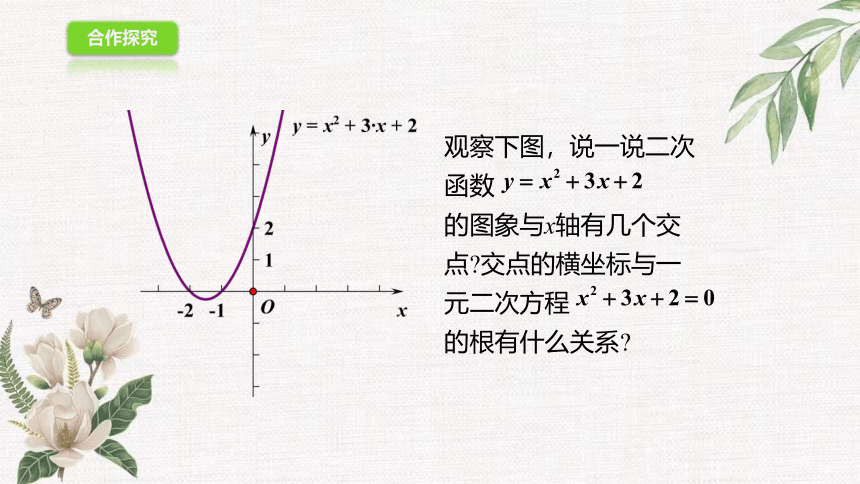
观察下图,说一说二次函数
的图象与x轴有几个交点 交点的横坐标与一元二次方程 的根有什么关系
观察图象可知,二次函数
的图象与x轴有两个交点。两交点分别为(-2,0)(-1,0),交点横坐标可看作是方程 的根。
根据上述问题3 画出的图象,继续回答下列问题:
(1)当x取何值时,y<0 当x取何值时,y>0
(2)试用含有x的不等式来描述问题(1)。
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
试一试
对于一元二次方程 ,
当 时有实数根,这个实数根就是对应二次函数
的值等于0时自变量x的一个值,即二次函数的图象与x轴一个交点的横坐标。
例 用图象法求一元二次方程x2+2x-1=0的近似解(精确到0.1).
由图象可知,方程有两个实数根,一个在-3和-2之间.另—个在0和1之间.
先求位于-3和-2之间的根.
x … -2.6 -2.5 -2.4 -2.3 …
y … …
0.56
0.25
-0.04
-0.31
观察x取何值时,y值最接近0?
先求位于-3和-2之间的根.
x … -2.6 -2.5 -2.4 -2.3 …
y … …
0.56
0.25
-0.04
-0.31
观察上表可以发现,当x分别取-2.5和-2.4时,对应的y由正变负,可见在-2.5与-2.4之间有一个x使y=0,即有方程 的一个根。
… -1 0 1 2 3 …
… -3 2 3 0 -7 …
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式
-x2+4x>2x的解集是 ( )
A.x<0 B.0C.0C
变 形
函数图象交点的横坐标
变 形
函数图象交点的横坐标
变形方式
3.7 二次函数与一元二次方程
1.知识与技能目标:理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,及何时方程有两个不等的实根,两个相等的实根和没有实根;理解一元二次方程的根就是二次函数y=h(h是实数)图象交点的横坐标.
2.过程与方法目标:体会二次函数与方程之间的联系;掌握用图象法求方程的近似根;
3.情感态度与价值观:培养学生热爱数学、主动探究的能力
1、二次函数与一元二次方程的关系的探索过程.
2、准确理解二次函数与一元二次方程的关系
.
前面我们学习通过观察一次函数的图象,研究了一次函数与一次方程、一次不等式之间的关系。
想一想,通过一次函数的图象可以得出哪些结论?
交点
图像
交点坐标
对称轴
方程文字描述
对应交点描述
韦达定理
韦定的运用
2个
1个
0个
无交点
两个不等实根
两个相等实根
无实根
两个不同交点
一个交点
没有交点
△ > 0
△= 0
△< 0
观察下图,说一说二次函数
的图象与x轴有几个交点 交点的横坐标与一元二次方程 的根有什么关系
观察图象可知,二次函数
的图象与x轴有两个交点。两交点分别为(-2,0)(-1,0),交点横坐标可看作是方程 的根。
根据上述问题3 画出的图象,继续回答下列问题:
(1)当x取何值时,y<0 当x取何值时,y>0
(2)试用含有x的不等式来描述问题(1)。
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
试一试
对于一元二次方程 ,
当 时有实数根,这个实数根就是对应二次函数
的值等于0时自变量x的一个值,即二次函数的图象与x轴一个交点的横坐标。
例 用图象法求一元二次方程x2+2x-1=0的近似解(精确到0.1).
由图象可知,方程有两个实数根,一个在-3和-2之间.另—个在0和1之间.
先求位于-3和-2之间的根.
x … -2.6 -2.5 -2.4 -2.3 …
y … …
0.56
0.25
-0.04
-0.31
观察x取何值时,y值最接近0?
先求位于-3和-2之间的根.
x … -2.6 -2.5 -2.4 -2.3 …
y … …
0.56
0.25
-0.04
-0.31
观察上表可以发现,当x分别取-2.5和-2.4时,对应的y由正变负,可见在-2.5与-2.4之间有一个x使y=0,即有方程 的一个根。
… -1 0 1 2 3 …
… -3 2 3 0 -7 …
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式
-x2+4x>2x的解集是 ( )
A.x<0 B.0
变 形
函数图象交点的横坐标
变 形
函数图象交点的横坐标
变形方式
