1.1.3 菱形的性质与判定的综合应用 课件(共20张PPT)
文档属性
| 名称 | 1.1.3 菱形的性质与判定的综合应用 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 978.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 07:49:54 | ||
图片预览








文档简介
(共20张PPT)
北师大版 九年级上册
1.1 菱形的性质与判定
第3课时 菱形的性质与判定的综合应用
情景导入
我们已经研究了一个特殊的平行四边形——菱形,它的定义是什么呢?有哪些性质呢?
问题1:菱形的定义:___________________________________
问题2:菱形的性质:
(边)__________________________
(角)__________________________
(对角线)_______________________________________________
(对称性)_______________________________________________
有一组邻边相等的平行四边形叫做菱形
对边平行且四条边相等
对角相等,邻角互补
对角线互相垂直平分,并且每条对角线平分一组对角
既是轴对称图形,也是中心对称图形
实践探究
探究1
如图,两张等宽的纸条交叉重叠在一起,重叠部分ABCD是菱形吗?为什么?
A
B
C
D
证明:∵等宽纸条对边平行,
∴AD∥BC, AB∥CD,∴□ABCD 是平行四边形,
从 A点作AM⊥DC 交于点 M,
作AN⊥BC交于点 N,
∵是两张等宽的纸,∴AM = AN.
∵□ABCD 是平行四边形,∴∠ABN=∠ADM,
∵AM⊥DC ,AN⊥BC,∴∠ANB =∠AMD = 90°,
∴△ABN≌△ADM,∴AB = AD,
∴四边形 ABCD 是菱形(一组邻边相等的平行四边形是菱形)
探究2
若纸条的宽度是3,∠ABC=60°,你会求菱形的面积吗?你有几种不同的方法?
A
B
C
D
方法一:菱形是特殊的平行四边形,可以用“底×高”求菱形的面积.
解:过点A作AE⊥BC于点E,
在Rt△ABE中,∠B=60°,AE=3,
设BE=x(x>0),则AB=2x.
由勾股定理,得AB2=AE2+BE2,
即(2x)2=32+x2,解得x= ,
∴BE= ,AB=2 ,
S菱形ABCD=BC·AE=2 ×3=6 .
A
B
C
D
E
方法二:菱形的对角线互相垂直,可以用 AC·BD,求菱形的面积.
解:连接AC,BD交于点O,过点A作AE⊥BC于点E.
∵四边形ABCD为菱形,∠ABC=60°,
∴△ABC是等边三角形.
由方法(1)可知AB=2 ,
∴AB=BC=AC=2 ,
A
B
C
D
O
E
∴OA= .
在Rt△AOB中,由勾股定理,得
OB= = =3,
∴BD=2OB=2×3=6.
S菱形ABCD=2S△ABC= AC·OB×2= AC·BD= ×2 ×6=6 .
A
B
C
D
O
E
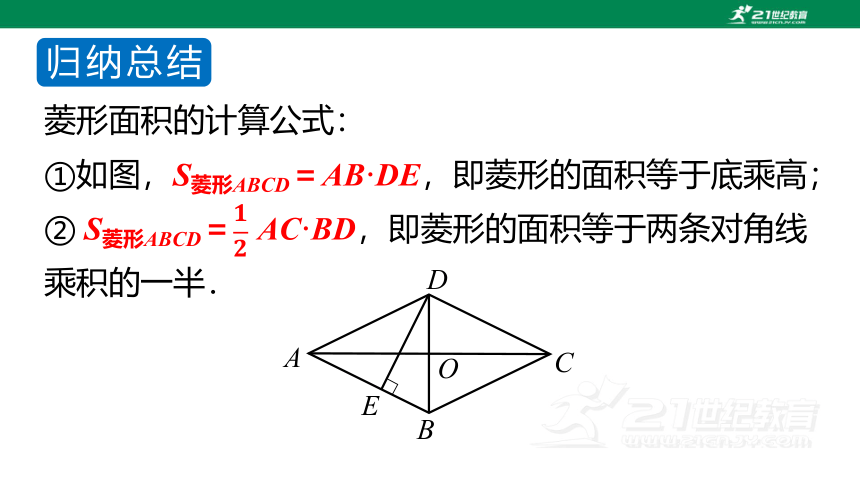
归纳总结
菱形面积的计算公式:
①如图,S菱形ABCD=AB·DE,即菱形的面积等于底乘高;
② S菱形ABCD= AC·BD,即菱形的面积等于两条对角线乘积的一半.
A
B
C
D
E
O
应用举例
如图,四边形ABCD是边长为13 cm的菱形,其中对角线BD长10 cm.求:
(1)对角线AC的长度;
(2)菱形ABCD的面积.
【方法指导】(1)根据菱形的性质可得BD⊥AC,BE=DE= BD,然后利用勾股定理计算出AE的长,进而可得答案;
(2)将菱形分割成两个三角形或四个直角三角形,进而求出整个菱形的面积.
A
B
C
D
E
例1
解:(1)∵四边形ABCD是菱形,AC与BD相交于点E,
∴∠AED=90°(菱形的对角线互相垂直),
DE= BD= ×10=5(cm)(菱形的对角线互相平分),
∴AE= = =12(cm),
∴AC=2AE=2×12=24(cm)(菱形的对角线互相平分);
A
B
C
D
E
(2)菱形ABCD的面积
=△ABD的面积+△CBD的面积
=2×△ABD的面积
=2× ×BD×AE
=2× ×10×12
=120(cm2).
A
B
C
D
E
如图,在△ABC中,AB=BC,D,E,F分别是BC,AC,AB的中点.
(1)求证:四边形BDEF是菱形;
(2)AB=10 cm,求菱形BDEF的周长.
【方法指导】(1)根据三角形的中位线定理及菱形的定义可证出结论;
(2)根据中点的定义和菱形的四条边相等可得菱形BDEF的周长.
例2
A
B
C
D
E
F
解:(1)∵E,F分别是AC,AB的中点,
∴EF= BC,EF∥BC.
同理可证DE= AB,DE∥AB.
∴四边形BDEF是平行四边形.
∵AB=BC,∴EF=DE,
∴四边形BDEF是菱形;
A
B
C
D
E
F
(2)∵F是AB的中点,
∴BF= AB= ×10=5(cm),
∵四边形BDEF是菱形,
∴BD=DE=EF=BF,
∴菱形BDEF的周长为4×5=20(cm).
A
B
C
D
E
F
随堂练习
1.如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=2 cm,BD=4 cm,则菱形ABCD的面积是_____cm2.
4
8
2.如图,菱形ABCD的边长是4 cm,E是AB的中点,且DE⊥AB,则
S菱形ABCD=_____cm2.
D
A
C
B
O
A
D
C
B
E
第1题图
第2题图
3.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1∶2,周长是8 cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
A
B
C
D
O
解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AD∥BC.
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC= ×180°=60°,
∴∠ABO= ∠ABC=30°.
∵菱形ABCD的周长是8 cm,
A
B
C
D
O
∴AB=2 cm,
∴OA= AB=1(cm).
∴OB= = = (cm),
AC=2OA=2×1=2(cm).
∴BD=2OB=2 (cm);
(2)S菱形ABCD= AC·BD= ×2×2 =2 (cm2).
A
B
C
D
O
课堂小结
面积=底×高
=两条对角线乘积的一半
菱形的性质与判定的综合应用
菱形的面积
综合运用
北师大版 九年级上册
1.1 菱形的性质与判定
第3课时 菱形的性质与判定的综合应用
情景导入
我们已经研究了一个特殊的平行四边形——菱形,它的定义是什么呢?有哪些性质呢?
问题1:菱形的定义:___________________________________
问题2:菱形的性质:
(边)__________________________
(角)__________________________
(对角线)_______________________________________________
(对称性)_______________________________________________
有一组邻边相等的平行四边形叫做菱形
对边平行且四条边相等
对角相等,邻角互补
对角线互相垂直平分,并且每条对角线平分一组对角
既是轴对称图形,也是中心对称图形
实践探究
探究1
如图,两张等宽的纸条交叉重叠在一起,重叠部分ABCD是菱形吗?为什么?
A
B
C
D
证明:∵等宽纸条对边平行,
∴AD∥BC, AB∥CD,∴□ABCD 是平行四边形,
从 A点作AM⊥DC 交于点 M,
作AN⊥BC交于点 N,
∵是两张等宽的纸,∴AM = AN.
∵□ABCD 是平行四边形,∴∠ABN=∠ADM,
∵AM⊥DC ,AN⊥BC,∴∠ANB =∠AMD = 90°,
∴△ABN≌△ADM,∴AB = AD,
∴四边形 ABCD 是菱形(一组邻边相等的平行四边形是菱形)
探究2
若纸条的宽度是3,∠ABC=60°,你会求菱形的面积吗?你有几种不同的方法?
A
B
C
D
方法一:菱形是特殊的平行四边形,可以用“底×高”求菱形的面积.
解:过点A作AE⊥BC于点E,
在Rt△ABE中,∠B=60°,AE=3,
设BE=x(x>0),则AB=2x.
由勾股定理,得AB2=AE2+BE2,
即(2x)2=32+x2,解得x= ,
∴BE= ,AB=2 ,
S菱形ABCD=BC·AE=2 ×3=6 .
A
B
C
D
E
方法二:菱形的对角线互相垂直,可以用 AC·BD,求菱形的面积.
解:连接AC,BD交于点O,过点A作AE⊥BC于点E.
∵四边形ABCD为菱形,∠ABC=60°,
∴△ABC是等边三角形.
由方法(1)可知AB=2 ,
∴AB=BC=AC=2 ,
A
B
C
D
O
E
∴OA= .
在Rt△AOB中,由勾股定理,得
OB= = =3,
∴BD=2OB=2×3=6.
S菱形ABCD=2S△ABC= AC·OB×2= AC·BD= ×2 ×6=6 .
A
B
C
D
O
E
归纳总结
菱形面积的计算公式:
①如图,S菱形ABCD=AB·DE,即菱形的面积等于底乘高;
② S菱形ABCD= AC·BD,即菱形的面积等于两条对角线乘积的一半.
A
B
C
D
E
O
应用举例
如图,四边形ABCD是边长为13 cm的菱形,其中对角线BD长10 cm.求:
(1)对角线AC的长度;
(2)菱形ABCD的面积.
【方法指导】(1)根据菱形的性质可得BD⊥AC,BE=DE= BD,然后利用勾股定理计算出AE的长,进而可得答案;
(2)将菱形分割成两个三角形或四个直角三角形,进而求出整个菱形的面积.
A
B
C
D
E
例1
解:(1)∵四边形ABCD是菱形,AC与BD相交于点E,
∴∠AED=90°(菱形的对角线互相垂直),
DE= BD= ×10=5(cm)(菱形的对角线互相平分),
∴AE= = =12(cm),
∴AC=2AE=2×12=24(cm)(菱形的对角线互相平分);
A
B
C
D
E
(2)菱形ABCD的面积
=△ABD的面积+△CBD的面积
=2×△ABD的面积
=2× ×BD×AE
=2× ×10×12
=120(cm2).
A
B
C
D
E
如图,在△ABC中,AB=BC,D,E,F分别是BC,AC,AB的中点.
(1)求证:四边形BDEF是菱形;
(2)AB=10 cm,求菱形BDEF的周长.
【方法指导】(1)根据三角形的中位线定理及菱形的定义可证出结论;
(2)根据中点的定义和菱形的四条边相等可得菱形BDEF的周长.
例2
A
B
C
D
E
F
解:(1)∵E,F分别是AC,AB的中点,
∴EF= BC,EF∥BC.
同理可证DE= AB,DE∥AB.
∴四边形BDEF是平行四边形.
∵AB=BC,∴EF=DE,
∴四边形BDEF是菱形;
A
B
C
D
E
F
(2)∵F是AB的中点,
∴BF= AB= ×10=5(cm),
∵四边形BDEF是菱形,
∴BD=DE=EF=BF,
∴菱形BDEF的周长为4×5=20(cm).
A
B
C
D
E
F
随堂练习
1.如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=2 cm,BD=4 cm,则菱形ABCD的面积是_____cm2.
4
8
2.如图,菱形ABCD的边长是4 cm,E是AB的中点,且DE⊥AB,则
S菱形ABCD=_____cm2.
D
A
C
B
O
A
D
C
B
E
第1题图
第2题图
3.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1∶2,周长是8 cm.求:
(1)两条对角线的长度;
(2)菱形的面积.
A
B
C
D
O
解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AD∥BC.
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC= ×180°=60°,
∴∠ABO= ∠ABC=30°.
∵菱形ABCD的周长是8 cm,
A
B
C
D
O
∴AB=2 cm,
∴OA= AB=1(cm).
∴OB= = = (cm),
AC=2OA=2×1=2(cm).
∴BD=2OB=2 (cm);
(2)S菱形ABCD= AC·BD= ×2×2 =2 (cm2).
A
B
C
D
O
课堂小结
面积=底×高
=两条对角线乘积的一半
菱形的性质与判定的综合应用
菱形的面积
综合运用
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
