1.2.2 矩形的判定 课件(共25张PPT)
文档属性
| 名称 | 1.2.2 矩形的判定 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 07:52:31 | ||
图片预览





文档简介
(共25张PPT)
北师大版 九年级上册
1.2 矩形的性质与判定
第2课时 矩形的判定
情景导入
小华想做一个矩形相框送给妈妈做生日礼物,于是他用两根长度相等的短木条和两根长度相等的长木条制成矩形,你有什么办法可以验证他做的是矩形相框吗?
合作探究
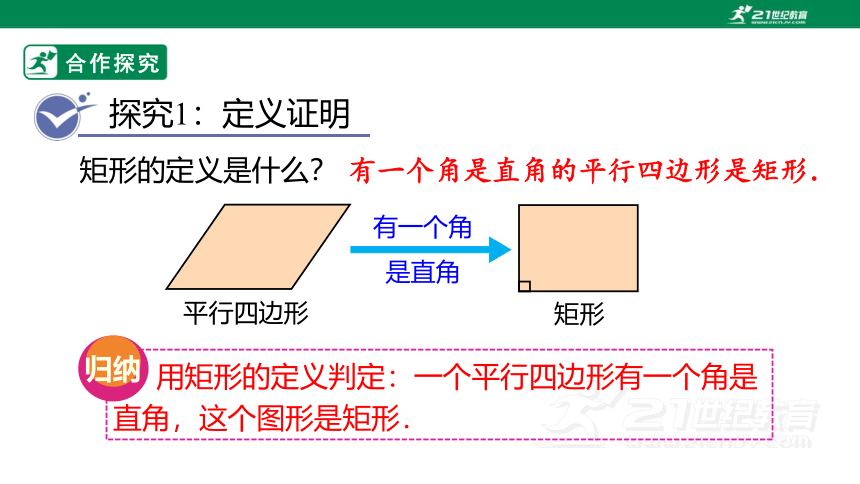
探究1:定义证明
矩形的定义是什么?
有一个角是直角的平行四边形是矩形.
有一个角
是直角
平行四边形
矩形
用矩形的定义判定:一个平行四边形有一个角是直角,这个图形是矩形.
归纳
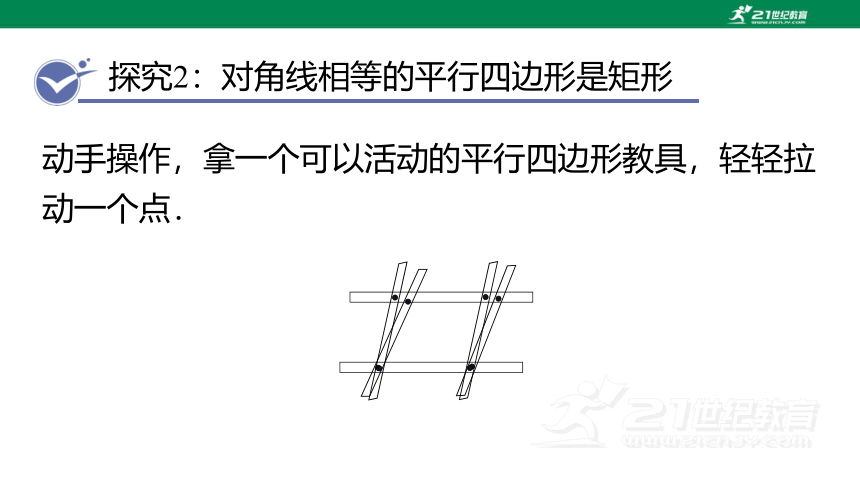
探究2:对角线相等的平行四边形是矩形
动手操作,拿一个可以活动的平行四边形教具,轻轻拉动一个点.
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
思考
答:随着∠α的增大,较长的对角线会变短,较短的对角线会变长.
α
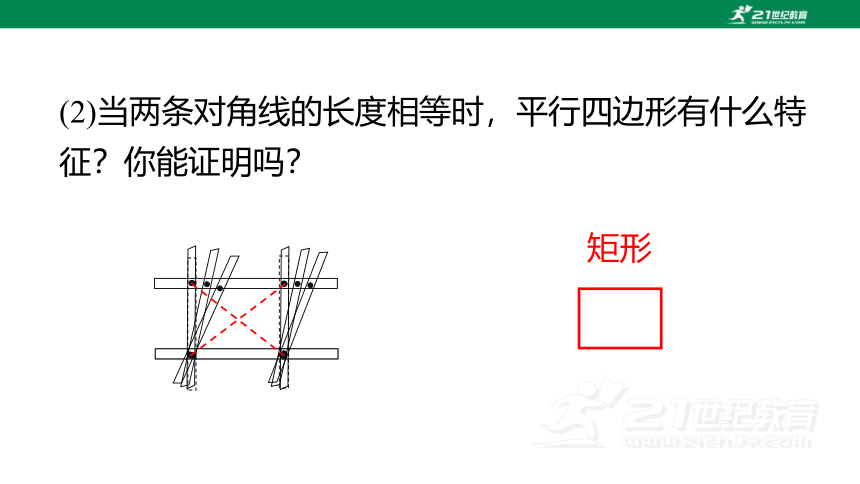
(2)当两条对角线的长度相等时,平行四边形有什么特征?你能证明吗?
矩形
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
证一证
已知:如图,在□ABCD中,对角线AC=BD.求证:平行四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形.
∴AB=CD, AB∥CD.
又∵AC=DB, BC=CB.
∴ △ABC≌△DCB.
∴∠ABC=∠DCB.
又∵AB∥CD.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=90°.
∴□ABCD是矩形.(矩形的定义).
D
B
C
A
归纳总结
矩形的判定1:
定理:对角线相等的平行四边形是矩形.
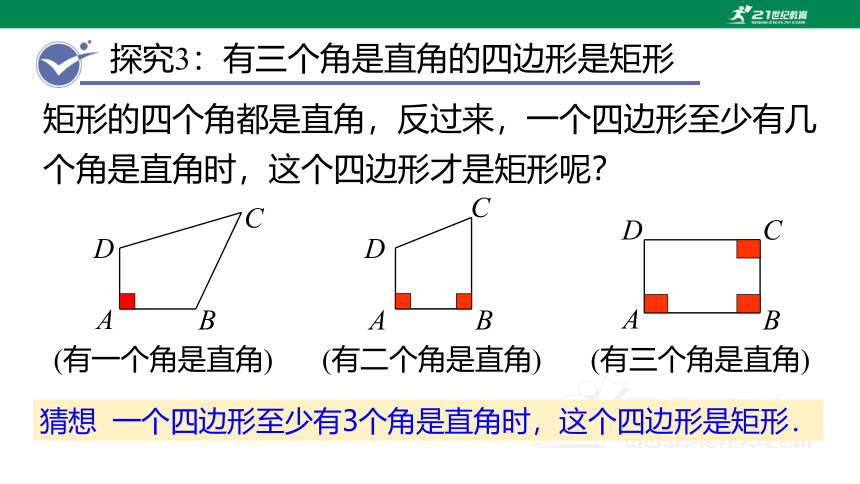
矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形才是矩形呢?
猜想 一个四边形至少有3个角是直角时,这个四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
探究3:有三个角是直角的四边形是矩形
证一证
分析:利用同旁内角互补,两直线平行来证明四边形是平行
四边形,可使问题得证.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC, AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
D
B
C
A
归纳总结
矩形的判定2:
定理:有三个角是直角的四边形是矩形.
应用举例
如图,在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4cm,求□ABCD的面积.
A
B
C
D
O
例1
【方法指导】先根据“对角线相等的平行四边形是矩形”判定□ABCD是矩形,再求出BC的长,从而可得□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD.
∵AO=BO,
∴□ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,AB=4cm,AC=2AO=8cm,
∴BC==4(cm).
∴S□ABCD=AB·BC=4×4=16(cm2).
A
B
C
D
O
如图,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,垂足分别为点E,D.
求证:四边形AEBD是矩形.
例2
【方法指导】根据角平分线的性质和平角的定义,得到∠EBD=90°,再结合AE⊥BE,AD⊥BD,可以确定四边形的三个内角都是直角,根据“有三个角是直角的四边形是矩形”就可以证明此四边形是矩形.
A
B
E
D
P
C
证明:∵BD,BE分别是∠ABC,∠ABP的平分线,
∴∠ABD+∠ABE= (∠ABC+∠ABP)=90°,
即∠EBD=90°.
又∵AE⊥BE,AD⊥BD,
∴∠AEB=∠ADB=90°,
∴四边形AEBD是矩形(有三个角都是直角的四边形是矩形).
A
B
E
D
P
C
证明:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH, 即EG=FH,
∴四边形EFGH是矩形.
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、
H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
例3
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD=∠BAC,∠CAN=∠CAM.
∴∠DAE=∠CAD+∠CAN= (∠BAC+
∠CAM)=×180°=90°.
在△ABC中,AB=AC,AD为∠BAC的平分线,
∴AD⊥BC,∴∠ADC=90°.
又∵CE⊥AN,∴∠CEA=90°.
∴四边形ADCE为矩形(有三个角是直角的四边形是矩形).
如图,在△ABC中,AB=AC,AD为∠BAC的平分线,
AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
例4
1. 下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有一个角是直角的四边形是矩形;( )
(5)有三个角是直角的四边形是矩形;( )
(6)四个角都相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形;( )
(4)有三个角都相等的四边形是矩形;( )
(8)一组对角互补的平行四边形是矩形.( )
练一练
×
×
×
×
√
√
√
√
随堂练习
1.下列说法正确的是 ( )
A.一组对边平行且相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
D
2.如图,□ABCD的对角线相交于点O,请你添加一个条件_________________________(只添加一个即可),使□ABCD是矩形.
AC=BD (答案不唯一)
3.如图,□ABCD的四个内角的平分线分别相交于E,F,G,H四点.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAB+∠ABC=180°.
∵□ABCD的四个内角平分线分别相交于E,F,G,H四点,由角平分线性质,得∠HAB= ∠DAB,∠ABH= ∠ABC,
∴∠HAB+∠ABH= (∠DAB+∠ABC)=90°,
∴∠H=90°.
同理可求得∠HEF=∠F=90°,
∴四边形EFGH是矩形.
A
B
C
D
H
E
D
G
4.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB.
∵AN=CM,ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,MN=BD,
∴平行四边形NDMB为矩形.
5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1) 经过多长时间,四边形PQCD是平行四边形?
解:设经过x s,四边形PQCD为平行四边形,
即PD=CQ,
所以24-x=3x,
解得x=6.
即经过6 s,四边形PQCD是平行四边形.
(2) 经过多长时间,四边形PQBA是矩形?
解:设经过y s,四边形PQBA为矩形,
即AP=BQ,
∴y=26-3y,
解得y=6.5,
即经过6.5 s,四边形PQBA是矩形.
课堂小结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
定义
判定定理
矩形的判定
北师大版 九年级上册
1.2 矩形的性质与判定
第2课时 矩形的判定
情景导入
小华想做一个矩形相框送给妈妈做生日礼物,于是他用两根长度相等的短木条和两根长度相等的长木条制成矩形,你有什么办法可以验证他做的是矩形相框吗?
合作探究
探究1:定义证明
矩形的定义是什么?
有一个角是直角的平行四边形是矩形.
有一个角
是直角
平行四边形
矩形
用矩形的定义判定:一个平行四边形有一个角是直角,这个图形是矩形.
归纳
探究2:对角线相等的平行四边形是矩形
动手操作,拿一个可以活动的平行四边形教具,轻轻拉动一个点.
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
思考
答:随着∠α的增大,较长的对角线会变短,较短的对角线会变长.
α
(2)当两条对角线的长度相等时,平行四边形有什么特征?你能证明吗?
矩形
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
证一证
已知:如图,在□ABCD中,对角线AC=BD.求证:平行四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形.
∴AB=CD, AB∥CD.
又∵AC=DB, BC=CB.
∴ △ABC≌△DCB.
∴∠ABC=∠DCB.
又∵AB∥CD.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=90°.
∴□ABCD是矩形.(矩形的定义).
D
B
C
A
归纳总结
矩形的判定1:
定理:对角线相等的平行四边形是矩形.
矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形才是矩形呢?
猜想 一个四边形至少有3个角是直角时,这个四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
探究3:有三个角是直角的四边形是矩形
证一证
分析:利用同旁内角互补,两直线平行来证明四边形是平行
四边形,可使问题得证.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC, AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
D
B
C
A
归纳总结
矩形的判定2:
定理:有三个角是直角的四边形是矩形.
应用举例
如图,在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4cm,求□ABCD的面积.
A
B
C
D
O
例1
【方法指导】先根据“对角线相等的平行四边形是矩形”判定□ABCD是矩形,再求出BC的长,从而可得□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD.
∵AO=BO,
∴□ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,AB=4cm,AC=2AO=8cm,
∴BC==4(cm).
∴S□ABCD=AB·BC=4×4=16(cm2).
A
B
C
D
O
如图,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,垂足分别为点E,D.
求证:四边形AEBD是矩形.
例2
【方法指导】根据角平分线的性质和平角的定义,得到∠EBD=90°,再结合AE⊥BE,AD⊥BD,可以确定四边形的三个内角都是直角,根据“有三个角是直角的四边形是矩形”就可以证明此四边形是矩形.
A
B
E
D
P
C
证明:∵BD,BE分别是∠ABC,∠ABP的平分线,
∴∠ABD+∠ABE= (∠ABC+∠ABP)=90°,
即∠EBD=90°.
又∵AE⊥BE,AD⊥BD,
∴∠AEB=∠ADB=90°,
∴四边形AEBD是矩形(有三个角都是直角的四边形是矩形).
A
B
E
D
P
C
证明:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH, 即EG=FH,
∴四边形EFGH是矩形.
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、
H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
例3
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD=∠BAC,∠CAN=∠CAM.
∴∠DAE=∠CAD+∠CAN= (∠BAC+
∠CAM)=×180°=90°.
在△ABC中,AB=AC,AD为∠BAC的平分线,
∴AD⊥BC,∴∠ADC=90°.
又∵CE⊥AN,∴∠CEA=90°.
∴四边形ADCE为矩形(有三个角是直角的四边形是矩形).
如图,在△ABC中,AB=AC,AD为∠BAC的平分线,
AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
例4
1. 下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有一个角是直角的四边形是矩形;( )
(5)有三个角是直角的四边形是矩形;( )
(6)四个角都相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形;( )
(4)有三个角都相等的四边形是矩形;( )
(8)一组对角互补的平行四边形是矩形.( )
练一练
×
×
×
×
√
√
√
√
随堂练习
1.下列说法正确的是 ( )
A.一组对边平行且相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
D
2.如图,□ABCD的对角线相交于点O,请你添加一个条件_________________________(只添加一个即可),使□ABCD是矩形.
AC=BD (答案不唯一)
3.如图,□ABCD的四个内角的平分线分别相交于E,F,G,H四点.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAB+∠ABC=180°.
∵□ABCD的四个内角平分线分别相交于E,F,G,H四点,由角平分线性质,得∠HAB= ∠DAB,∠ABH= ∠ABC,
∴∠HAB+∠ABH= (∠DAB+∠ABC)=90°,
∴∠H=90°.
同理可求得∠HEF=∠F=90°,
∴四边形EFGH是矩形.
A
B
C
D
H
E
D
G
4.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB.
∵AN=CM,ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,MN=BD,
∴平行四边形NDMB为矩形.
5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1) 经过多长时间,四边形PQCD是平行四边形?
解:设经过x s,四边形PQCD为平行四边形,
即PD=CQ,
所以24-x=3x,
解得x=6.
即经过6 s,四边形PQCD是平行四边形.
(2) 经过多长时间,四边形PQBA是矩形?
解:设经过y s,四边形PQBA为矩形,
即AP=BQ,
∴y=26-3y,
解得y=6.5,
即经过6.5 s,四边形PQBA是矩形.
课堂小结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
定义
判定定理
矩形的判定
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
