2.6.1 应用一元二次方程求解几何问题 课件(共22张PPT)
文档属性
| 名称 | 2.6.1 应用一元二次方程求解几何问题 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
北师大版 九年级上册
2.6 应用一元二次方程
第1课时 应用一元二次方程求几何问题
情景导入
回顾本章开始时梯子下滑的问题:
(1)在这个问题中,梯子顶端下滑1 m时,梯子底端滑动的距离大于1 m,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
(2)如果梯子的长度是13 m,梯子顶端与地面的垂直距离为12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
10 m
8 m
实践探究
探究1
问题1:怎样设未知数?
这个问题中存在什么样的等量关系?
如何用勾股定理列方程?
(1)设梯子顶端下滑x m时,梯子底端滑动的距离和它相等.
先求梯子底端原来离墙的距离:________________________.
等量关系是:梯子顶端现在离地的距离与梯子底端现在离墙的距离组成了直角三角形的两条________,斜边是____________,根据勾股定理可得:________________________________,解得_______________.
直角边
梯子的长度
(8-x)2+(6+x)2=102
x1=0,x2=2
探究2
x1=0是否符合题意?
∵x=0时,梯子没有下滑,
∴____________________________.
问题2:你能根据(1)的分析解答出(2)吗?
x=0不合题意,舍去,x=2
(2)解:梯子底端原来离墙的距离为
设梯子顶端下滑 x m时,梯子底端滑动的距离和它相等.
由题意,得 (12-x)2+(5+x)2=132,
解得 x1=0(不合题意,舍去),x2=7.
答:梯子顶端下滑7 m时,梯子底端滑动的距离和它相等.
列方程解应用题的步骤是:
①审;②设;③列;④解;⑤验;⑥答.
归纳
应用举例
例1
如图,某海军基地位于A处,在其正南方向200 n mile 处有一目标B,在B的正东方向200 n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
A
B
D
C
E
F
北
东
200
200
45°
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里,其中≈2.449 )
∵AD=CD BF=CF
解:连接DF,
∴DF是△ABC的中位线
∴ DF//AB且DF= AB
∵AB⊥BC AB=BC=200
∴DF⊥BC DF=100(海里)BF=100(海里)
A
B
D
C
E
F
北
东
200
200
45°
若设相遇时补给船的行程DE为x海里,
则相遇时军舰的行程应为AB+BE=2 x海里.
EF=AB+BF-(AB+BE) =(300-2 x)海里
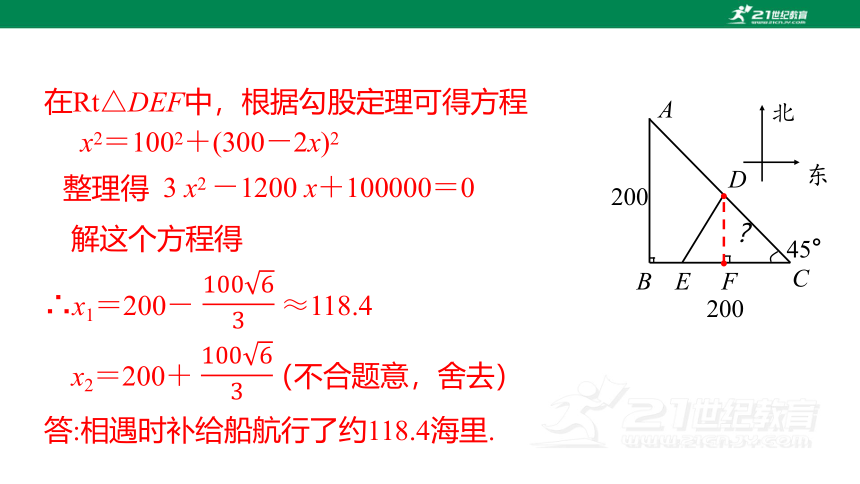
答:相遇时补给船航行了约118.4海里.
整理得
解这个方程得
在Rt△DEF中,根据勾股定理可得方程
x2=1002+(300-2x)2
3 x2 -1200 x+100000=0
∴x1=200- ≈118.4
x2=200+ (不合题意,舍去)
A
B
D
C
E
F
北
东
200
200
45°
例2
如图是长方形鸡场的平面示意图,一边靠墙,另外三边用竹篱笆围成,且竹篱笆总长为35 m.
(1)若所围的面积为150 m2,试求此长方形鸡场的长和宽;
(2)若墙长为18 m,则(1)中长方形鸡场的长和宽分别是多少?
(3)能围成面积为160 m2的长方形鸡场吗?说说你的理由.
A
B
C
D
方法指导:(1)若设BC=x m,则AB的长为 m,若设AB=x m,则BC=(35-2x) m,再利用题设中的等量关系,可求出(1)的解;
(2)墙长为18 m,意味着BC边的长应小于或等于18 m,从而对(1)的结论进行甄别即可;
(3)可借助(1)的解题思路构建方程,依据方程的根的情况可得结论.
A
B
C
D
解:(1)设BC=x m,则AB=CD= m.
依题意可列方程为x· =150,
整理,得x2-35x+300=0.
解这个方程,得x1=20,x2=15.
当BC=20 m时,AB=CD=7.5 m,
当BC=15 m时,AB=CD=10 m.
即这个长方形鸡场的长与宽分别为20 m,7.5 m或15 m,10 m;
A
B
C
D
(2)当墙长为18 m时,显然BC=20 m时,所围成的鸡场会在靠墙处留下一个缺口,不合题意,应舍去,此时所围成的长方形鸡场的长与宽只能是15 m,10 m;
A
B
C
D
(3)不能围成面积为160 m2的长方形鸡场.理由如下:
设BC=x m,则AB= m.
依题意可列方程为x· =160,
整理,得x2-35x+320=0.
此时Δ=352-4×1×320=1225-1280<0,
原方程没有实数根,
从而知用35 m的篱笆按图示方式不可能围成面积为160 m2的鸡场.
A
B
C
D
例3
在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路(两条纵向,一条横向,横向与纵向互相垂直)(如图1),把耕地分成大小相等的六块作试验田,要使试验田面积为570平方米,问道路应为多宽?
图(1)
解:设道路宽为x米,
如图(2)利用平移知识可列方程为
(32-2x)(20-x)=570,
化简得x2-36x+35=0,
解这个方程得x1=1,x2=35>32(不合题意,舍去),
∴道路宽应为1米.
图(2)
练一练
前年生产1吨乙种药品的成本是6000元.随着生产技术的进步,现在生产1吨乙种药品的成本是3600元,试求乙种药品成本的年平均下降率?
解:设乙种药品的年平均下降率为y.根据题意,列方程,得
6 000 ( 1-y )2 = 3 600.
解方程,得
y1≈0.225,y2≈1.775.
根据问题的实际意义,乙种药品成本的年平均下降率约为22.5%.
随堂练习
1.直角三角形的两条直角边的和为7,面积是6,则斜边长为 ( )
A. B.5 C. D.7
2.从正方形铁皮的一边切去一个2 cm宽的长方形,若余下的长方形面积是48 cm2,则原来正方形铁皮的面积是_________.
B
64 cm2
3.《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲乙行各几何。”
大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为 7,乙的速度为 3.乙一直向东走,甲先向南走了 10 步,后又斜向北偏东方向走了一段后与乙相遇。那么相遇时,甲、乙各走了多远?
解:设相遇时用的时间为x,
依题意可列方程为(3x)2=(7x-10)2-102,
整理,得2x2-7x=0.
解这个方程,得 x1=0(不合题意,舍去),
x2=3.5,
∴3x=3×3.5=10.5,7x=7×3.5=24.5.
答:相遇时,甲走了24.5步,乙走了10.5步.
4.用一根长40cm的铁丝围成一个面积为91cm2的矩形,问这个矩形长是多少?
解:设长为xcm,则宽为
解这个方程,得x1=7,x2=13.当x=7cm时,
当x=13cm时,
∴这个矩形的长为13cm.
5.一个直角三角形的斜边长为7cm,一条直角边比另一条直角边长1cm,那么这个直角三角形的面积是多少?
解:设较短直角边长为 x cm,由题意,得:
x2+(x+1)2=72,化简得:x2+x-24=0.
解这个方程得:
∴较长直角边长为
∴直角三角形面积=
课堂小结
列方程步骤:
应用类型
审
设
列
解
检
答
利用一元二次方程解决行程问题
行程问题
平均变化率问题
面积问题
动点问题
北师大版 九年级上册
2.6 应用一元二次方程
第1课时 应用一元二次方程求几何问题
情景导入
回顾本章开始时梯子下滑的问题:
(1)在这个问题中,梯子顶端下滑1 m时,梯子底端滑动的距离大于1 m,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
(2)如果梯子的长度是13 m,梯子顶端与地面的垂直距离为12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
10 m
8 m
实践探究
探究1
问题1:怎样设未知数?
这个问题中存在什么样的等量关系?
如何用勾股定理列方程?
(1)设梯子顶端下滑x m时,梯子底端滑动的距离和它相等.
先求梯子底端原来离墙的距离:________________________.
等量关系是:梯子顶端现在离地的距离与梯子底端现在离墙的距离组成了直角三角形的两条________,斜边是____________,根据勾股定理可得:________________________________,解得_______________.
直角边
梯子的长度
(8-x)2+(6+x)2=102
x1=0,x2=2
探究2
x1=0是否符合题意?
∵x=0时,梯子没有下滑,
∴____________________________.
问题2:你能根据(1)的分析解答出(2)吗?
x=0不合题意,舍去,x=2
(2)解:梯子底端原来离墙的距离为
设梯子顶端下滑 x m时,梯子底端滑动的距离和它相等.
由题意,得 (12-x)2+(5+x)2=132,
解得 x1=0(不合题意,舍去),x2=7.
答:梯子顶端下滑7 m时,梯子底端滑动的距离和它相等.
列方程解应用题的步骤是:
①审;②设;③列;④解;⑤验;⑥答.
归纳
应用举例
例1
如图,某海军基地位于A处,在其正南方向200 n mile 处有一目标B,在B的正东方向200 n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
A
B
D
C
E
F
北
东
200
200
45°
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里,其中≈2.449 )
∵AD=CD BF=CF
解:连接DF,
∴DF是△ABC的中位线
∴ DF//AB且DF= AB
∵AB⊥BC AB=BC=200
∴DF⊥BC DF=100(海里)BF=100(海里)
A
B
D
C
E
F
北
东
200
200
45°
若设相遇时补给船的行程DE为x海里,
则相遇时军舰的行程应为AB+BE=2 x海里.
EF=AB+BF-(AB+BE) =(300-2 x)海里
答:相遇时补给船航行了约118.4海里.
整理得
解这个方程得
在Rt△DEF中,根据勾股定理可得方程
x2=1002+(300-2x)2
3 x2 -1200 x+100000=0
∴x1=200- ≈118.4
x2=200+ (不合题意,舍去)
A
B
D
C
E
F
北
东
200
200
45°
例2
如图是长方形鸡场的平面示意图,一边靠墙,另外三边用竹篱笆围成,且竹篱笆总长为35 m.
(1)若所围的面积为150 m2,试求此长方形鸡场的长和宽;
(2)若墙长为18 m,则(1)中长方形鸡场的长和宽分别是多少?
(3)能围成面积为160 m2的长方形鸡场吗?说说你的理由.
A
B
C
D
方法指导:(1)若设BC=x m,则AB的长为 m,若设AB=x m,则BC=(35-2x) m,再利用题设中的等量关系,可求出(1)的解;
(2)墙长为18 m,意味着BC边的长应小于或等于18 m,从而对(1)的结论进行甄别即可;
(3)可借助(1)的解题思路构建方程,依据方程的根的情况可得结论.
A
B
C
D
解:(1)设BC=x m,则AB=CD= m.
依题意可列方程为x· =150,
整理,得x2-35x+300=0.
解这个方程,得x1=20,x2=15.
当BC=20 m时,AB=CD=7.5 m,
当BC=15 m时,AB=CD=10 m.
即这个长方形鸡场的长与宽分别为20 m,7.5 m或15 m,10 m;
A
B
C
D
(2)当墙长为18 m时,显然BC=20 m时,所围成的鸡场会在靠墙处留下一个缺口,不合题意,应舍去,此时所围成的长方形鸡场的长与宽只能是15 m,10 m;
A
B
C
D
(3)不能围成面积为160 m2的长方形鸡场.理由如下:
设BC=x m,则AB= m.
依题意可列方程为x· =160,
整理,得x2-35x+320=0.
此时Δ=352-4×1×320=1225-1280<0,
原方程没有实数根,
从而知用35 m的篱笆按图示方式不可能围成面积为160 m2的鸡场.
A
B
C
D
例3
在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路(两条纵向,一条横向,横向与纵向互相垂直)(如图1),把耕地分成大小相等的六块作试验田,要使试验田面积为570平方米,问道路应为多宽?
图(1)
解:设道路宽为x米,
如图(2)利用平移知识可列方程为
(32-2x)(20-x)=570,
化简得x2-36x+35=0,
解这个方程得x1=1,x2=35>32(不合题意,舍去),
∴道路宽应为1米.
图(2)
练一练
前年生产1吨乙种药品的成本是6000元.随着生产技术的进步,现在生产1吨乙种药品的成本是3600元,试求乙种药品成本的年平均下降率?
解:设乙种药品的年平均下降率为y.根据题意,列方程,得
6 000 ( 1-y )2 = 3 600.
解方程,得
y1≈0.225,y2≈1.775.
根据问题的实际意义,乙种药品成本的年平均下降率约为22.5%.
随堂练习
1.直角三角形的两条直角边的和为7,面积是6,则斜边长为 ( )
A. B.5 C. D.7
2.从正方形铁皮的一边切去一个2 cm宽的长方形,若余下的长方形面积是48 cm2,则原来正方形铁皮的面积是_________.
B
64 cm2
3.《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲乙行各几何。”
大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为 7,乙的速度为 3.乙一直向东走,甲先向南走了 10 步,后又斜向北偏东方向走了一段后与乙相遇。那么相遇时,甲、乙各走了多远?
解:设相遇时用的时间为x,
依题意可列方程为(3x)2=(7x-10)2-102,
整理,得2x2-7x=0.
解这个方程,得 x1=0(不合题意,舍去),
x2=3.5,
∴3x=3×3.5=10.5,7x=7×3.5=24.5.
答:相遇时,甲走了24.5步,乙走了10.5步.
4.用一根长40cm的铁丝围成一个面积为91cm2的矩形,问这个矩形长是多少?
解:设长为xcm,则宽为
解这个方程,得x1=7,x2=13.当x=7cm时,
当x=13cm时,
∴这个矩形的长为13cm.
5.一个直角三角形的斜边长为7cm,一条直角边比另一条直角边长1cm,那么这个直角三角形的面积是多少?
解:设较短直角边长为 x cm,由题意,得:
x2+(x+1)2=72,化简得:x2+x-24=0.
解这个方程得:
∴较长直角边长为
∴直角三角形面积=
课堂小结
列方程步骤:
应用类型
审
设
列
解
检
答
利用一元二次方程解决行程问题
行程问题
平均变化率问题
面积问题
动点问题
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
