3.1.2 利用概率判断游戏的公平性 课件(共26张PPT)
文档属性
| 名称 | 3.1.2 利用概率判断游戏的公平性 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 08:26:25 | ||
图片预览







文档简介
(共26张PPT)
北师大版 九年级上册
3.1 用树状图或表格求概率
第2课时 利用概率判断游戏的公平性
情景导入
“石头、剪刀、布”,又称“丁壳”,是一种流传多年的猜拳游戏,起源于中国,然后传猜到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近现代逐渐风靡世界.简单明了的法则,单次玩法比拼运气,多回合玩法比拼心理博弈,使得“石头、剪刀、布”这个古老的游戏同
时拥有“意外”与“技术”两种特性,深受
世界人民喜爱.那么同学们想一想“石
头、剪刀、布”有没有规则漏洞可钻呢?
实践探究
小可、子宣、欣怡三人在一起做游戏时,需要确定做游戏的先后顺序,她们约定用“石头、剪刀、布”的方式确定,那么在一个回合中,三个人都出“剪刀”的概率是多少?
问题1:这个游戏是几步试验完成?
问题2:每种都有几个可能性?
问题3:一共有多少种可能性?
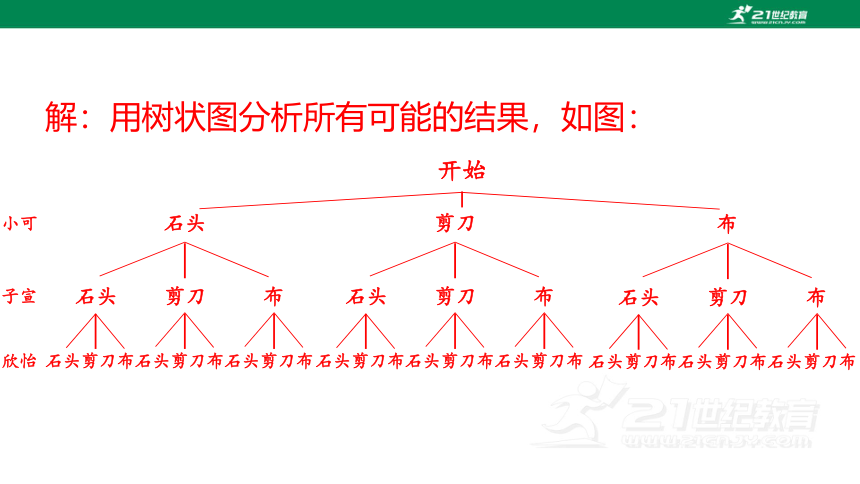
解:用树状图分析所有可能的结果,如图:
小可
子宣
开始
石头
剪刀
欣怡
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
剪刀
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
布
总共有27种可能的结果,每种结果出现的可能性相同,其中,三个人都出“剪刀”的结果只有1种,所以其概率为 .
当一次试验涉及更多的因素时,可采用树状图法把所有可能的结果都列出来.
归纳
应用举例
小明、小颖和小凡三人做 “石头、剪刀、布”游戏。游戏规则如下:
由小明和小颖做“石头” “剪刀”“布”的游戏,如果两人的手势相同,那么小凡获胜,如果两人手势不同那么按照“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 的规则决定 小明和小颖中的获胜者。
例1
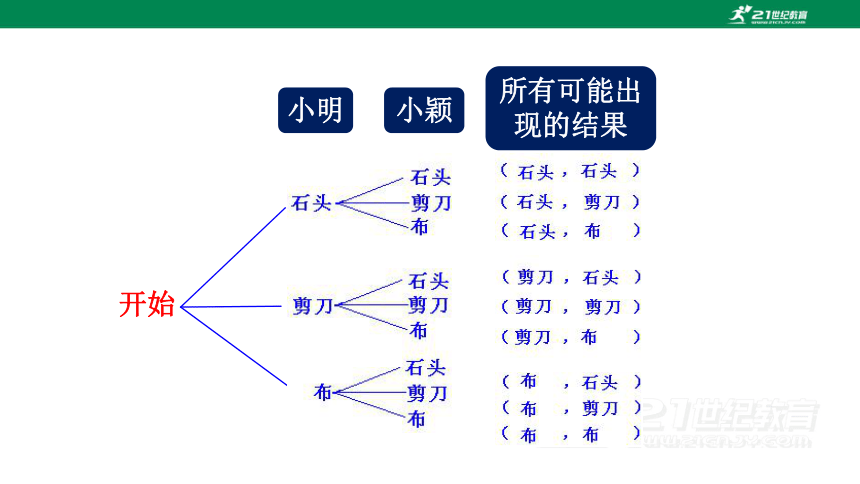
解:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
思考
小明
小颖
所有可能出现的结果
开始
共有九种可能的结果,每种结果出现的可能性相同,其中:
两人手势相同的有三种(石头,石头)(剪刀,剪刀)(布,布)所以小凡获胜的概率为
小明胜小颖的结果有三种(石头,剪刀)(剪刀,布)(布,石头)所以小明获胜的概率为
小颖胜小明的结果也有三种(剪刀,石头)(布,剪刀)(石头,布)所以小颖获胜的概率为
因此这个游戏对三人是公平的.
你能用列举的方法来解答吗?
小明和小军两人一起做游戏,游戏规则如下:
每人从1,2,…,12中任意选择一个数,然后两人各掷一次质地均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负,如果你是游戏者,你会选择哪个数?
例2
方法指导:这个问题看上去复杂,实际上等同于每人各掷一次质地均匀的骰子,将两人掷得的点数相加,看点数之和为几的概率最大.所以掷得的点数之和是哪个数的概率大,选择这个数后获胜的概率就大.理解到这一点之后学生通过列表法完成本题.
解:列表如下:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
总共有36种可能的结果,每种结果出现的可能性相同.其中,和为7的结果最多,有6种,其概率为 = ,所以如果我是游戏者,我会选择数字7.
第二个骰子
第一个骰子
同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
例3
1 2 3 4 5 6
1
2
3
4
5
6
第2枚
骰子
第1枚骰子
结
果
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
归纳总结
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
例4
解:利用表格列出所有可能的结果:
白 红1 红2
白
红1
红2
第一次
结果
第二次
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白 红1 红2
白
红1
红2
第一次
结果
第二次
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
什么时候用“列表法”方便,什么时候用“树形图”方便?
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法.
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图.
归纳总结
随堂练习
1.一个不透明的布袋中装有分别标有数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为 ( )
A. B. C. D.
B
2.一只昆虫在如图所示的树枝上爬行,假定昆虫在每个岔路口都会随机地选择一条路径,则它停留在A
叶面的概率是_____.
3.某市初中毕业男生体育测试项目有四项,其中“立定跳远” “1 000 m跑”“肺活量测试”为必测项目,另一项从“引体向上”或“推铅球”中选一项测试.小亮、小明和大刚从“引体向上”或“推
铅球”中选择同一个测试项目的概率是_____.
4.甲、乙、丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
解:画树状图如下:
第一个
第二个
开始
甲
乙
第三个
丙
乙
丙
甲
丙
甲
乙
丙
乙
丙
甲
乙
甲
总共有6种可能的结果,每种结果出现的可能性相同.
(1)由树状图可知,甲第一个出场的结果有2种:(甲、乙、丙)(甲、丙、乙),所以P(甲第一个出场)= = ;
(2)由树状图可知,甲比乙先出场的结果有3种:(甲、乙、丙)(甲、丙、乙)(丙、甲、乙),所以P(甲比乙先出场)=
= .
5.小明每天骑自行车上学都要经过三个安装有红绿灯的路口,假如每个路口红灯和绿灯亮的时间相等,那么,小明从家随时出发去学校,他至少遇到一次红灯的概率是多少?不遇红灯的概率是多少?
解:A表示红灯,B表示绿灯,根据题意画出树状图,
如图所示:
他至少遇到一次红灯的概率是
不遇红灯的概率是
课堂小结
树状图
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
北师大版 九年级上册
3.1 用树状图或表格求概率
第2课时 利用概率判断游戏的公平性
情景导入
“石头、剪刀、布”,又称“丁壳”,是一种流传多年的猜拳游戏,起源于中国,然后传猜到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近现代逐渐风靡世界.简单明了的法则,单次玩法比拼运气,多回合玩法比拼心理博弈,使得“石头、剪刀、布”这个古老的游戏同
时拥有“意外”与“技术”两种特性,深受
世界人民喜爱.那么同学们想一想“石
头、剪刀、布”有没有规则漏洞可钻呢?
实践探究
小可、子宣、欣怡三人在一起做游戏时,需要确定做游戏的先后顺序,她们约定用“石头、剪刀、布”的方式确定,那么在一个回合中,三个人都出“剪刀”的概率是多少?
问题1:这个游戏是几步试验完成?
问题2:每种都有几个可能性?
问题3:一共有多少种可能性?
解:用树状图分析所有可能的结果,如图:
小可
子宣
开始
石头
剪刀
欣怡
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
剪刀
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
布
总共有27种可能的结果,每种结果出现的可能性相同,其中,三个人都出“剪刀”的结果只有1种,所以其概率为 .
当一次试验涉及更多的因素时,可采用树状图法把所有可能的结果都列出来.
归纳
应用举例
小明、小颖和小凡三人做 “石头、剪刀、布”游戏。游戏规则如下:
由小明和小颖做“石头” “剪刀”“布”的游戏,如果两人的手势相同,那么小凡获胜,如果两人手势不同那么按照“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 的规则决定 小明和小颖中的获胜者。
例1
解:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
思考
小明
小颖
所有可能出现的结果
开始
共有九种可能的结果,每种结果出现的可能性相同,其中:
两人手势相同的有三种(石头,石头)(剪刀,剪刀)(布,布)所以小凡获胜的概率为
小明胜小颖的结果有三种(石头,剪刀)(剪刀,布)(布,石头)所以小明获胜的概率为
小颖胜小明的结果也有三种(剪刀,石头)(布,剪刀)(石头,布)所以小颖获胜的概率为
因此这个游戏对三人是公平的.
你能用列举的方法来解答吗?
小明和小军两人一起做游戏,游戏规则如下:
每人从1,2,…,12中任意选择一个数,然后两人各掷一次质地均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负,如果你是游戏者,你会选择哪个数?
例2
方法指导:这个问题看上去复杂,实际上等同于每人各掷一次质地均匀的骰子,将两人掷得的点数相加,看点数之和为几的概率最大.所以掷得的点数之和是哪个数的概率大,选择这个数后获胜的概率就大.理解到这一点之后学生通过列表法完成本题.
解:列表如下:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
总共有36种可能的结果,每种结果出现的可能性相同.其中,和为7的结果最多,有6种,其概率为 = ,所以如果我是游戏者,我会选择数字7.
第二个骰子
第一个骰子
同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
例3
1 2 3 4 5 6
1
2
3
4
5
6
第2枚
骰子
第1枚骰子
结
果
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
归纳总结
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
例4
解:利用表格列出所有可能的结果:
白 红1 红2
白
红1
红2
第一次
结果
第二次
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白 红1 红2
白
红1
红2
第一次
结果
第二次
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
什么时候用“列表法”方便,什么时候用“树形图”方便?
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法.
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图.
归纳总结
随堂练习
1.一个不透明的布袋中装有分别标有数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为 ( )
A. B. C. D.
B
2.一只昆虫在如图所示的树枝上爬行,假定昆虫在每个岔路口都会随机地选择一条路径,则它停留在A
叶面的概率是_____.
3.某市初中毕业男生体育测试项目有四项,其中“立定跳远” “1 000 m跑”“肺活量测试”为必测项目,另一项从“引体向上”或“推铅球”中选一项测试.小亮、小明和大刚从“引体向上”或“推
铅球”中选择同一个测试项目的概率是_____.
4.甲、乙、丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
解:画树状图如下:
第一个
第二个
开始
甲
乙
第三个
丙
乙
丙
甲
丙
甲
乙
丙
乙
丙
甲
乙
甲
总共有6种可能的结果,每种结果出现的可能性相同.
(1)由树状图可知,甲第一个出场的结果有2种:(甲、乙、丙)(甲、丙、乙),所以P(甲第一个出场)= = ;
(2)由树状图可知,甲比乙先出场的结果有3种:(甲、乙、丙)(甲、丙、乙)(丙、甲、乙),所以P(甲比乙先出场)=
= .
5.小明每天骑自行车上学都要经过三个安装有红绿灯的路口,假如每个路口红灯和绿灯亮的时间相等,那么,小明从家随时出发去学校,他至少遇到一次红灯的概率是多少?不遇红灯的概率是多少?
解:A表示红灯,B表示绿灯,根据题意画出树状图,
如图所示:
他至少遇到一次红灯的概率是
不遇红灯的概率是
课堂小结
树状图
步骤
用法
是一种解决试验有多步(或涉及多个因素)的好方法.
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果;
利用概率公式进行计算.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
