3.1.3 利用概率玩“配紫色”游戏 课件(共26张PPT)
文档属性
| 名称 | 3.1.3 利用概率玩“配紫色”游戏 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 08:29:42 | ||
图片预览






文档简介
(共26张PPT)
北师大版 九年级上册
3.1 用树状图或表格求概率
第3课时 利用概率玩“配紫色”游戏
情景导入
A盘
B盘
“配紫色”游戏:
小颖为学校联欢会设计一个“配紫色”游戏:
如下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘 A 转出红色,转盘 B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
红
白
蓝
黄
绿
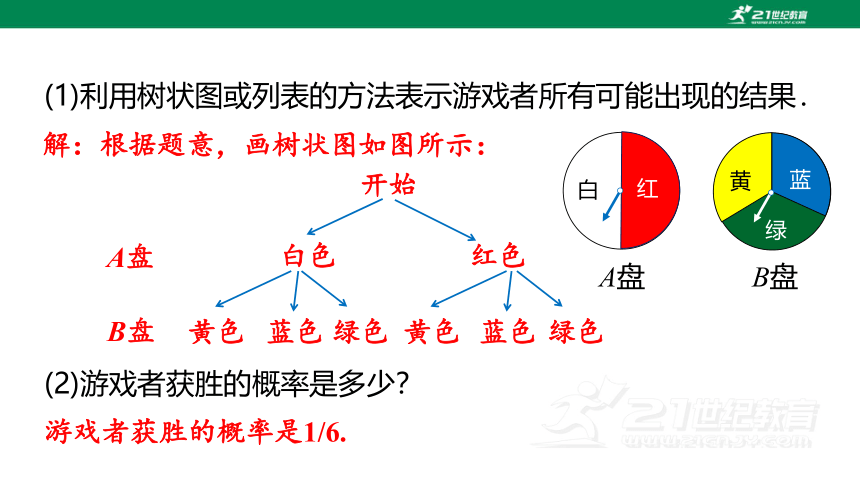
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
解:根据题意,画树状图如图所示:
开始
白色
红色
黄色
绿色
A盘
B盘
蓝色
黄色
绿色
蓝色
游戏者获胜的概率是1/6.
A盘
B盘
红
白
蓝
黄
绿
(2)游戏者获胜的概率是多少?
黄色 蓝色 绿色
白色 (白,黄) (白,蓝) (白,绿)
红色 (红,黄) (红,蓝) (红,绿)
B盘
A盘
表格如下:
游戏者获胜的概率是 .
A盘
B盘
红
白
蓝
黄
绿
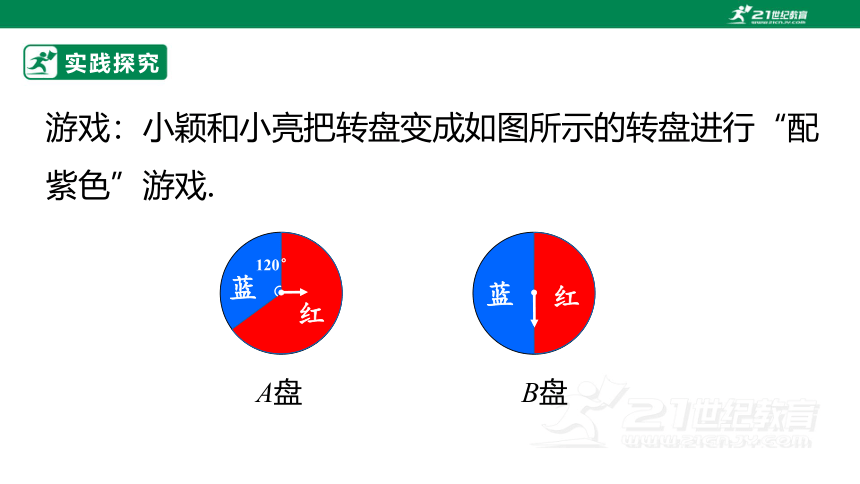
实践探究
游戏:小颖和小亮把转盘变成如图所示的转盘进行“配紫色”游戏.
A盘
B盘
蓝
120°
红
蓝
红
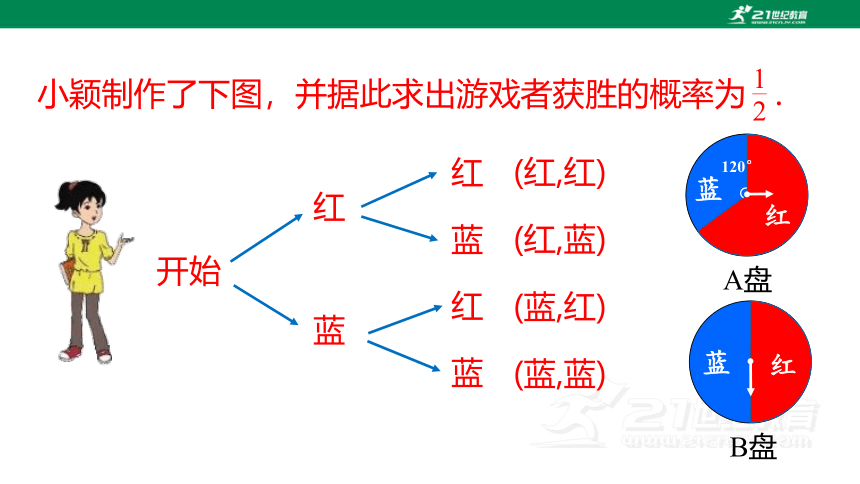
小颖制作了下图,并据此求出游戏者获胜的概率为 .
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
A盘
B盘
蓝
120°
红
蓝
红
小亮则先把转盘A的红色区域等分成2份,分别记作“红色1”“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是 .
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁做的对 说说你的理由.
蓝
120°
红1
红2
B盘
A盘
利用画树状图和列表的方法求概率时应注意些什么?
问题2
问题1
你认为谁做得对?说说你的理由.
小亮做得对,因为左边转盘中,红、蓝区域面积不相等,且红色区域的面积是蓝色区域面积的2倍,因此把红色区域2等分,这样出现的可能性才是相同的.
各种结果出现的可能性务必相同.
归纳总结
在试验中,包含的几种结果发生的可能性不等时,先通过转化为等可能实验,再利用画树状图或列表的方法求概率.
应用举例
例1
一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其他都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球.求两次摸到的球的颜色能配成紫色的概率.
1
1
2
2
方法指导:两个红球记作“红1”“红2”,两个白球记作“白1”“白2”,先用列表法把所有可能的结果表示出来,最后计算出配紫色的概率.
红1 红2 白1 白2 蓝
红1 (红1,红1) (红1,红2) (红1,白1) (红1,白2) (红1,蓝)
红2 (红2,红1) (红2,红2) (红2,白1) (红2,白2) (红2,蓝)
白1 (白1,红1) (白1,红2) (白1,白1) (白1,白2) (白1,蓝)
白2 (白2,红1) (白2,红2) (白2,白1) (白2,白2) (白2,蓝)
蓝 (蓝,红1) (蓝,红2) (蓝,白1) (蓝,白2) (蓝,蓝)
总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种.(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以
用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
例2
白
蓝
红
A盘
120°
红
蓝
B盘
方法指导:由图可知,转动A转盘时会出现三种可能的结果,但转出红色的可能性大些;转动B转盘时会出现两种可能的结果,但转出蓝色的可能性大些.由于这几种结果发生的可能性不等,所以不能直接用树状图或列
白
蓝
红
A盘
120°
红
蓝
B盘
表法表示试验出现的所有可能结果,而是要先将其转化.由图可知A转盘中红色区域是白色或蓝色的2倍,因此可将红色区域2等分.同理,可将B转盘中的蓝色区域2等分,从而将其转化为等可能性试验后,再用表格或树状图进行列举求解.
白
蓝
红1
A盘
红2
120°
红
蓝1
B盘
蓝2
解:将A转盘中“红”区域2等分,将B转盘中“蓝”区域2等分,如图:
白
蓝
红1
A盘
红2
120°
红
蓝1
B盘
蓝2
白 蓝 红1 红2
红 (白,红) (蓝,红) (红1,红) (红2,红)
蓝1 (白,蓝1) (蓝,蓝1) (红1,蓝1) (红2,蓝1)
蓝2 (白,蓝2) (蓝,蓝2) (红1,蓝2) (红2,蓝2)
总共有12种可能的结果,每种结果出现的可能性相同,其中能配得紫色的结果有5种:(蓝,红),(红1,蓝1),(红2,蓝1),
(红1,蓝2),(红2,蓝2),所以P(配得紫色)= .
A盘
B盘
例3
王铮擅长球类运动,课外活动时,足球队、篮球队都力邀他到自己的阵营,王铮左右为难,最后决定通过掷硬币来确定.游戏规则如下:连续抛掷硬币三次,如果两次正面朝上一次正面朝下,则王铮加入足球阵营;如果两次反面朝上,一次反面朝下,则王铮加入篮球阵营.
(1)用画树状图的方法表示三次抛
掷硬币的所有结果;
(2)这个游戏规则对两个球队是否
公平?为什么?
解:(1)根据题意画出树状图,如图.
开始
正
反
正
反
第一次
第二次
正
反
第三次
正
反
正
反
正
反
正
反
(2)这个游戏规则对两个球队公平.理由如下:
两次正面朝上一次正面朝下有3种结果:
正正反,正反正,反正正;
两次反面朝上一次反面朝下有3种结果:
正反反,反正反,反反正.
所以P(王铮去足球队)=P(王铮去篮球队)=
随堂练习
1.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么小李获胜的概率为 ( )
A. B. C. D.
A
2.用卡片进行有理数加法训练,李明手中的三张卡片分别是3、-1、-2,刘华手中的三张卡片分别是2、0、-1.如果每人随机抽取一张卡片,则和为正数的概率是 ( )
A. B. C. D.
D
3.甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打,规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打,若三人手势相同,则重新决定.那么通过一次
“手心手背”游戏能决定甲打乒乓球的概率是_____.
4.如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,配得紫色的概率是多少?
A盘
B盘
红
蓝
白
红
蓝
黄
配得紫色的概率为:
5.小颖设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,两个转盘停止转动时,若一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜.求游戏者获胜的概率.(指针指在分界线上则重转)
解:用表格来说明:
红色 蓝色
红1 (红1,红) (红1,蓝)
红2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
转盘1
转盘2
所以,配成紫色的概率
所以游戏者获胜的概率为 .
课堂小结
配紫色
判断游戏公平性
红色+蓝色=紫色
判断游戏参与者获
胜的概率是否相同
概率与游戏的综合应用
北师大版 九年级上册
3.1 用树状图或表格求概率
第3课时 利用概率玩“配紫色”游戏
情景导入
A盘
B盘
“配紫色”游戏:
小颖为学校联欢会设计一个“配紫色”游戏:
如下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘 A 转出红色,转盘 B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
红
白
蓝
黄
绿
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
解:根据题意,画树状图如图所示:
开始
白色
红色
黄色
绿色
A盘
B盘
蓝色
黄色
绿色
蓝色
游戏者获胜的概率是1/6.
A盘
B盘
红
白
蓝
黄
绿
(2)游戏者获胜的概率是多少?
黄色 蓝色 绿色
白色 (白,黄) (白,蓝) (白,绿)
红色 (红,黄) (红,蓝) (红,绿)
B盘
A盘
表格如下:
游戏者获胜的概率是 .
A盘
B盘
红
白
蓝
黄
绿
实践探究
游戏:小颖和小亮把转盘变成如图所示的转盘进行“配紫色”游戏.
A盘
B盘
蓝
120°
红
蓝
红
小颖制作了下图,并据此求出游戏者获胜的概率为 .
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
A盘
B盘
蓝
120°
红
蓝
红
小亮则先把转盘A的红色区域等分成2份,分别记作“红色1”“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是 .
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁做的对 说说你的理由.
蓝
120°
红1
红2
B盘
A盘
利用画树状图和列表的方法求概率时应注意些什么?
问题2
问题1
你认为谁做得对?说说你的理由.
小亮做得对,因为左边转盘中,红、蓝区域面积不相等,且红色区域的面积是蓝色区域面积的2倍,因此把红色区域2等分,这样出现的可能性才是相同的.
各种结果出现的可能性务必相同.
归纳总结
在试验中,包含的几种结果发生的可能性不等时,先通过转化为等可能实验,再利用画树状图或列表的方法求概率.
应用举例
例1
一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其他都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球.求两次摸到的球的颜色能配成紫色的概率.
1
1
2
2
方法指导:两个红球记作“红1”“红2”,两个白球记作“白1”“白2”,先用列表法把所有可能的结果表示出来,最后计算出配紫色的概率.
红1 红2 白1 白2 蓝
红1 (红1,红1) (红1,红2) (红1,白1) (红1,白2) (红1,蓝)
红2 (红2,红1) (红2,红2) (红2,白1) (红2,白2) (红2,蓝)
白1 (白1,红1) (白1,红2) (白1,白1) (白1,白2) (白1,蓝)
白2 (白2,红1) (白2,红2) (白2,白1) (白2,白2) (白2,蓝)
蓝 (蓝,红1) (蓝,红2) (蓝,白1) (蓝,白2) (蓝,蓝)
总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种.(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以
用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
例2
白
蓝
红
A盘
120°
红
蓝
B盘
方法指导:由图可知,转动A转盘时会出现三种可能的结果,但转出红色的可能性大些;转动B转盘时会出现两种可能的结果,但转出蓝色的可能性大些.由于这几种结果发生的可能性不等,所以不能直接用树状图或列
白
蓝
红
A盘
120°
红
蓝
B盘
表法表示试验出现的所有可能结果,而是要先将其转化.由图可知A转盘中红色区域是白色或蓝色的2倍,因此可将红色区域2等分.同理,可将B转盘中的蓝色区域2等分,从而将其转化为等可能性试验后,再用表格或树状图进行列举求解.
白
蓝
红1
A盘
红2
120°
红
蓝1
B盘
蓝2
解:将A转盘中“红”区域2等分,将B转盘中“蓝”区域2等分,如图:
白
蓝
红1
A盘
红2
120°
红
蓝1
B盘
蓝2
白 蓝 红1 红2
红 (白,红) (蓝,红) (红1,红) (红2,红)
蓝1 (白,蓝1) (蓝,蓝1) (红1,蓝1) (红2,蓝1)
蓝2 (白,蓝2) (蓝,蓝2) (红1,蓝2) (红2,蓝2)
总共有12种可能的结果,每种结果出现的可能性相同,其中能配得紫色的结果有5种:(蓝,红),(红1,蓝1),(红2,蓝1),
(红1,蓝2),(红2,蓝2),所以P(配得紫色)= .
A盘
B盘
例3
王铮擅长球类运动,课外活动时,足球队、篮球队都力邀他到自己的阵营,王铮左右为难,最后决定通过掷硬币来确定.游戏规则如下:连续抛掷硬币三次,如果两次正面朝上一次正面朝下,则王铮加入足球阵营;如果两次反面朝上,一次反面朝下,则王铮加入篮球阵营.
(1)用画树状图的方法表示三次抛
掷硬币的所有结果;
(2)这个游戏规则对两个球队是否
公平?为什么?
解:(1)根据题意画出树状图,如图.
开始
正
反
正
反
第一次
第二次
正
反
第三次
正
反
正
反
正
反
正
反
(2)这个游戏规则对两个球队公平.理由如下:
两次正面朝上一次正面朝下有3种结果:
正正反,正反正,反正正;
两次反面朝上一次反面朝下有3种结果:
正反反,反正反,反反正.
所以P(王铮去足球队)=P(王铮去篮球队)=
随堂练习
1.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么小李获胜的概率为 ( )
A. B. C. D.
A
2.用卡片进行有理数加法训练,李明手中的三张卡片分别是3、-1、-2,刘华手中的三张卡片分别是2、0、-1.如果每人随机抽取一张卡片,则和为正数的概率是 ( )
A. B. C. D.
D
3.甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打,规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打,若三人手势相同,则重新决定.那么通过一次
“手心手背”游戏能决定甲打乒乓球的概率是_____.
4.如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,配得紫色的概率是多少?
A盘
B盘
红
蓝
白
红
蓝
黄
配得紫色的概率为:
5.小颖设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,两个转盘停止转动时,若一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜.求游戏者获胜的概率.(指针指在分界线上则重转)
解:用表格来说明:
红色 蓝色
红1 (红1,红) (红1,蓝)
红2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
转盘1
转盘2
所以,配成紫色的概率
所以游戏者获胜的概率为 .
课堂小结
配紫色
判断游戏公平性
红色+蓝色=紫色
判断游戏参与者获
胜的概率是否相同
概率与游戏的综合应用
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
