3.1.1 用树状图或表格求随机事件的概率 课件(共28张PPT)
文档属性
| 名称 | 3.1.1 用树状图或表格求随机事件的概率 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 08:30:53 | ||
图片预览






文档简介
(共28张PPT)
北师大版 九年级上册
3.1 用树状图或表格求概率
第1课时 用树状图或表格求随机事件的概率
情景导入
1.抛掷一枚质地均匀的硬币,硬币落下后,会出现几种情况?分别是什么?每一种结果出现的可能性相同吗?
2.小明、小凡和小颖都想去看周末电影,但只有一张电影票.三人决定一起做游戏,谁获胜谁就去看电影.游戏规则如下:
小明
小颖
小凡
连续抛掷两枚均匀的硬币,如果两枚正面朝上,则小明获胜;如果两枚反面朝上,则小颖获胜;如果一枚正面朝上、一枚反面朝上,则小凡获胜.
你认为这个游戏公平吗?
实践探究
探究1
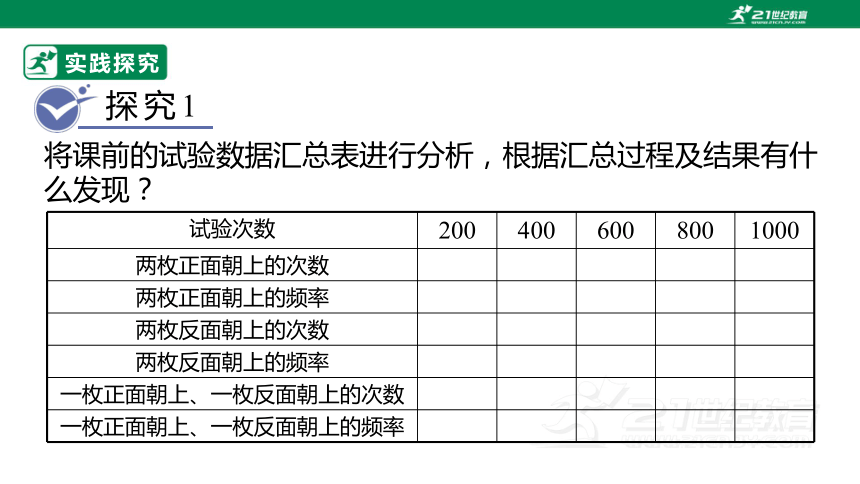
将课前的试验数据汇总表进行分析,根据汇总过程及结果有什么发现?
试验次数 200 400 600 800 1000
两枚正面朝上的次数
两枚正面朝上的频率
两枚反面朝上的次数
两枚反面朝上的频率
一枚正面朝上、一枚反面朝上的次数
一枚正面朝上、一枚反面朝上的频率
通过实验数据,你认为该游戏公平吗?
从上面的试验中我们发现,试验次数较大时,试验频率基本稳定,而且在一般情况下,“一枚正面朝上.一枚反面朝上”发生的概率大于其他两个事件发生的概率.所以,这个游戏不公平,它对小凡比较有利.
问题
在这个问题情境中,小明、小颖和小凡获得电影票的概率究竟是多大?请同学们思考如下问题:
(1)掷第一枚硬币可能出现哪些结果?它们发生的可能性是否一样?
(2)掷第二枚硬币可能出现哪些结果?它们发生的可能性是否一样?
(3)在第一枚硬币正面朝上的情况下,第二枚硬币可能出现哪些结
果?它们发生的可能性是否一样?如果第一枚硬币反面朝上呢?
探究2
由于硬币是均匀的,因此抛掷第一枚硬币出现“正面朝上”和“反面朝上”的概率相同.
无论抛掷第一枚硬币出现怎样的结果,抛掷第二枚硬币时出现“正面朝上”和“反面朝上”的概率也是相同的.
所以,抛掷两枚均匀的硬币,出现的(正,正)(正,反)(反,正)(反,反)四种情况是等可能的.
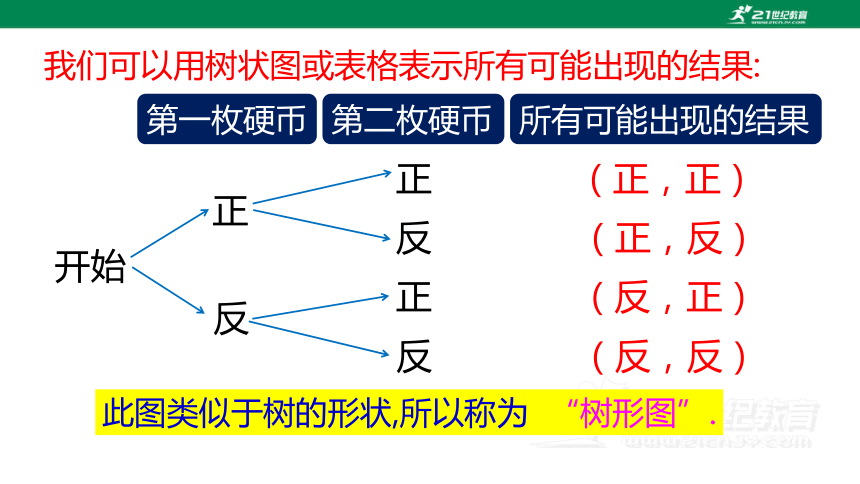
我们可以用树状图或表格表示所有可能出现的结果:
开始
正
正
第一枚硬币
反
(正,正)
(正,反)
反
正
反
(反,正)
(反,反)
第二枚硬币
所有可能出现的结果
此图类似于树的形状,所以称为 “树形图”.
用列表法列举所有可能出现的结果:
正 反
正
反
第二枚硬币
第一枚硬币
(正,正)
(正,反)
(反,正)
(反,反)
其中,小明获胜的结果有一种:(正,正).所以小明获胜的概率是 ;小颖获胜的结果有一种:(反,反).所以小颖获胜的概率也是 ;小凡获胜的结果有两种:(正,反)(反,正).所以小凡获胜的概率是 .因此,这个游戏对三人是不公平的.
归纳总结
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出某些事件发生的概率.
应用举例
小颖有两件上衣,分别为红色和白色,有两条裤子,分别为黑色和白色,她随机拿出一件上衣和一件裤子穿上,恰好是白色上衣和白色裤子的概率是多少?
例1
方法指导:可以用画树状图或列表法把所有情况列举出来.
解:解法1:画树状图如图所示:
总共有4种可能的结果,每种结果出现的可能性相同.其中恰好是白色上衣和白色裤子的结果有1种,所以其概率是 .
上衣:
裤子:
开始
红色
白色
黑色
白色
黑色
白色
裤子上衣 黑色 白色
红色 (红色,黑色) (红色,白色)
白色 (白色,黑色) (白色,白色)
解法2:列表如下:
总共有4种可能的结果,每种结果出现的可能性相同.其中,恰好是白色上衣和白色裤子的结果有1种,所以其概率是 .
在A、B两个盒子都装入写有数字0、1的两张卡片,分别从每个盒子里任取1张卡片,两张卡片上的数字之积为0的概率是多少?
例2
解法1:画树状图如下:
总共有4种可能的结果,每种结果出现的可能性相同,其中,两张卡片的数字之积为0的结果有3种,所以两张卡片上的数字之积为0的概率为 .
0 1
0
1
解法2:列表如下:
A
B
0
0
0
1
总共有4种可能的结果,每种结果出现的可能性相同.其中,两张卡片上的数字之积为0的结果有3种.所以两张卡片上的数字之积为0的概率为 .
把大小和形状一模一样的6张卡片分成两组,每组3张,分别标上数字1,2,3.将这两组卡片分别放入两个盒子中搅匀,再从中各随机抽取一张,试求取出的两张卡片数字之和为偶数的概率(要求用树状图或列表法求解).
练一练
解:画树状图:
由上图可知,所有等可能结果共有9种,其中两张卡片数字之和为偶数的结果有5种.
∴P(和为偶数)=
第一组
第二组
开始
1
2
3
1
2
3
1
2
3
1
2
3
列表如下:
1 2 3
1
2
3
第1组
第2组
由上图可知,所有等可能结果共有9种,其中两张卡片数字之和为偶数的结果有5种.
∴P(和为偶数)=
(1,1)
(1,2)
(1,3)
(2,1)
(2,2)
(2,3)
(3,1)
(3,2)
(3,3)
随堂练习
1.掷一枚质地均匀的硬币20次,下列说法正确的是 ( )
A.可能有10次正面朝上
B.必须10次正面朝上
C.掷2次必有1次正面朝上
D.不可能有20次正面朝上
A
2.小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是 ( )
A. B. C. D.
D
3.从两组牌面分别是1,2的牌中各摸一张牌,则其牌面数字之和为3的概率为_____.
4.小红上学经过两个十字路口,每个路口遇到红、绿灯的机会相同,小红希望上学时经过每个路口都是绿灯,出现这种情况的概率是_____.
5.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
(2)P(两车向右,一车向左)=
(3)P(至少两车向左)= .
(1)P(全部继续直行)=
27
7
6.现在学校决定由甲同学代表学校参加全县的诗歌朗诵比赛,甲同学有3件上衣,分别为红色(R)、黄色(Y)、蓝色(B),有2条裤子,分别为蓝色(B)和棕色(b)。甲同学想要穿蓝色上衣和蓝色裤子参加比赛,你知道甲同学任意拿出1件上衣和1条裤子,恰好是蓝色上衣和蓝色裤子的概率是多少吗?
上衣:
裤子:
解:用“树状图”列出所有可能出现的结果:
每种结果的出现是等可能的.“取出1件蓝色上衣和1条蓝色裤子”记为事件A ,那么事件A发生的概率是
P(A)=
所以,甲同学恰好穿上蓝色上衣和蓝色裤子的概率是
开始
上衣
裤子
所有可能出现的结果
课堂小结
列举法
关键
常用方法
直接列举法
列表法
画树状图法
两个试验因素或分两步进行的试验.
列表;
确定m、n值
代入概率公式计算.
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等.
基本步骤
适用对象
前提条件
北师大版 九年级上册
3.1 用树状图或表格求概率
第1课时 用树状图或表格求随机事件的概率
情景导入
1.抛掷一枚质地均匀的硬币,硬币落下后,会出现几种情况?分别是什么?每一种结果出现的可能性相同吗?
2.小明、小凡和小颖都想去看周末电影,但只有一张电影票.三人决定一起做游戏,谁获胜谁就去看电影.游戏规则如下:
小明
小颖
小凡
连续抛掷两枚均匀的硬币,如果两枚正面朝上,则小明获胜;如果两枚反面朝上,则小颖获胜;如果一枚正面朝上、一枚反面朝上,则小凡获胜.
你认为这个游戏公平吗?
实践探究
探究1
将课前的试验数据汇总表进行分析,根据汇总过程及结果有什么发现?
试验次数 200 400 600 800 1000
两枚正面朝上的次数
两枚正面朝上的频率
两枚反面朝上的次数
两枚反面朝上的频率
一枚正面朝上、一枚反面朝上的次数
一枚正面朝上、一枚反面朝上的频率
通过实验数据,你认为该游戏公平吗?
从上面的试验中我们发现,试验次数较大时,试验频率基本稳定,而且在一般情况下,“一枚正面朝上.一枚反面朝上”发生的概率大于其他两个事件发生的概率.所以,这个游戏不公平,它对小凡比较有利.
问题
在这个问题情境中,小明、小颖和小凡获得电影票的概率究竟是多大?请同学们思考如下问题:
(1)掷第一枚硬币可能出现哪些结果?它们发生的可能性是否一样?
(2)掷第二枚硬币可能出现哪些结果?它们发生的可能性是否一样?
(3)在第一枚硬币正面朝上的情况下,第二枚硬币可能出现哪些结
果?它们发生的可能性是否一样?如果第一枚硬币反面朝上呢?
探究2
由于硬币是均匀的,因此抛掷第一枚硬币出现“正面朝上”和“反面朝上”的概率相同.
无论抛掷第一枚硬币出现怎样的结果,抛掷第二枚硬币时出现“正面朝上”和“反面朝上”的概率也是相同的.
所以,抛掷两枚均匀的硬币,出现的(正,正)(正,反)(反,正)(反,反)四种情况是等可能的.
我们可以用树状图或表格表示所有可能出现的结果:
开始
正
正
第一枚硬币
反
(正,正)
(正,反)
反
正
反
(反,正)
(反,反)
第二枚硬币
所有可能出现的结果
此图类似于树的形状,所以称为 “树形图”.
用列表法列举所有可能出现的结果:
正 反
正
反
第二枚硬币
第一枚硬币
(正,正)
(正,反)
(反,正)
(反,反)
其中,小明获胜的结果有一种:(正,正).所以小明获胜的概率是 ;小颖获胜的结果有一种:(反,反).所以小颖获胜的概率也是 ;小凡获胜的结果有两种:(正,反)(反,正).所以小凡获胜的概率是 .因此,这个游戏对三人是不公平的.
归纳总结
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出某些事件发生的概率.
应用举例
小颖有两件上衣,分别为红色和白色,有两条裤子,分别为黑色和白色,她随机拿出一件上衣和一件裤子穿上,恰好是白色上衣和白色裤子的概率是多少?
例1
方法指导:可以用画树状图或列表法把所有情况列举出来.
解:解法1:画树状图如图所示:
总共有4种可能的结果,每种结果出现的可能性相同.其中恰好是白色上衣和白色裤子的结果有1种,所以其概率是 .
上衣:
裤子:
开始
红色
白色
黑色
白色
黑色
白色
裤子上衣 黑色 白色
红色 (红色,黑色) (红色,白色)
白色 (白色,黑色) (白色,白色)
解法2:列表如下:
总共有4种可能的结果,每种结果出现的可能性相同.其中,恰好是白色上衣和白色裤子的结果有1种,所以其概率是 .
在A、B两个盒子都装入写有数字0、1的两张卡片,分别从每个盒子里任取1张卡片,两张卡片上的数字之积为0的概率是多少?
例2
解法1:画树状图如下:
总共有4种可能的结果,每种结果出现的可能性相同,其中,两张卡片的数字之积为0的结果有3种,所以两张卡片上的数字之积为0的概率为 .
0 1
0
1
解法2:列表如下:
A
B
0
0
0
1
总共有4种可能的结果,每种结果出现的可能性相同.其中,两张卡片上的数字之积为0的结果有3种.所以两张卡片上的数字之积为0的概率为 .
把大小和形状一模一样的6张卡片分成两组,每组3张,分别标上数字1,2,3.将这两组卡片分别放入两个盒子中搅匀,再从中各随机抽取一张,试求取出的两张卡片数字之和为偶数的概率(要求用树状图或列表法求解).
练一练
解:画树状图:
由上图可知,所有等可能结果共有9种,其中两张卡片数字之和为偶数的结果有5种.
∴P(和为偶数)=
第一组
第二组
开始
1
2
3
1
2
3
1
2
3
1
2
3
列表如下:
1 2 3
1
2
3
第1组
第2组
由上图可知,所有等可能结果共有9种,其中两张卡片数字之和为偶数的结果有5种.
∴P(和为偶数)=
(1,1)
(1,2)
(1,3)
(2,1)
(2,2)
(2,3)
(3,1)
(3,2)
(3,3)
随堂练习
1.掷一枚质地均匀的硬币20次,下列说法正确的是 ( )
A.可能有10次正面朝上
B.必须10次正面朝上
C.掷2次必有1次正面朝上
D.不可能有20次正面朝上
A
2.小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是 ( )
A. B. C. D.
D
3.从两组牌面分别是1,2的牌中各摸一张牌,则其牌面数字之和为3的概率为_____.
4.小红上学经过两个十字路口,每个路口遇到红、绿灯的机会相同,小红希望上学时经过每个路口都是绿灯,出现这种情况的概率是_____.
5.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两车向右,一车向左;
(3)至少两车向左.
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
(2)P(两车向右,一车向左)=
(3)P(至少两车向左)= .
(1)P(全部继续直行)=
27
7
6.现在学校决定由甲同学代表学校参加全县的诗歌朗诵比赛,甲同学有3件上衣,分别为红色(R)、黄色(Y)、蓝色(B),有2条裤子,分别为蓝色(B)和棕色(b)。甲同学想要穿蓝色上衣和蓝色裤子参加比赛,你知道甲同学任意拿出1件上衣和1条裤子,恰好是蓝色上衣和蓝色裤子的概率是多少吗?
上衣:
裤子:
解:用“树状图”列出所有可能出现的结果:
每种结果的出现是等可能的.“取出1件蓝色上衣和1条蓝色裤子”记为事件A ,那么事件A发生的概率是
P(A)=
所以,甲同学恰好穿上蓝色上衣和蓝色裤子的概率是
开始
上衣
裤子
所有可能出现的结果
课堂小结
列举法
关键
常用方法
直接列举法
列表法
画树状图法
两个试验因素或分两步进行的试验.
列表;
确定m、n值
代入概率公式计算.
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等.
基本步骤
适用对象
前提条件
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
