4.4.4 黄金分割 课件(共22张PPT)
文档属性
| 名称 | 4.4.4 黄金分割 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
北师大版 九年级上册
4.4 探索三角形相似的条件
第4课时 黄金分割
情景导入
神奇的金字塔
美丽的大自然
迷人的芭蕾舞
现实生活中存在许多优美的图画和建筑,例如古埃及金字塔、大自然摄影、芭蕾舞,这些图形的边长之间的比都接近某一个数,你知道这个数是多少吗?
实践探究
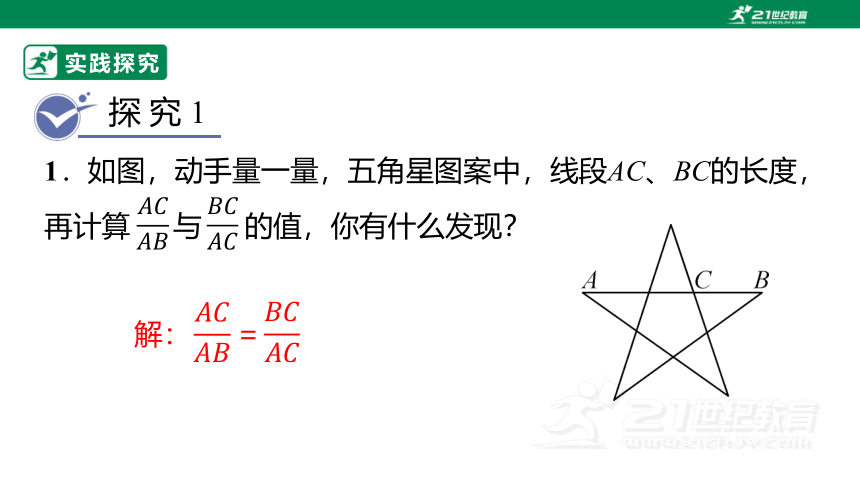
1.如图,动手量一量,五角星图案中,线段AC、BC的长度,再计算 与 的值,你有什么发现?
探究1
解: =
一般地,点C把线段AB分成两条线段AC和BC,如果
= ,那么称线段AB被点C黄金分割,点______叫做线段_______的黄金分割点,_______与_______的比叫做黄金比.
探究2
C
AB
AC
AB
探究3
一条线段有几个黄金分割点,黄金分割时,黄金比
= ,所以一条线段有_____个黄金分割点.
2
A
B
点1
点2
应用举例
例1
如图,计算黄金比.
解:由 = ,得AC2= AB·BC.
设AB = 1,AC = x,则BC = 1 – x.
∴ x2 = 1 ×(1 - x).
即 x2 + x – 1 = 0.
解方程得:x1= ,x2= (不合题意,舍去)
黄金比 = ≈ 0.618.
A
B
C
如何找到一条线段的黄金分割点?
已知线段AB,按照如下方法画图:
(1)过B作BD⊥AB使BD= AB;
(2)连接AD,在DA上截取DE=DB;
(3)在AB上截取AC=AE,则点C即为线段AB的黄金分割点.
提出问题:为什么点C为线段AB的黄金分割点?
例2
A
B
D
E
C
解:AB=2,则BD=DE= AB=1.
∴AD= = ,∴AC=AE=AD-DE= -1,
∴BC=AB-AC=2-( -1)=3- ,
∴AC2=( -1)2=6-2 ,AB·BC=2×(3- )=6-2 .
∴AC2=AB·BC,即 = .
∴点C是线段AB的黄金分割点.
A
B
D
E
C
在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
方法指导:想要看起来更美,则鞋底到肚脐的长度与身高之比应为黄金比,此题应根据已知条件求出肚脐到脚底的距离,再求高跟鞋的高度.
例3
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
练一练
1.已知点C是线段AB的黄金分割点,且AC>BC,则下列等式成立的是 ( )
A.AB2=AC·CB B.CB2=AC·AB
C.AC2=CB·AB D.AC2=2AB·BC
C
A
B
C
2.如图,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是 ( )
A
3.已知C是线段AB的一个黄金分割点,则AC : AB为( )
D
随堂练习
1.点C把线段AB分成两条线段AC和BC,如果 = ,那么下列说法错误的是 ( )
A.线段AB被点C黄金分割 B.点C叫做AB的黄金分割点
C.AC与AB的比叫做黄金比 D.AC= BC
2.小明同学发现自己一本书的宽与长的比为黄金比.已知这本书的长为10 cm,则它的宽约为 ( )
A.6.18 cm B.6.80 cm C.16.18 cm D.3.82 cm
D
A
3.如图,扇子的圆心角为α,余下扇形的圆心角为β,α与β的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则α=______.
4.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割,已知AB=10 cm,则AC的长约为______cm.(结果精确到0.1 cm)
135°
6.2
5.以长为2的线段AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到点F,使EF=EB.以线段AF为边作正方形AFGH,点H在AB上,如图所示.
(1)求线段AH,BH的长;
(2)求证:AH2=AB·BH;
(3)根据(2)中的结论,你能找出图中的
黄金分割点吗?
A
B
C
D
E
F
G
H
解:(1)E为AD的中点,∴AE=1.
在Rt△AEB中,由勾股定理,得BE2=AE2+AB2=12+22.
∴BE= ,∴EF=BE= .
∴AF= -1.
∵四边形AFGH是正方形,
∴AH=AF= -1,
∴BH=AB-AH=2-( -1)=3- ;
A
B
C
D
E
F
G
H
(2)AH2=( -1)2=6-2 ,
AB·BH=2×(3- )=6-2 ,
∴AH2=AB·BH;
(3)H是线段AB的黄金分割点.
A
B
C
D
E
F
G
H
6. 如图:在△ABC中,AB=AC, ∠BAC=36°, BD平分∠ABC交AC于点D, 求证:D是AC的黄金分割点.
证明:在等腰△ABC中,顶角∠A=36°,
所以∠ABC=∠C=72°,
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°,
在△ACB和△BCD中,∠BDC=72°
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD,
∴AC:BC=BC:DC;
∵∠A=∠ABD,
∴AD=BD.
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°,
∴BD=BC,
∴AD=BC,
∴AC:AD=AD:DC;
即点D是AC的黄金分割点.
课堂小结
北师大版 九年级上册
4.4 探索三角形相似的条件
第4课时 黄金分割
情景导入
神奇的金字塔
美丽的大自然
迷人的芭蕾舞
现实生活中存在许多优美的图画和建筑,例如古埃及金字塔、大自然摄影、芭蕾舞,这些图形的边长之间的比都接近某一个数,你知道这个数是多少吗?
实践探究
1.如图,动手量一量,五角星图案中,线段AC、BC的长度,再计算 与 的值,你有什么发现?
探究1
解: =
一般地,点C把线段AB分成两条线段AC和BC,如果
= ,那么称线段AB被点C黄金分割,点______叫做线段_______的黄金分割点,_______与_______的比叫做黄金比.
探究2
C
AB
AC
AB
探究3
一条线段有几个黄金分割点,黄金分割时,黄金比
= ,所以一条线段有_____个黄金分割点.
2
A
B
点1
点2
应用举例
例1
如图,计算黄金比.
解:由 = ,得AC2= AB·BC.
设AB = 1,AC = x,则BC = 1 – x.
∴ x2 = 1 ×(1 - x).
即 x2 + x – 1 = 0.
解方程得:x1= ,x2= (不合题意,舍去)
黄金比 = ≈ 0.618.
A
B
C
如何找到一条线段的黄金分割点?
已知线段AB,按照如下方法画图:
(1)过B作BD⊥AB使BD= AB;
(2)连接AD,在DA上截取DE=DB;
(3)在AB上截取AC=AE,则点C即为线段AB的黄金分割点.
提出问题:为什么点C为线段AB的黄金分割点?
例2
A
B
D
E
C
解:AB=2,则BD=DE= AB=1.
∴AD= = ,∴AC=AE=AD-DE= -1,
∴BC=AB-AC=2-( -1)=3- ,
∴AC2=( -1)2=6-2 ,AB·BC=2×(3- )=6-2 .
∴AC2=AB·BC,即 = .
∴点C是线段AB的黄金分割点.
A
B
D
E
C
在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
方法指导:想要看起来更美,则鞋底到肚脐的长度与身高之比应为黄金比,此题应根据已知条件求出肚脐到脚底的距离,再求高跟鞋的高度.
例3
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
练一练
1.已知点C是线段AB的黄金分割点,且AC>BC,则下列等式成立的是 ( )
A.AB2=AC·CB B.CB2=AC·AB
C.AC2=CB·AB D.AC2=2AB·BC
C
A
B
C
2.如图,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是 ( )
A
3.已知C是线段AB的一个黄金分割点,则AC : AB为( )
D
随堂练习
1.点C把线段AB分成两条线段AC和BC,如果 = ,那么下列说法错误的是 ( )
A.线段AB被点C黄金分割 B.点C叫做AB的黄金分割点
C.AC与AB的比叫做黄金比 D.AC= BC
2.小明同学发现自己一本书的宽与长的比为黄金比.已知这本书的长为10 cm,则它的宽约为 ( )
A.6.18 cm B.6.80 cm C.16.18 cm D.3.82 cm
D
A
3.如图,扇子的圆心角为α,余下扇形的圆心角为β,α与β的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则α=______.
4.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割,已知AB=10 cm,则AC的长约为______cm.(结果精确到0.1 cm)
135°
6.2
5.以长为2的线段AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到点F,使EF=EB.以线段AF为边作正方形AFGH,点H在AB上,如图所示.
(1)求线段AH,BH的长;
(2)求证:AH2=AB·BH;
(3)根据(2)中的结论,你能找出图中的
黄金分割点吗?
A
B
C
D
E
F
G
H
解:(1)E为AD的中点,∴AE=1.
在Rt△AEB中,由勾股定理,得BE2=AE2+AB2=12+22.
∴BE= ,∴EF=BE= .
∴AF= -1.
∵四边形AFGH是正方形,
∴AH=AF= -1,
∴BH=AB-AH=2-( -1)=3- ;
A
B
C
D
E
F
G
H
(2)AH2=( -1)2=6-2 ,
AB·BH=2×(3- )=6-2 ,
∴AH2=AB·BH;
(3)H是线段AB的黄金分割点.
A
B
C
D
E
F
G
H
6. 如图:在△ABC中,AB=AC, ∠BAC=36°, BD平分∠ABC交AC于点D, 求证:D是AC的黄金分割点.
证明:在等腰△ABC中,顶角∠A=36°,
所以∠ABC=∠C=72°,
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°,
在△ACB和△BCD中,∠BDC=72°
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD,
∴AC:BC=BC:DC;
∵∠A=∠ABD,
∴AD=BD.
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°,
∴BD=BC,
∴AD=BC,
∴AC:AD=AD:DC;
即点D是AC的黄金分割点.
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
