4.7.1 相似三角形中的对应线段之比 课件(共23张PPT)
文档属性
| 名称 | 4.7.1 相似三角形中的对应线段之比 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 08:50:42 | ||
图片预览





文档简介
(共23张PPT)
北师大版 九年级上册
4.7 相似三角形的性质
第1课时 相似三角形中的对应线段之比
情景导入
1.什么叫相似三角形?相似比指的是什么?
2.全等三角形是相似三角形吗?全等三角形的相似比是什么?
3.相似三角形的判定方法有哪些?
4.根据相似三角形的概念可知相似三角形有哪些性质?
5.相似三角形还有其他的性质吗?
实践探究
探究1
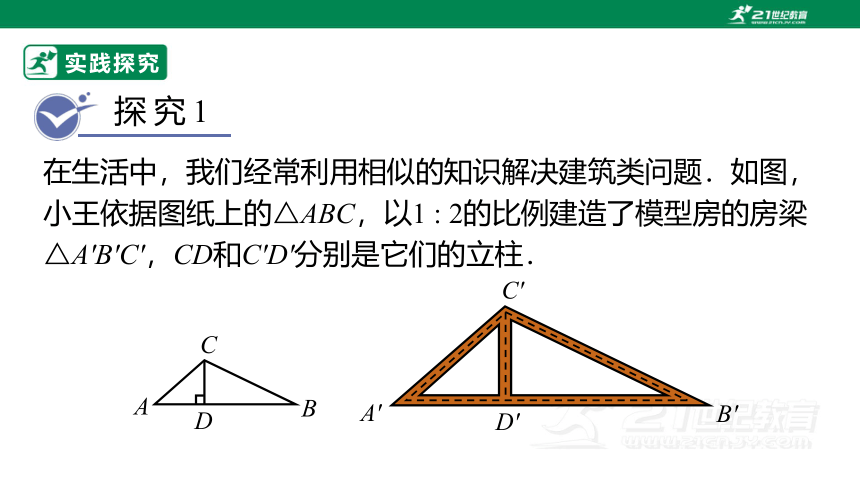
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1 : 2的比例建造了模型房的房梁△A′B′C′,CD和C′D′分别是它们的立柱.
A
B
C
D
A′
B′
C′
D′
思考
问题1:试写出△ABC与△A′B′C′的对应边之间的关系和对应角之间的关系.
问题2:△ACD与△A′C′D′相似吗?为什么?如果相似,指出它们的相似比.
A
B
C
D
A′
B′
C′
D′
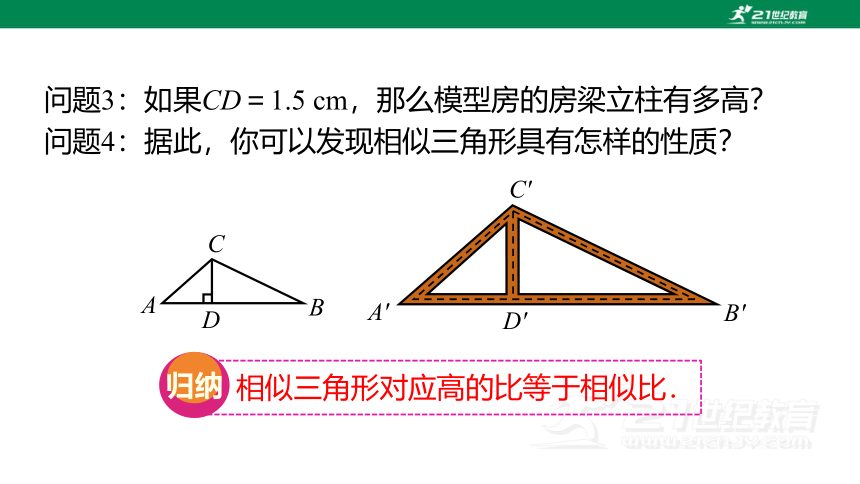
问题3:如果CD=1.5 cm,那么模型房的房梁立柱有多高?
问题4:据此,你可以发现相似三角形具有怎样的性质?
相似三角形对应高的比等于相似比.
归纳
A
B
C
D
A′
B′
C′
D′
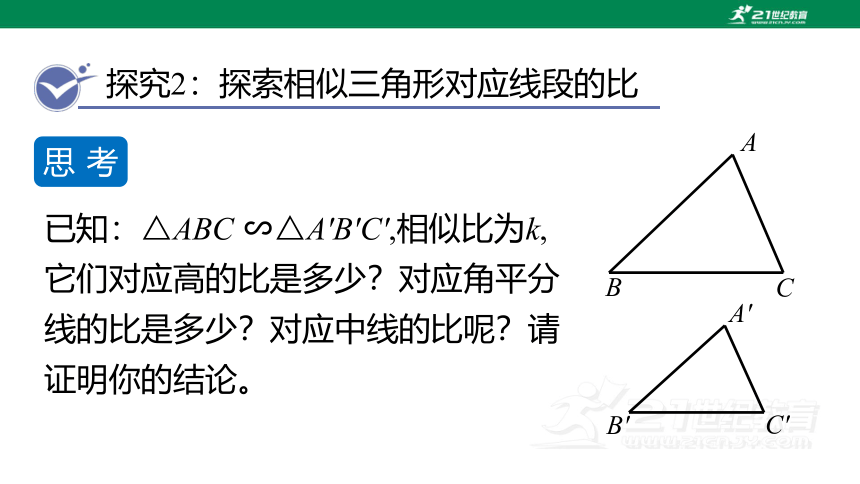
探究2:探索相似三角形对应线段的比
思考
已知:△ABC ∽△A′B′C′,相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?请证明你的结论。
A
B
C
A′
B′
C′
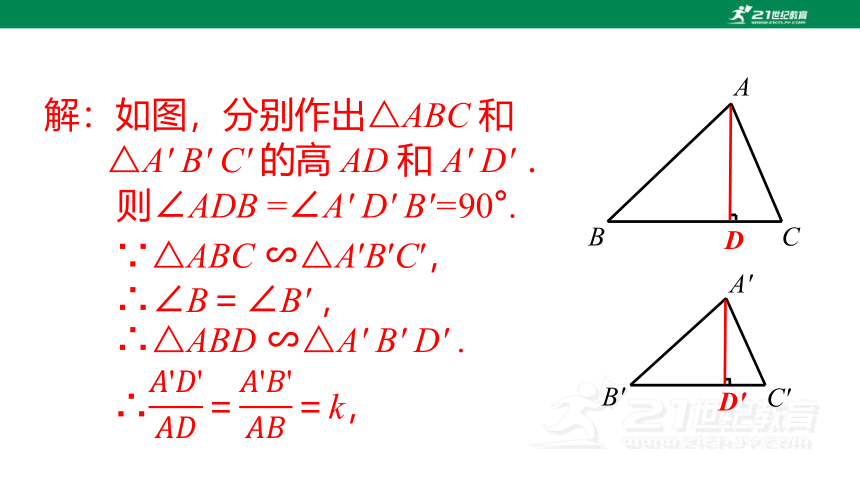
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出△ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A′
B′
C′
D
D′
∴ = =k,
A
B
C
F
A′
B′
C′
F′
A
B
C
E
A′
B′
C′
E′
相似三角形对应角的角平分线之比等于相似比.
相似三角形对应边上的中线比等于相似比.
归纳总结
1.相似三角形对应边的比等于________.
2.相似三角形的各对应角_______,各对应边_________.
3.相似三角形对应高的比、对应__________的比、对应________的比都等于相似比.
相似比
相等
成比例
角平分线
中线
应用举例
例1
如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR= BC时,求DE的长.如果SR= BC呢?
方法指导:相似三角形的判定及相似三角形的性质.
B
A
E
R
C
D
S
解:∵SR⊥AD,BC⊥AD,
∴SR∥BC.
∴∠ASR=∠B,∠ARS=∠C.
(相似三角形对应高的比等于相似比),
∴△ASR∽△ABC
(两角分别相等的两个三角形相似).
B
A
E
R
C
D
S
B
A
E
R
C
D
S
如图,CD是Rt△ABC 的斜边AB上的高.
(1)则图中有几对相似三角形?
(2)若AD=9 cm,CD=6 cm,求BD;
(3)若AB=25 cm,BC=15 cm,求BD.
方法指导:相似三角形的判定和性质的综合应用.
例2
A
B
C
D
解:(1)∵CD⊥AB,
∴∠ADC=∠BDC=∠ACB=90°.
在△ADC和△ACB中,∠ADC=∠ACB=90°,∠A=∠A,∴△ADC∽△ACB,
同理可知,△CDB∽△ACB,△ADC∽△CDB.
所以图中有三对相似三角形;
A
B
C
D
(2)∵△ACD∽△CBD,
∴ = ,即 = ,∴BD=4 cm;
(3)∵△CBD∽△ABC,
∴ = ,即 = ,BD= =9 cm.
A
B
C
D
随堂练习
2.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8 cm,A′D′=3 cm.则△ABC与△A′B′C′对应高的比为_______.
C
8:3
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=4 m,点P到CD的距离是3 m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
4.如图,在△ABC中,内接矩形DEFG的一边DE在BC上,AH是BC上的高,AH交GF于点K,BC=48,EF=10,DE=18.求AK的长.
解:∵四边形DEFG为矩形,
∴GF∥BC,GF=DE=18,KH=FE=10,
∴△AGF∽△ABC,
∴ = ,即 = ,
∴AK=6.
A
B
C
D
E
F
G
H
K
5.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
解:∵△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2 cm.
A
G
B
C
D
E
F
H
6.如图,△ABC是一张锐角三角形硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
(2)求矩形EFGH的周长.
解:(1)易得AM⊥HG,
∵四边形EFGH为矩形,
∴EF∥GH,
∴∠AHG=∠ABC.
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∴
(2)由(1)得:
设HE=x cm,则MD=HE=x cm,
∵AD=30 cm,∴AM=(30-x) cm.
∵HG=2HE,∴HG=2x cm,
解得,x=12,2x=24,
所以矩形EFGH的周长为:2×(12+24)=72(cm).
课堂小结
北师大版 九年级上册
4.7 相似三角形的性质
第1课时 相似三角形中的对应线段之比
情景导入
1.什么叫相似三角形?相似比指的是什么?
2.全等三角形是相似三角形吗?全等三角形的相似比是什么?
3.相似三角形的判定方法有哪些?
4.根据相似三角形的概念可知相似三角形有哪些性质?
5.相似三角形还有其他的性质吗?
实践探究
探究1
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1 : 2的比例建造了模型房的房梁△A′B′C′,CD和C′D′分别是它们的立柱.
A
B
C
D
A′
B′
C′
D′
思考
问题1:试写出△ABC与△A′B′C′的对应边之间的关系和对应角之间的关系.
问题2:△ACD与△A′C′D′相似吗?为什么?如果相似,指出它们的相似比.
A
B
C
D
A′
B′
C′
D′
问题3:如果CD=1.5 cm,那么模型房的房梁立柱有多高?
问题4:据此,你可以发现相似三角形具有怎样的性质?
相似三角形对应高的比等于相似比.
归纳
A
B
C
D
A′
B′
C′
D′
探究2:探索相似三角形对应线段的比
思考
已知:△ABC ∽△A′B′C′,相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?请证明你的结论。
A
B
C
A′
B′
C′
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出△ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A′
B′
C′
D
D′
∴ = =k,
A
B
C
F
A′
B′
C′
F′
A
B
C
E
A′
B′
C′
E′
相似三角形对应角的角平分线之比等于相似比.
相似三角形对应边上的中线比等于相似比.
归纳总结
1.相似三角形对应边的比等于________.
2.相似三角形的各对应角_______,各对应边_________.
3.相似三角形对应高的比、对应__________的比、对应________的比都等于相似比.
相似比
相等
成比例
角平分线
中线
应用举例
例1
如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR= BC时,求DE的长.如果SR= BC呢?
方法指导:相似三角形的判定及相似三角形的性质.
B
A
E
R
C
D
S
解:∵SR⊥AD,BC⊥AD,
∴SR∥BC.
∴∠ASR=∠B,∠ARS=∠C.
(相似三角形对应高的比等于相似比),
∴△ASR∽△ABC
(两角分别相等的两个三角形相似).
B
A
E
R
C
D
S
B
A
E
R
C
D
S
如图,CD是Rt△ABC 的斜边AB上的高.
(1)则图中有几对相似三角形?
(2)若AD=9 cm,CD=6 cm,求BD;
(3)若AB=25 cm,BC=15 cm,求BD.
方法指导:相似三角形的判定和性质的综合应用.
例2
A
B
C
D
解:(1)∵CD⊥AB,
∴∠ADC=∠BDC=∠ACB=90°.
在△ADC和△ACB中,∠ADC=∠ACB=90°,∠A=∠A,∴△ADC∽△ACB,
同理可知,△CDB∽△ACB,△ADC∽△CDB.
所以图中有三对相似三角形;
A
B
C
D
(2)∵△ACD∽△CBD,
∴ = ,即 = ,∴BD=4 cm;
(3)∵△CBD∽△ABC,
∴ = ,即 = ,BD= =9 cm.
A
B
C
D
随堂练习
2.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8 cm,A′D′=3 cm.则△ABC与△A′B′C′对应高的比为_______.
C
8:3
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=4 m,点P到CD的距离是3 m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
4.如图,在△ABC中,内接矩形DEFG的一边DE在BC上,AH是BC上的高,AH交GF于点K,BC=48,EF=10,DE=18.求AK的长.
解:∵四边形DEFG为矩形,
∴GF∥BC,GF=DE=18,KH=FE=10,
∴△AGF∽△ABC,
∴ = ,即 = ,
∴AK=6.
A
B
C
D
E
F
G
H
K
5.已知△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm.求EH的长.
解:∵△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2 cm.
A
G
B
C
D
E
F
H
6.如图,△ABC是一张锐角三角形硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
(2)求矩形EFGH的周长.
解:(1)易得AM⊥HG,
∵四边形EFGH为矩形,
∴EF∥GH,
∴∠AHG=∠ABC.
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∴
(2)由(1)得:
设HE=x cm,则MD=HE=x cm,
∵AD=30 cm,∴AM=(30-x) cm.
∵HG=2HE,∴HG=2x cm,
解得,x=12,2x=24,
所以矩形EFGH的周长为:2×(12+24)=72(cm).
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
