4.8.2 平面直角坐标系中的位似变换 课件(共21张PPT)
文档属性
| 名称 | 4.8.2 平面直角坐标系中的位似变换 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 08:56:53 | ||
图片预览







文档简介
(共21张PPT)
北师大版 九年级上册
4.8 图形的位似
第2课时 平面直角坐标系中的位似变换
情景导入
如图,已知点A(0,3),B(2,0)是平面直角坐标系内的两点,连接AB.
(1)将线段AB向左平移2个单位长度得到线段A1B1,画出图形,并写出点A1,B1的坐标;
(2)作出线段AB关于y轴对称的线段A2B2,并写出点A2,B2的坐标;
(3)将线段AB绕原点O旋转180°得到线段A3B3,画出图形,并写出点A3,B3的坐标;
(4)以原点O为位似中心,位似比为 ,把线段AB缩小,得到线段A4B4,请在图中画出线段A4B4,写出点A4,B4的坐标.观察对应点坐标的变化,你有什么发现?
x
y
O
1
2
3
4
-4
-3
-2
-1
-1
-2
-3
-4
1
2
3
4
A
B
解:(1)线段A1B1如图所示,
A1(-2,3),B1(0,0);
(2)A2(0,3),B2(-2,0);
(3)A3(0,-3),B3(-2,0);
(4)A4(0,1.5),B4(1,0);
点A,B的横、纵坐标都乘 得到点A4,B4的横、纵坐标.
x
y
O
1
2
3
4
-4
-3
-2
-1
-1
-2
-3
-4
1
2
3
4
A
B
A1
B1
实践探究
在直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(3,0),B(2,3).按要求完成下列问题:
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
将点O,A,B的横、纵坐标都乘以2,得到三个点O′,A′,B′,请你在坐标系中找到这三个点.
将点O,A,B的横、纵坐标都乘2,
得到O′ ( ),A′ ( ),B′ ( )
0,0
4,6
6,0
(O′)
探究1
(3)如果位似,指出位似中心和相似比.
(2)以这三个点为顶点的三角形与△OAB位似吗?为什么?
△OAB和△OA′B′是位似的
位似中心是点O,相似比是2.
它们对应顶点所在的直线相交于一点O.
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
(O′)
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
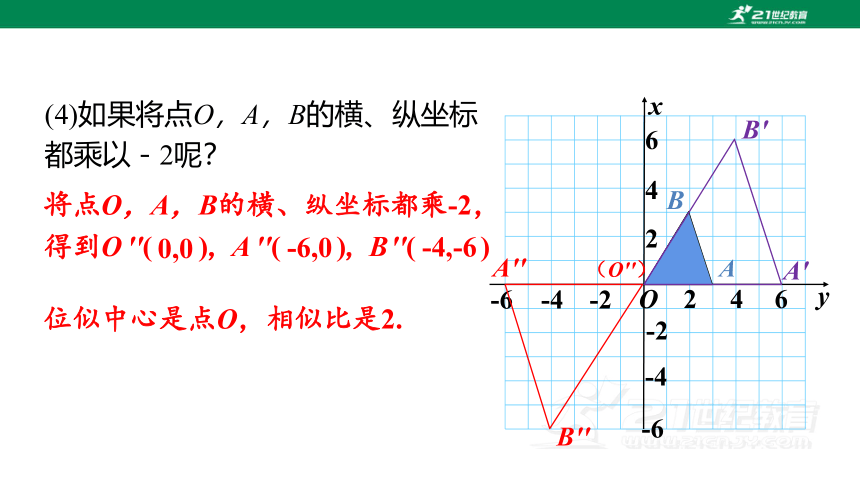
(4)如果将点O,A,B的横、纵坐标都乘以-2呢?
A′′
B′′
将点O,A,B的横、纵坐标都乘-2,得到O ′′( ),A ′′( ),B ′′( )
0,0
-6,0
-4,-6
(O′′)
位似中心是点O,相似比是2.
归纳总结
在平面直角坐标系中,将一个三角形每个顶点的横坐标、纵坐标都乘同一个数 k ( k≠0 ),所得的图形与原图形________,位似中心是___________,它们的相似比为_____.
位似
坐标原点
|k|
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
C
探究2
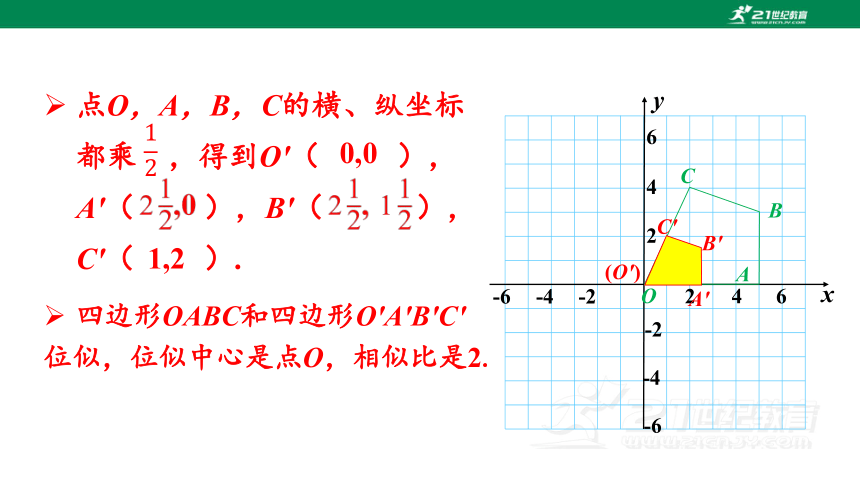
点O,A,B,C的横、纵坐标都乘 ,得到O'( ),A'( ),B'( ),C'( ).
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
C
0,0
1,2
A'
B'
C'
(O')
四边形OABC和四边形O'A'B'C'
位似,位似中心是点O,相似比是2.
归纳总结
在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k (k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为 | k |.
应用举例
在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(6,0),B(3,6),
C(-3,3).以原点O为位似中心画一个四边形,使它与四边形OABC位似,且相似比是2 : 3.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
例1
用线段顺次连接点O ,A′,B′,C′,O,则四边形OA′B′C′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
B’
C’
A’
方法一:
用线段顺次连接点O ,A′′,B′′,C′′,O,则四边形OA′′B′′C′′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
B’
C’
A’
B’’
C’’
A’’
方法二:
随堂练习
1.在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),四边形O1A1B1C1是以点O为位似中心且与四边形OABC的相似比是2 : 1,点O1,A1,B1,C1的坐标分别是____________________________________________
___________________________________________.
O1(0,0),A1(6,0)或(-6,0),B1(8,8)或
(-8,-8),C1(-4,6)或(4,-6)
2.△ABC的三个顶点坐标分别为A(2,2),B(4,2),C(6,4),以原点为位似中心,将△ABC缩小后得到的△DEF与△ABC对应边的比为1 : 2,且两个三角形在位似中心的同侧,则△DEF各顶点的坐标分别为___________________________.
D(1,1),E(2,1),F(3,2)
3.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.
若点A的坐标是(1,2),则点A′的坐标
是( )
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
C
4. 在 13×13 的网格图中,已知△ABC 和点 M (1,2).
(1) 以点 M 为位似中心,位似比为 2,画出△ABC的位似图形△A′B′C′;
x
y
A
B
C
M
A′
B′
C′
解:如图所示.
(2) 写出△A′B′C′ 的各顶点坐标.
答:△A′B′C′的各顶点坐标分别为A′ (3,6),B′ (5,2),C′ (11,4).
5.如图,在直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3).画出四边形OABC以O为位似中心的位似图形,使它与四边形OABC的相似比是2 : 1.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
A
B
C
8
-6
-8
四边形OABC的顶点坐标都乘2 分别是O(0,0),A′(6,0),B′(8,8),C′(-4,6);在平面直角坐标系中描出点A′,B′,C′,用线段顺次连接点O ,A′,B′,C′,O,则四边形OA′B′C′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
A
B
C
8
-6
-8
A’
B’
C’
O
x
y
2
4
6
2
4
6
-2
-4
A
B
C
8
-6
-8
A’
C’
B’
-2
-4
-6
四边形OABC的顶点坐标都乘-2分别是O(0,0),A′′(-6,0),B′′
(-8,-8),C′′ (4,-6);在平面直角坐标系中描出点A′′,B′′,C′′,用线段顺次连接点O ,A′′,B′′,C′′,O,则四边形OA′′B′′C′′就是符合要求的四边形.
A′′
B′′
D′′
课堂小结
北师大版 九年级上册
4.8 图形的位似
第2课时 平面直角坐标系中的位似变换
情景导入
如图,已知点A(0,3),B(2,0)是平面直角坐标系内的两点,连接AB.
(1)将线段AB向左平移2个单位长度得到线段A1B1,画出图形,并写出点A1,B1的坐标;
(2)作出线段AB关于y轴对称的线段A2B2,并写出点A2,B2的坐标;
(3)将线段AB绕原点O旋转180°得到线段A3B3,画出图形,并写出点A3,B3的坐标;
(4)以原点O为位似中心,位似比为 ,把线段AB缩小,得到线段A4B4,请在图中画出线段A4B4,写出点A4,B4的坐标.观察对应点坐标的变化,你有什么发现?
x
y
O
1
2
3
4
-4
-3
-2
-1
-1
-2
-3
-4
1
2
3
4
A
B
解:(1)线段A1B1如图所示,
A1(-2,3),B1(0,0);
(2)A2(0,3),B2(-2,0);
(3)A3(0,-3),B3(-2,0);
(4)A4(0,1.5),B4(1,0);
点A,B的横、纵坐标都乘 得到点A4,B4的横、纵坐标.
x
y
O
1
2
3
4
-4
-3
-2
-1
-1
-2
-3
-4
1
2
3
4
A
B
A1
B1
实践探究
在直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(3,0),B(2,3).按要求完成下列问题:
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
将点O,A,B的横、纵坐标都乘以2,得到三个点O′,A′,B′,请你在坐标系中找到这三个点.
将点O,A,B的横、纵坐标都乘2,
得到O′ ( ),A′ ( ),B′ ( )
0,0
4,6
6,0
(O′)
探究1
(3)如果位似,指出位似中心和相似比.
(2)以这三个点为顶点的三角形与△OAB位似吗?为什么?
△OAB和△OA′B′是位似的
位似中心是点O,相似比是2.
它们对应顶点所在的直线相交于一点O.
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
(O′)
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
A′
B′
(4)如果将点O,A,B的横、纵坐标都乘以-2呢?
A′′
B′′
将点O,A,B的横、纵坐标都乘-2,得到O ′′( ),A ′′( ),B ′′( )
0,0
-6,0
-4,-6
(O′′)
位似中心是点O,相似比是2.
归纳总结
在平面直角坐标系中,将一个三角形每个顶点的横坐标、纵坐标都乘同一个数 k ( k≠0 ),所得的图形与原图形________,位似中心是___________,它们的相似比为_____.
位似
坐标原点
|k|
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
C
探究2
点O,A,B,C的横、纵坐标都乘 ,得到O'( ),A'( ),B'( ),C'( ).
O
x
y
2
4
6
2
4
6
-2
-4
-6
-2
-4
-6
A
B
C
0,0
1,2
A'
B'
C'
(O')
四边形OABC和四边形O'A'B'C'
位似,位似中心是点O,相似比是2.
归纳总结
在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k (k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为 | k |.
应用举例
在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(6,0),B(3,6),
C(-3,3).以原点O为位似中心画一个四边形,使它与四边形OABC位似,且相似比是2 : 3.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
例1
用线段顺次连接点O ,A′,B′,C′,O,则四边形OA′B′C′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
B’
C’
A’
方法一:
用线段顺次连接点O ,A′′,B′′,C′′,O,则四边形OA′′B′′C′′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
B
C
8
-6
-8
A
B’
C’
A’
B’’
C’’
A’’
方法二:
随堂练习
1.在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),四边形O1A1B1C1是以点O为位似中心且与四边形OABC的相似比是2 : 1,点O1,A1,B1,C1的坐标分别是____________________________________________
___________________________________________.
O1(0,0),A1(6,0)或(-6,0),B1(8,8)或
(-8,-8),C1(-4,6)或(4,-6)
2.△ABC的三个顶点坐标分别为A(2,2),B(4,2),C(6,4),以原点为位似中心,将△ABC缩小后得到的△DEF与△ABC对应边的比为1 : 2,且两个三角形在位似中心的同侧,则△DEF各顶点的坐标分别为___________________________.
D(1,1),E(2,1),F(3,2)
3.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.
若点A的坐标是(1,2),则点A′的坐标
是( )
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
C
4. 在 13×13 的网格图中,已知△ABC 和点 M (1,2).
(1) 以点 M 为位似中心,位似比为 2,画出△ABC的位似图形△A′B′C′;
x
y
A
B
C
M
A′
B′
C′
解:如图所示.
(2) 写出△A′B′C′ 的各顶点坐标.
答:△A′B′C′的各顶点坐标分别为A′ (3,6),B′ (5,2),C′ (11,4).
5.如图,在直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3).画出四边形OABC以O为位似中心的位似图形,使它与四边形OABC的相似比是2 : 1.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
A
B
C
8
-6
-8
四边形OABC的顶点坐标都乘2 分别是O(0,0),A′(6,0),B′(8,8),C′(-4,6);在平面直角坐标系中描出点A′,B′,C′,用线段顺次连接点O ,A′,B′,C′,O,则四边形OA′B′C′就是符合要求的四边形.
O
x
y
2
4
6
2
4
6
-2
-4
-2
-4
-6
A
B
C
8
-6
-8
A’
B’
C’
O
x
y
2
4
6
2
4
6
-2
-4
A
B
C
8
-6
-8
A’
C’
B’
-2
-4
-6
四边形OABC的顶点坐标都乘-2分别是O(0,0),A′′(-6,0),B′′
(-8,-8),C′′ (4,-6);在平面直角坐标系中描出点A′′,B′′,C′′,用线段顺次连接点O ,A′′,B′′,C′′,O,则四边形OA′′B′′C′′就是符合要求的四边形.
A′′
B′′
D′′
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
