5.1.2 平行投影 课件(共30张PPT)
文档属性
| 名称 | 5.1.2 平行投影 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 10:42:05 | ||
图片预览







文档简介
(共30张PPT)
北师大版 九年级上册
5.1 投 影
第2课时 平行投影
情景导入
物体在日光或灯光的照射下会在地面、墙壁等处形成影子,请观察下面三幅图片,感受日常生活中的投影现象.
问题:物体在太阳光下形成的影子与在灯光下形成的影子有什么不同?
实践探究
探究1:平行投影、正投影的概念
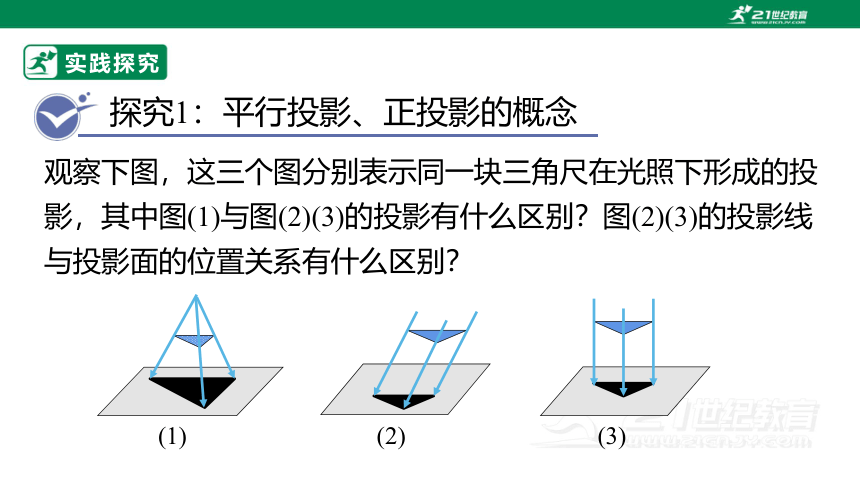
观察下图,这三个图分别表示同一块三角尺在光照下形成的投影,其中图(1)与图(2)(3)的投影有什么区别?图(2)(3)的投影线与投影面的位置关系有什么区别?
(1)
(2)
(3)
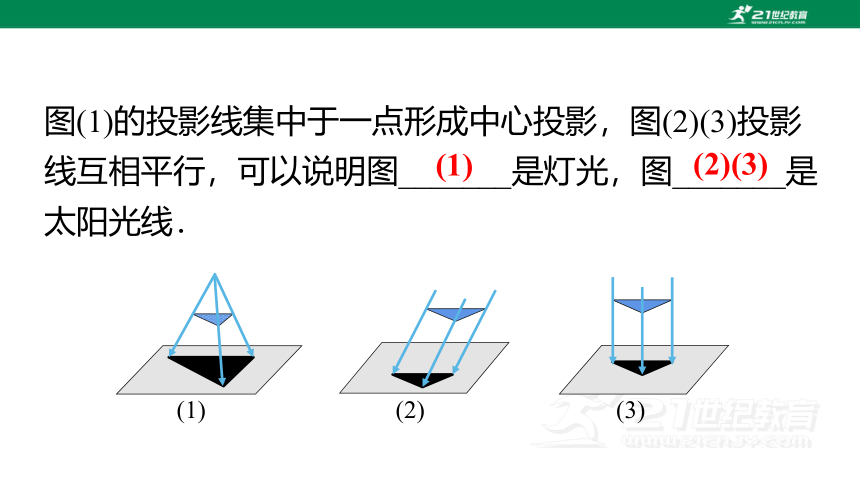
图(1)的投影线集中于一点形成中心投影,图(2)(3)投影线互相平行,可以说明图_______是灯光,图_______是太阳光线.
(1)
(2)(3)
(1)
(2)
(3)
(1)灯光是由_________发出的,灯光下的影子是______
______,太阳光是___________;
(2)物体在___________下形成的投影称为平行投影;
(3)在平行投影中,平行线与投影面_______的光线,称为正投影.图______是正投影.
归纳总结
一点
中心
平行光线
平行光线
垂直
(3)
投影
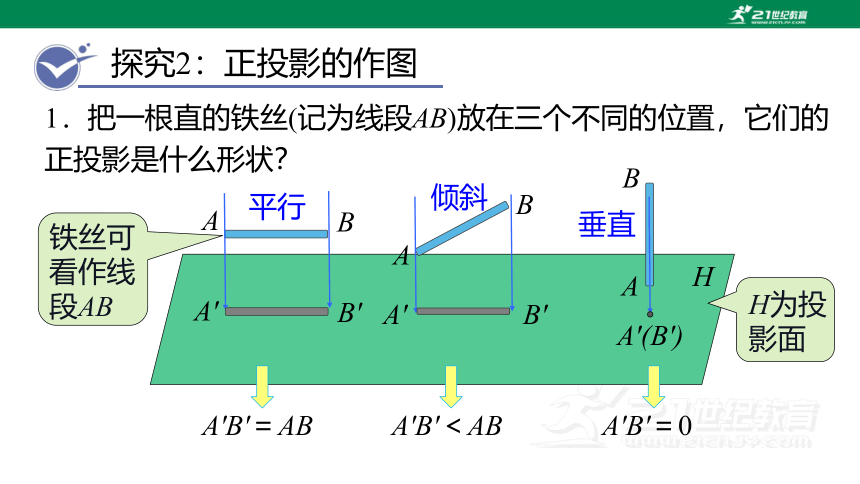
1.把一根直的铁丝(记为线段AB)放在三个不同的位置,它们的正投影是什么形状?
探究2:正投影的作图
H
A
B
A
B
A
B
铁丝可看作线段AB
A'
B'
A'
B'
A'(B')
H为投影面
A'B'=AB
A'B'<AB
A'B'=0
平行
倾斜
垂直
归纳总结
线段正投影有如下规律:
平行长不变,
倾斜长缩短,
垂直成一点.
练一练
(1)木棒长为1.2m,则它的正投影的长一定( )
A. 大于1.2m B. 小于1.2m
C. 等于1.2m D. 小于或等于1.2m
(2)在同一时刻,两根长度不等的木杆置于阳光下,但它们的影长相等,则它们的相对位置是( )
A. 一根垂直于地面 B. 两根都平行斜插在地面上
C. 两根木杆不平行 D. 一根倒在地上
D
C
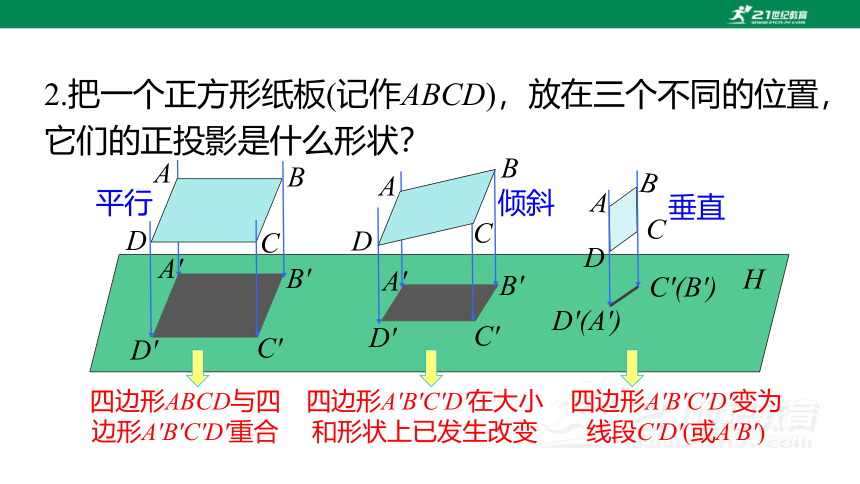
2.把一个正方形纸板(记作ABCD),放在三个不同的位置,它们的正投影是什么形状?
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形ABCD与四边形A'B'C'D'重合
四边形A'B'C'D'在大小和形状上已发生改变
四边形A'B'C'D'变为线段C'D'(或A'B')
归纳总结
平面图形的正投影有如下规律:
平行形不变,
倾斜形改变,
垂直成线段.
练一练
(1)皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是( )
D
A
B
C
D
(2)小明同学拿着一个如图所示的三角形木架在太阳光下玩,他不断变换三角形木架的位置,他说他发现了三角形木架在地上出现过的影子有四种:①点;②线段;③三角形;④四边形.你认为小明说法中正确的有_______(填序号).
②③
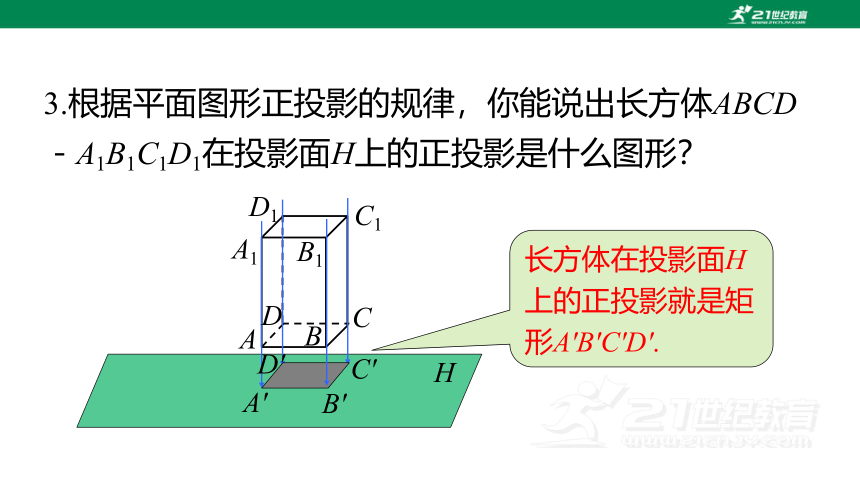
3.根据平面图形正投影的规律,你能说出长方体ABCD-A1B1C1D1在投影面H上的正投影是什么图形?
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体在投影面H上的正投影就是矩形A'B'C'D'.
归纳总结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
练一练
1.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A. 圆 B. 圆柱 C. 梯形 D. 矩形
2.底面与投影面垂直的圆锥体的正投影是( )
A. 圆 B. 三角形 C. 矩形 D. 正方形
D
B
探究3:物体的影子与它们高度之间的关系
1.在三个不同时刻,同一棵树的影子长度______,在上午随时间的推移,影子的长度逐渐变_____;在下午随时间的推移,影子的长度逐渐变_____,顺序为______________.
2.在同一时刻,大树高度与其影长之比_______小树高度与其影长之比.
不同
短
长
丙、乙、甲
等于
在同一时刻,物体的影子与它们的高度成正比例.
归纳
应用举例
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(甲)
(乙)
A
D
D
B
E
E
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
例1
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:因为△ADD
∽△BEE ,所以
AD=1.86m
所以,甲木杆的高度为1.86m.
如图,分别是两棵树及其影子的情形.
(1)哪个图是阳光下的情景?哪个图是路灯下的情景?
(2)你是用什么方法判断的?
例2
方法指导:平行投影与中心投影的区别.
①
②
解:(1)第①幅图是阳光下的情景(平行投影),
第②幅图是路灯下的情景(中心投影);
(2)第①幅图物高与影长成比例,第②幅图不成比例.
①
②
例3
下面四幅图是两个物体在不同时刻太阳光下的影子,按照时间的先后顺序正确的是 ( )
A.①②③④ B.③①②④ C.③④①② D.②④③①
①
②
③
④
方法指导:太阳从东边升起,影子指向西方,然后影长逐渐变小,过了正午,影子又逐渐变长.
C
随堂练习
1.以下四幅图中,表示两棵小树在同一时刻阳光下的影子的是 ( )
A
B
C
D
D
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A. 逐渐变短
B. 逐渐变长
C. 先变短后变长
D. 先变长后变短
C
3.如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=3 m,在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,则DE的长为________.
10 m
4. 就北半球而言,从早晨到傍晚,物体影子的指向是:上午向西,下午______;影长的变化情况是:上午日影越来越_____,下午日影越来越_____.
向东
短
长
5.如图,木棒AB在投影面P上的正投影为A1B1,且AB=10 cm,∠BAA1=120°,试求投影A1B1的长.
解:如图,过点A作AC⊥BB1,垂足为点C.
易得四边形AA1B1C为矩形,
∴∠A1AC=90°,AC=A1B1.
∵∠BAA1=120°,
∴∠BAC=120°-90°=30°,
∴在Rt△ABC中,BC= AB=5(cm),
则AC= =5 (cm).
∴A1B1=AC=5 cm.
6.小明同学在学习了相似三角形的知识后,就想利用树影测量树高,但这棵树离楼房太近,影子不全落在地上,有一部分影子落在墙上,如图,在某时刻测留在墙上的影子长为1.2m,测得地面影长4.9m,巧的是他拿的竹竿的长也是1.2m,竹竿的影长1.05m,你知道小明是怎样求树高AB的吗?你知道结果是多少吗?
解:设树高AB为xm,延长AD交地面于E,
解得 x=6.8.
E
7.一位同学想利用树影测树高,已知在某一时刻直立于地面的长1.5m的竹竿的影长为3m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高CD=1.2m,地面部分影长BD=5.4m,求树高AB.
A
B
D
C
E
方法一:
解:过点D作DE∥AC交AB于点E.
∵四边形AEDC为平行四边形,
∴AE=CD=1.2m.
∴AB=AE+EB=3.9m.
∴树高AB为3.9m.
方法二:
解:延长AC交BD的延长线于点E.
∴BE=BD+DE=7.8m.
∴树高AB为3.9m.
E
B
D
C
A
课堂小结
平行投影
与
正投影
概念:平行光线所形成的投影
平行投影
正
投
影
画法
计算
线段的
正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
影长≤线段长
平行形不变,倾斜形改变,垂直成线段
平面图形
视图
北师大版 九年级上册
5.1 投 影
第2课时 平行投影
情景导入
物体在日光或灯光的照射下会在地面、墙壁等处形成影子,请观察下面三幅图片,感受日常生活中的投影现象.
问题:物体在太阳光下形成的影子与在灯光下形成的影子有什么不同?
实践探究
探究1:平行投影、正投影的概念
观察下图,这三个图分别表示同一块三角尺在光照下形成的投影,其中图(1)与图(2)(3)的投影有什么区别?图(2)(3)的投影线与投影面的位置关系有什么区别?
(1)
(2)
(3)
图(1)的投影线集中于一点形成中心投影,图(2)(3)投影线互相平行,可以说明图_______是灯光,图_______是太阳光线.
(1)
(2)(3)
(1)
(2)
(3)
(1)灯光是由_________发出的,灯光下的影子是______
______,太阳光是___________;
(2)物体在___________下形成的投影称为平行投影;
(3)在平行投影中,平行线与投影面_______的光线,称为正投影.图______是正投影.
归纳总结
一点
中心
平行光线
平行光线
垂直
(3)
投影
1.把一根直的铁丝(记为线段AB)放在三个不同的位置,它们的正投影是什么形状?
探究2:正投影的作图
H
A
B
A
B
A
B
铁丝可看作线段AB
A'
B'
A'
B'
A'(B')
H为投影面
A'B'=AB
A'B'<AB
A'B'=0
平行
倾斜
垂直
归纳总结
线段正投影有如下规律:
平行长不变,
倾斜长缩短,
垂直成一点.
练一练
(1)木棒长为1.2m,则它的正投影的长一定( )
A. 大于1.2m B. 小于1.2m
C. 等于1.2m D. 小于或等于1.2m
(2)在同一时刻,两根长度不等的木杆置于阳光下,但它们的影长相等,则它们的相对位置是( )
A. 一根垂直于地面 B. 两根都平行斜插在地面上
C. 两根木杆不平行 D. 一根倒在地上
D
C
2.把一个正方形纸板(记作ABCD),放在三个不同的位置,它们的正投影是什么形状?
H
A
B
D
C
A'
B'
C'
D'
A'
B'
C'
D'
A
B
D
C
平行
倾斜
垂直
D'(A')
C'(B')
A
B
D
C
四边形ABCD与四边形A'B'C'D'重合
四边形A'B'C'D'在大小和形状上已发生改变
四边形A'B'C'D'变为线段C'D'(或A'B')
归纳总结
平面图形的正投影有如下规律:
平行形不变,
倾斜形改变,
垂直成线段.
练一练
(1)皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是( )
D
A
B
C
D
(2)小明同学拿着一个如图所示的三角形木架在太阳光下玩,他不断变换三角形木架的位置,他说他发现了三角形木架在地上出现过的影子有四种:①点;②线段;③三角形;④四边形.你认为小明说法中正确的有_______(填序号).
②③
3.根据平面图形正投影的规律,你能说出长方体ABCD-A1B1C1D1在投影面H上的正投影是什么图形?
H
A1
B1
C1
D1
A
B
C
D
A'
B'
C'
D'
长方体在投影面H上的正投影就是矩形A'B'C'D'.
归纳总结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
练一练
1.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A. 圆 B. 圆柱 C. 梯形 D. 矩形
2.底面与投影面垂直的圆锥体的正投影是( )
A. 圆 B. 三角形 C. 矩形 D. 正方形
D
B
探究3:物体的影子与它们高度之间的关系
1.在三个不同时刻,同一棵树的影子长度______,在上午随时间的推移,影子的长度逐渐变_____;在下午随时间的推移,影子的长度逐渐变_____,顺序为______________.
2.在同一时刻,大树高度与其影长之比_______小树高度与其影长之比.
不同
短
长
丙、乙、甲
等于
在同一时刻,物体的影子与它们的高度成正比例.
归纳
应用举例
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(甲)
(乙)
A
D
D
B
E
E
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
例1
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别为1.24m和1m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:因为△ADD
∽△BEE ,所以
AD=1.86m
所以,甲木杆的高度为1.86m.
如图,分别是两棵树及其影子的情形.
(1)哪个图是阳光下的情景?哪个图是路灯下的情景?
(2)你是用什么方法判断的?
例2
方法指导:平行投影与中心投影的区别.
①
②
解:(1)第①幅图是阳光下的情景(平行投影),
第②幅图是路灯下的情景(中心投影);
(2)第①幅图物高与影长成比例,第②幅图不成比例.
①
②
例3
下面四幅图是两个物体在不同时刻太阳光下的影子,按照时间的先后顺序正确的是 ( )
A.①②③④ B.③①②④ C.③④①② D.②④③①
①
②
③
④
方法指导:太阳从东边升起,影子指向西方,然后影长逐渐变小,过了正午,影子又逐渐变长.
C
随堂练习
1.以下四幅图中,表示两棵小树在同一时刻阳光下的影子的是 ( )
A
B
C
D
D
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A. 逐渐变短
B. 逐渐变长
C. 先变短后变长
D. 先变长后变短
C
3.如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=3 m,在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,则DE的长为________.
10 m
4. 就北半球而言,从早晨到傍晚,物体影子的指向是:上午向西,下午______;影长的变化情况是:上午日影越来越_____,下午日影越来越_____.
向东
短
长
5.如图,木棒AB在投影面P上的正投影为A1B1,且AB=10 cm,∠BAA1=120°,试求投影A1B1的长.
解:如图,过点A作AC⊥BB1,垂足为点C.
易得四边形AA1B1C为矩形,
∴∠A1AC=90°,AC=A1B1.
∵∠BAA1=120°,
∴∠BAC=120°-90°=30°,
∴在Rt△ABC中,BC= AB=5(cm),
则AC= =5 (cm).
∴A1B1=AC=5 cm.
6.小明同学在学习了相似三角形的知识后,就想利用树影测量树高,但这棵树离楼房太近,影子不全落在地上,有一部分影子落在墙上,如图,在某时刻测留在墙上的影子长为1.2m,测得地面影长4.9m,巧的是他拿的竹竿的长也是1.2m,竹竿的影长1.05m,你知道小明是怎样求树高AB的吗?你知道结果是多少吗?
解:设树高AB为xm,延长AD交地面于E,
解得 x=6.8.
E
7.一位同学想利用树影测树高,已知在某一时刻直立于地面的长1.5m的竹竿的影长为3m,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高CD=1.2m,地面部分影长BD=5.4m,求树高AB.
A
B
D
C
E
方法一:
解:过点D作DE∥AC交AB于点E.
∵四边形AEDC为平行四边形,
∴AE=CD=1.2m.
∴AB=AE+EB=3.9m.
∴树高AB为3.9m.
方法二:
解:延长AC交BD的延长线于点E.
∴BE=BD+DE=7.8m.
∴树高AB为3.9m.
E
B
D
C
A
课堂小结
平行投影
与
正投影
概念:平行光线所形成的投影
平行投影
正
投
影
画法
计算
线段的
正投影
平面图形的正投影
几何体的正投影
平行长不变,倾斜长变短,垂直成一点
影长≤线段长
平行形不变,倾斜形改变,垂直成线段
平面图形
视图
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
