活动单导学课程 苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.2双曲线的几何性质(2)(有答案)
文档属性
| 名称 | 活动单导学课程 苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.2双曲线的几何性质(2)(有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 00:00:00 | ||
图片预览


文档简介
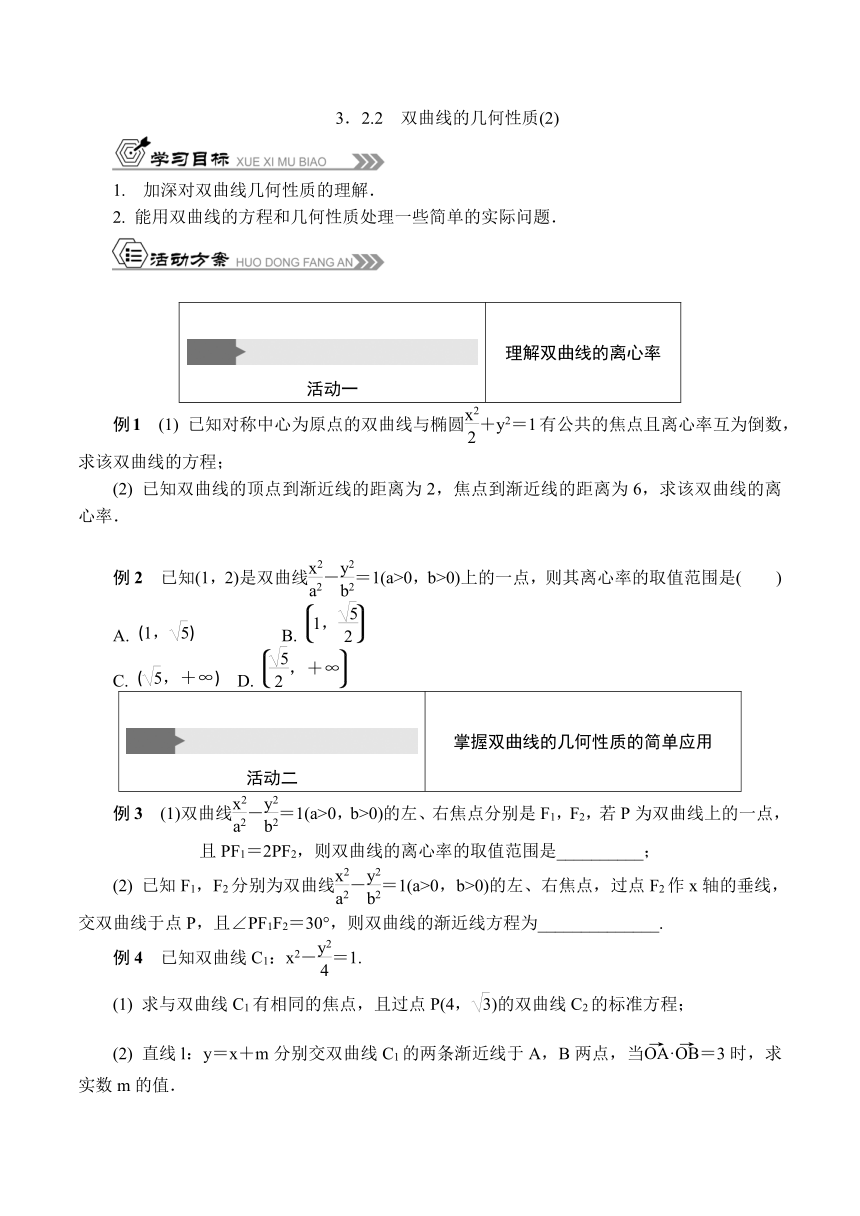
3.2.2 双曲线的几何性质(2)
1. 加深对双曲线几何性质的理解.
2. 能用双曲线的方程和几何性质处理一些简单的实际问题.
活动一 理解双曲线的离心率
例1 (1) 已知对称中心为原点的双曲线与椭圆+y2=1有公共的焦点且离心率互为倒数,求该双曲线的方程;
(2) 已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,求该双曲线的离心率.
例2 已知(1,2)是双曲线-=1(a>0,b>0)上的一点,则其离心率的取值范围是( )
A. B.
C. D.
活动二 掌握双曲线的几何性质的简单应用
例3 (1)双曲线-=1(a>0,b>0)的左、右焦点分别是F1,F2,若P为双曲线上的一点,且PF1=2PF2,则双曲线的离心率的取值范围是__________;
(2) 已知F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,过点F2作x轴的垂线,交双曲线于点P,且∠PF1F2=30°,则双曲线的渐近线方程为______________.
例4 已知双曲线C1:x2-=1.
(1) 求与双曲线C1有相同的焦点,且过点P(4,)的双曲线C2的标准方程;
(2) 直线l:y=x+m分别交双曲线C1的两条渐近线于A,B两点,当·=3时,求实数m的值.
活动三 双曲线方程的简单实际应用
例5 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行护航任务,对商船进行护航.某日,甲舰在乙舰正东方向6 km处,丙舰在乙舰北偏西30°方向,相距4 km处,某时刻甲舰发现商船的求救信号,由于乙、丙两舰比甲舰距商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s,若甲舰赶赴救援,行进的方向角应是多少?
反 思 与 感 悟
根据实际情况建立适当的平面直角坐标系,然后利用待定系数法求出双曲线的标准方程.
1. 双曲线x2-y2=1的顶点到其渐近线的距离为( )
A. B. C. 1 D.
2. 已知双曲线C:-=1(a>0,b>0)的焦距为10,点P(2,1)在双曲线C的渐近线上,则双曲线C的方程为( )
A. -=1 B. -=1 C. -=1 D. -=1
3. (多选)已知双曲线C:-=1过点(3,),则下列结论中正确的是( )
A. 双曲线C的焦距为4
B. 双曲线C的离心率为
C. 双曲线C的渐近线方程为y=±x
D. 直线2x-y-1=0与双曲线C有两个公共点
4. 设双曲线x2-=1的左、右焦点分别为F1,F2,直线x=1与双曲线的其中一条渐近线交于点P,则△PF1F2的面积是________.
5. 过双曲线C:-=1(a>0,b>0)的右焦点作一条与其渐近线平行的直线,交双曲线C于点P.若点P 的横坐标为2a,求双曲线C的离心率.
参考答案与解析
【活动方案】
例1 (1) 由题意,得椭圆的焦点坐标为(1,0),(-1,0),离心率e=,则双曲线的焦点坐标为(1,0),(-1,0),离心率为.
设双曲线的方程为-=1(a>0,b>0),
则c=1,a=,所以b2=1-=,
所以双曲线的方程为2x2-2y2=1.
(2) 不妨设双曲线的方程为-=1(a>0,b>0),
则顶点坐标为(a,0),一条渐近线方程为y=x,焦点坐标为(c,0).
所以解得所以e==3.
例2 C 解析:由(1,2)是双曲线-=1(a>0,b>0)上的一点,得-=1,则=b2+4,所以e===>,所以e>.
例3 (1) (1,3) 解析:由题意,得PF1-PF2=PF2=2a,则PF1=4a.在△PF1F2中,2a<2c<6a,所以1<<3.
(2) x±y=0 解析:由题意,得PF2=PF1,则PF1-PF2=PF1=2a,即PF1=4a,PF2=2a.在Rt△PF1F2中,∠PF1F2=30°,所以F1F2=2c=2a,即c=a,所以b=a,所以双曲线的渐近线方程为x±y=0.
例4 (1) 由题意,得双曲线C1的焦点坐标为(,0),(-,0).
设双曲线C2的标准方程为-=1(a>0,b>0),
则解得
所以双曲线C2的标准方程为-y2=1.
(2) 由题意,得双曲线C1的渐近线方程为y=±2x.
设点A(x1,2x1),B(x2,-2x2),
联立
消去y并整理,得3x2-2mx-m2=0,
由Δ=(-2m)2-4×3×(-m2)=16m2>0,
得m≠0.
因为x1x2=-,
所以·=x1x2+2x1(-2x2)=-3x1x2=m2,
所以m2=3,即m=±.
例5 设点A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图,以直线AB为x 轴,线段AB的垂直平分线为y 轴建立平面直角坐标系,则A(3,0),B(-3,0),C(-5,2).
因为PB=PC,所以点P在线段BC的垂直平分线上.
又易知kBC=-,线段BC的中点D(-4,),
所以直线PD的方程为y-=(x+4).①
又PB-PA=4,AB=6>4,
所以点P在以A,B为焦点的双曲线的右支上,
所以双曲线方程为-=1(x≥2).②
联立①②,得点P坐标为(8,5),
所以kPA==,
故甲舰行进的方向角为北偏东30°.
【检测反馈】
1. B 解析:双曲线x2-y2=1的渐近线方程为x±y=0,顶点坐标为(1,0),(-1,0),故顶点到渐近线的距离为.
2. A 解析:因为双曲线C的焦距为10,点P(2,1)在渐近线上,所以a2+b2=c2=25,=1,解得b2=5,a2=20,故双曲线C的方程为-=1.
3. AC 解析:由双曲线C:-=1过点(3,),可得m=1,则双曲线C的标准方程为-y2=1,所以a=,b=1,c==2,所以双曲线C的焦距为2c=4,故A正确;双曲线C的离心率为==,故B错误;双曲线C的渐近线方程为y=±x,故C正确;将2x-y-1=0与-y2=1联立,消去y可得3x2-4x+4=0,Δ=(-4)2-4×3×4=-32<0,所以直线2x-y-1=0与双曲线C没有公共点,故D错误.故选AC.
4. 3 解析:由双曲线方程知其渐近线方程为y=±3x,焦点F1(-,0),F2(,0),则直线x=1与双曲线的渐近线交于点(1,3),(1,-3).不妨设P(1,3),则S△PF1F2=×2×3=3.
5. 不妨设过右焦点且与渐近线平行的直线l的斜率为.
因为直线l过右焦点F(c,0),
所以直线l的方程为y=(x-c).
因为点P的横坐标为2a,
代入双曲线方程,得-=1,
化简,得y=-b或y=b(点P在x轴下方,故舍去),故点P的坐标为(2a,-b),
代入直线方程,得-b=(2a-c),
化简,得离心率e==2+.
1. 加深对双曲线几何性质的理解.
2. 能用双曲线的方程和几何性质处理一些简单的实际问题.
活动一 理解双曲线的离心率
例1 (1) 已知对称中心为原点的双曲线与椭圆+y2=1有公共的焦点且离心率互为倒数,求该双曲线的方程;
(2) 已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,求该双曲线的离心率.
例2 已知(1,2)是双曲线-=1(a>0,b>0)上的一点,则其离心率的取值范围是( )
A. B.
C. D.
活动二 掌握双曲线的几何性质的简单应用
例3 (1)双曲线-=1(a>0,b>0)的左、右焦点分别是F1,F2,若P为双曲线上的一点,且PF1=2PF2,则双曲线的离心率的取值范围是__________;
(2) 已知F1,F2分别为双曲线-=1(a>0,b>0)的左、右焦点,过点F2作x轴的垂线,交双曲线于点P,且∠PF1F2=30°,则双曲线的渐近线方程为______________.
例4 已知双曲线C1:x2-=1.
(1) 求与双曲线C1有相同的焦点,且过点P(4,)的双曲线C2的标准方程;
(2) 直线l:y=x+m分别交双曲线C1的两条渐近线于A,B两点,当·=3时,求实数m的值.
活动三 双曲线方程的简单实际应用
例5 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行护航任务,对商船进行护航.某日,甲舰在乙舰正东方向6 km处,丙舰在乙舰北偏西30°方向,相距4 km处,某时刻甲舰发现商船的求救信号,由于乙、丙两舰比甲舰距商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s,若甲舰赶赴救援,行进的方向角应是多少?
反 思 与 感 悟
根据实际情况建立适当的平面直角坐标系,然后利用待定系数法求出双曲线的标准方程.
1. 双曲线x2-y2=1的顶点到其渐近线的距离为( )
A. B. C. 1 D.
2. 已知双曲线C:-=1(a>0,b>0)的焦距为10,点P(2,1)在双曲线C的渐近线上,则双曲线C的方程为( )
A. -=1 B. -=1 C. -=1 D. -=1
3. (多选)已知双曲线C:-=1过点(3,),则下列结论中正确的是( )
A. 双曲线C的焦距为4
B. 双曲线C的离心率为
C. 双曲线C的渐近线方程为y=±x
D. 直线2x-y-1=0与双曲线C有两个公共点
4. 设双曲线x2-=1的左、右焦点分别为F1,F2,直线x=1与双曲线的其中一条渐近线交于点P,则△PF1F2的面积是________.
5. 过双曲线C:-=1(a>0,b>0)的右焦点作一条与其渐近线平行的直线,交双曲线C于点P.若点P 的横坐标为2a,求双曲线C的离心率.
参考答案与解析
【活动方案】
例1 (1) 由题意,得椭圆的焦点坐标为(1,0),(-1,0),离心率e=,则双曲线的焦点坐标为(1,0),(-1,0),离心率为.
设双曲线的方程为-=1(a>0,b>0),
则c=1,a=,所以b2=1-=,
所以双曲线的方程为2x2-2y2=1.
(2) 不妨设双曲线的方程为-=1(a>0,b>0),
则顶点坐标为(a,0),一条渐近线方程为y=x,焦点坐标为(c,0).
所以解得所以e==3.
例2 C 解析:由(1,2)是双曲线-=1(a>0,b>0)上的一点,得-=1,则=b2+4,所以e===>,所以e>.
例3 (1) (1,3) 解析:由题意,得PF1-PF2=PF2=2a,则PF1=4a.在△PF1F2中,2a<2c<6a,所以1<<3.
(2) x±y=0 解析:由题意,得PF2=PF1,则PF1-PF2=PF1=2a,即PF1=4a,PF2=2a.在Rt△PF1F2中,∠PF1F2=30°,所以F1F2=2c=2a,即c=a,所以b=a,所以双曲线的渐近线方程为x±y=0.
例4 (1) 由题意,得双曲线C1的焦点坐标为(,0),(-,0).
设双曲线C2的标准方程为-=1(a>0,b>0),
则解得
所以双曲线C2的标准方程为-y2=1.
(2) 由题意,得双曲线C1的渐近线方程为y=±2x.
设点A(x1,2x1),B(x2,-2x2),
联立
消去y并整理,得3x2-2mx-m2=0,
由Δ=(-2m)2-4×3×(-m2)=16m2>0,
得m≠0.
因为x1x2=-,
所以·=x1x2+2x1(-2x2)=-3x1x2=m2,
所以m2=3,即m=±.
例5 设点A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图,以直线AB为x 轴,线段AB的垂直平分线为y 轴建立平面直角坐标系,则A(3,0),B(-3,0),C(-5,2).
因为PB=PC,所以点P在线段BC的垂直平分线上.
又易知kBC=-,线段BC的中点D(-4,),
所以直线PD的方程为y-=(x+4).①
又PB-PA=4,AB=6>4,
所以点P在以A,B为焦点的双曲线的右支上,
所以双曲线方程为-=1(x≥2).②
联立①②,得点P坐标为(8,5),
所以kPA==,
故甲舰行进的方向角为北偏东30°.
【检测反馈】
1. B 解析:双曲线x2-y2=1的渐近线方程为x±y=0,顶点坐标为(1,0),(-1,0),故顶点到渐近线的距离为.
2. A 解析:因为双曲线C的焦距为10,点P(2,1)在渐近线上,所以a2+b2=c2=25,=1,解得b2=5,a2=20,故双曲线C的方程为-=1.
3. AC 解析:由双曲线C:-=1过点(3,),可得m=1,则双曲线C的标准方程为-y2=1,所以a=,b=1,c==2,所以双曲线C的焦距为2c=4,故A正确;双曲线C的离心率为==,故B错误;双曲线C的渐近线方程为y=±x,故C正确;将2x-y-1=0与-y2=1联立,消去y可得3x2-4x+4=0,Δ=(-4)2-4×3×4=-32<0,所以直线2x-y-1=0与双曲线C没有公共点,故D错误.故选AC.
4. 3 解析:由双曲线方程知其渐近线方程为y=±3x,焦点F1(-,0),F2(,0),则直线x=1与双曲线的渐近线交于点(1,3),(1,-3).不妨设P(1,3),则S△PF1F2=×2×3=3.
5. 不妨设过右焦点且与渐近线平行的直线l的斜率为.
因为直线l过右焦点F(c,0),
所以直线l的方程为y=(x-c).
因为点P的横坐标为2a,
代入双曲线方程,得-=1,
化简,得y=-b或y=b(点P在x轴下方,故舍去),故点P的坐标为(2a,-b),
代入直线方程,得-b=(2a-c),
化简,得离心率e==2+.
