2022-2023学年九年级数学湘教版上册4.1.1正弦和余弦 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年九年级数学湘教版上册4.1.1正弦和余弦 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 504.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-11 16:43:33 | ||
图片预览







文档简介
(共20张PPT)
想一想:下面实际问题如何解答?
如图,小明沿与地面成65°的山坡从坡底向上走
了90米,那么他上升了多少米?﹝精确到1米﹞
C
A
B
︶
65°
正 弦(1)
1. 通过对实际问题的探索,知道在有一个锐角等
于α的所有直角三角形中,角α的对边与斜边
的比值是一个常数(不变),与直角三角形的
大小无关;
2. 理解掌握锐角的正弦的定义;
3. 能根据锐角的正弦的定义,在直角三角形中
求一个锐角的正弦值.
C
A
B
知识准备
斜边
∠A的对边
1.如图在Rt ABC中, ∠C= 90 , 则AB是___边,
∠A的对边是_____,AC是_______的对边.
∠B的对边
2.两角____________的两个三角形相似.
相似三角形的对应边_________.
斜
BC
∠B
对应相等
成比例
3.在直角三角形中,30 所对的的直角边等于斜边
的_______.
一半
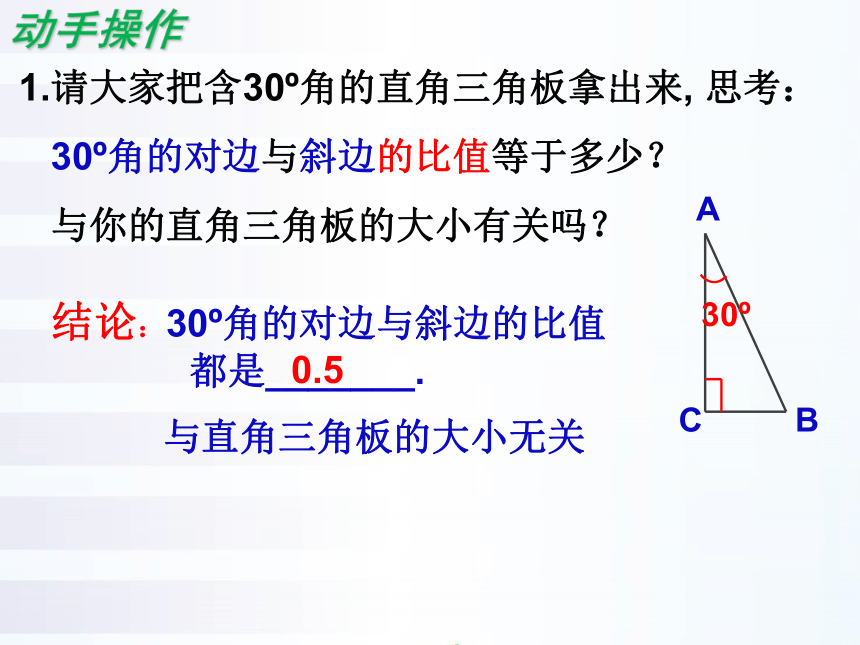
1.请大家把含30 角的直角三角板拿出来, 思考:
30 角的对边与斜边的比值等于多少?
与你的直角三角板的大小有关吗?
结论:30 角的对边与斜边的比值
都是_______.
0.5
A
B
C
动手操作
与直角三角板的大小无关
30
︶
2.每位同学画一个直角三角形,其中一个锐角为
65 ,量出65 角的对边长度和斜边长度,计算:
结论:在有一个锐角为65 的所有直角三角形中,
65 角的对边与斜边的比值是一个常数
(不变),它约等于0.91.
65 角的对边
斜边
=_____(精确到0.01)
思考:
(1)与同桌和邻近桌的同学交流,看看计算出
的比值是否相等?
(2)上面事实说明了什么?
0.91
解:在Rt ABC中,∠A= 65 ,AB=90m,
现在解答下面的问题
如图,小明沿与地面成65°的山坡从坡底向上走了
90米,那么他上升了多少米?﹝精确到1米﹞
C
A
B
︶
65°
∵ =0.91
∴ BC =0.91×90≈82(米)
答:他上升了约82米
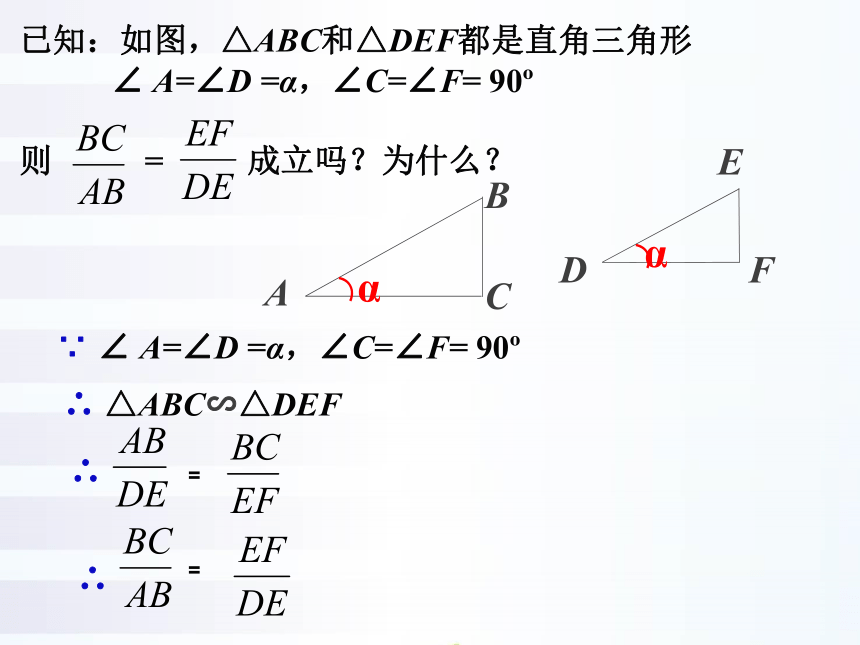
已知:如图,△ABC和△DEF都是直角三角形
∠ A=∠D =α,∠C=∠F= 90
则 = 成立吗?为什么?
3.若把为65 角换成任意一个锐角α,则这个角的
对边和斜边的比值是否也是一个常数(不变)呢?
B
A
C
︶
α
F
E
D
︶
α
已知:如图,△ABC和△DEF都是直角三角形
∠ A=∠D =α,∠C=∠F= 90
则 = 成立吗?为什么?
B
A
C
︶
α
F
E
D
︶
α
∵ ∠ A=∠D =α,∠C=∠F= 90
∴ △ABC∽△DEF
∴
∴
=
=
交流:由上说明了什么?请用语言表达出来.
在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值为一个常数.
→这个比值就叫做角α的正弦
在直角三角形中,锐角α的对边与斜边的比
叫做角α的正弦.
知识方法归纳
B
A
C
︶
α
正弦的定义:
记作:sinα
角α的对边
斜边
即:sinα=
角α的对边
斜边
交流理解:
(1)锐角α的正弦是在______三角形中来定义的
(2)锐角α的正弦就是一个____值,即_________
与_____的比值.
直角
比
角α的对边
斜边
与直角三角形的大小无关。
(3)sinα是一个完整的符号,表示角α的正弦.
(4)sinα表示一个比值,由于直角边小于斜边,
所以0<sinα<1;
(1)求sinA的值;
(2)求sinB的值 .
(1)∠A的对边BC=3,斜边 AB=5
(2)∠B的对边是_____.
C
A
B
3
5
知识方法应用
例1.在Rt ABC中, ∠C= 90 , BC=3,AB=5.
解
∴sinA=
=
AC
根据勾股定理,得
AB 2— BC 2
AC=
5 2— 3 2
=
=4
∴sinB=
=
5
例2.在Rt ABC中,∠C= 90 ,BC=3,AC=5 .
C
A
B
3
(1)求sinA的值;
(2)求sinB的值 .
解
根据勾股定理,得
AB =
AC 2 + BC 2
=
5 2 + 3 2
=
(1)∠A的对边BC=3,
∴sinA=
=
=
(2)∠B的对边AC=5.
∴sinB=
=
=
1.在Rt ABC中,若三边长都扩大3倍,
则锐角A的正弦值( )
A、扩大3倍 B、不变
C、缩小3倍 D、无法确定。
B
自主练习交流
2.如图,在 ABC中, ∠C= 90 , AB=12,
sinA= ,
C
A
B
12
9
则BC的长是______.
3.正方形网格中,△AOB如图放置,则sin∠AOB=( )
A. B.
C. D.
C
4.如图在Rt ABC中, ∠C= 90 , BC= AB
则sinA =_______,sinB=_______.
C
A
B
5.如图,在 ABC中, ∠C= 90 , AC=8,
sinA= ,则BC =____,AB=____.
C
A
B
8
6
10
6.在Rt △ABC 中, ∠C= 90 , BC=5,AB=6.求 , 的值.
6
B
C
A
5
解
AC
∴
=
=
∴
=
=
=
=
课堂小结
通过这节课的学习,你有哪些收获?
作业布置
课本111页练习1,2
想一想:下面实际问题如何解答?
如图,小明沿与地面成65°的山坡从坡底向上走
了90米,那么他上升了多少米?﹝精确到1米﹞
C
A
B
︶
65°
正 弦(1)
1. 通过对实际问题的探索,知道在有一个锐角等
于α的所有直角三角形中,角α的对边与斜边
的比值是一个常数(不变),与直角三角形的
大小无关;
2. 理解掌握锐角的正弦的定义;
3. 能根据锐角的正弦的定义,在直角三角形中
求一个锐角的正弦值.
C
A
B
知识准备
斜边
∠A的对边
1.如图在Rt ABC中, ∠C= 90 , 则AB是___边,
∠A的对边是_____,AC是_______的对边.
∠B的对边
2.两角____________的两个三角形相似.
相似三角形的对应边_________.
斜
BC
∠B
对应相等
成比例
3.在直角三角形中,30 所对的的直角边等于斜边
的_______.
一半
1.请大家把含30 角的直角三角板拿出来, 思考:
30 角的对边与斜边的比值等于多少?
与你的直角三角板的大小有关吗?
结论:30 角的对边与斜边的比值
都是_______.
0.5
A
B
C
动手操作
与直角三角板的大小无关
30
︶
2.每位同学画一个直角三角形,其中一个锐角为
65 ,量出65 角的对边长度和斜边长度,计算:
结论:在有一个锐角为65 的所有直角三角形中,
65 角的对边与斜边的比值是一个常数
(不变),它约等于0.91.
65 角的对边
斜边
=_____(精确到0.01)
思考:
(1)与同桌和邻近桌的同学交流,看看计算出
的比值是否相等?
(2)上面事实说明了什么?
0.91
解:在Rt ABC中,∠A= 65 ,AB=90m,
现在解答下面的问题
如图,小明沿与地面成65°的山坡从坡底向上走了
90米,那么他上升了多少米?﹝精确到1米﹞
C
A
B
︶
65°
∵ =0.91
∴ BC =0.91×90≈82(米)
答:他上升了约82米
已知:如图,△ABC和△DEF都是直角三角形
∠ A=∠D =α,∠C=∠F= 90
则 = 成立吗?为什么?
3.若把为65 角换成任意一个锐角α,则这个角的
对边和斜边的比值是否也是一个常数(不变)呢?
B
A
C
︶
α
F
E
D
︶
α
已知:如图,△ABC和△DEF都是直角三角形
∠ A=∠D =α,∠C=∠F= 90
则 = 成立吗?为什么?
B
A
C
︶
α
F
E
D
︶
α
∵ ∠ A=∠D =α,∠C=∠F= 90
∴ △ABC∽△DEF
∴
∴
=
=
交流:由上说明了什么?请用语言表达出来.
在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值为一个常数.
→这个比值就叫做角α的正弦
在直角三角形中,锐角α的对边与斜边的比
叫做角α的正弦.
知识方法归纳
B
A
C
︶
α
正弦的定义:
记作:sinα
角α的对边
斜边
即:sinα=
角α的对边
斜边
交流理解:
(1)锐角α的正弦是在______三角形中来定义的
(2)锐角α的正弦就是一个____值,即_________
与_____的比值.
直角
比
角α的对边
斜边
与直角三角形的大小无关。
(3)sinα是一个完整的符号,表示角α的正弦.
(4)sinα表示一个比值,由于直角边小于斜边,
所以0<sinα<1;
(1)求sinA的值;
(2)求sinB的值 .
(1)∠A的对边BC=3,斜边 AB=5
(2)∠B的对边是_____.
C
A
B
3
5
知识方法应用
例1.在Rt ABC中, ∠C= 90 , BC=3,AB=5.
解
∴sinA=
=
AC
根据勾股定理,得
AB 2— BC 2
AC=
5 2— 3 2
=
=4
∴sinB=
=
5
例2.在Rt ABC中,∠C= 90 ,BC=3,AC=5 .
C
A
B
3
(1)求sinA的值;
(2)求sinB的值 .
解
根据勾股定理,得
AB =
AC 2 + BC 2
=
5 2 + 3 2
=
(1)∠A的对边BC=3,
∴sinA=
=
=
(2)∠B的对边AC=5.
∴sinB=
=
=
1.在Rt ABC中,若三边长都扩大3倍,
则锐角A的正弦值( )
A、扩大3倍 B、不变
C、缩小3倍 D、无法确定。
B
自主练习交流
2.如图,在 ABC中, ∠C= 90 , AB=12,
sinA= ,
C
A
B
12
9
则BC的长是______.
3.正方形网格中,△AOB如图放置,则sin∠AOB=( )
A. B.
C. D.
C
4.如图在Rt ABC中, ∠C= 90 , BC= AB
则sinA =_______,sinB=_______.
C
A
B
5.如图,在 ABC中, ∠C= 90 , AC=8,
sinA= ,则BC =____,AB=____.
C
A
B
8
6
10
6.在Rt △ABC 中, ∠C= 90 , BC=5,AB=6.求 , 的值.
6
B
C
A
5
解
AC
∴
=
=
∴
=
=
=
=
课堂小结
通过这节课的学习,你有哪些收获?
作业布置
课本111页练习1,2
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
