镶嵌[下学期]
图片预览




文档简介
(共41张PPT)
§7.4 镶嵌
人教版七年级下册第七章
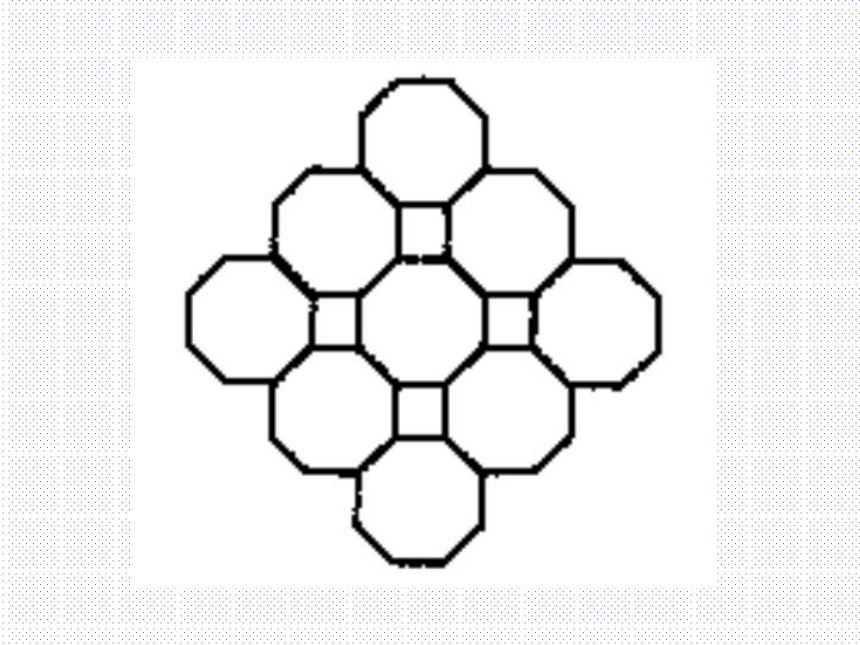
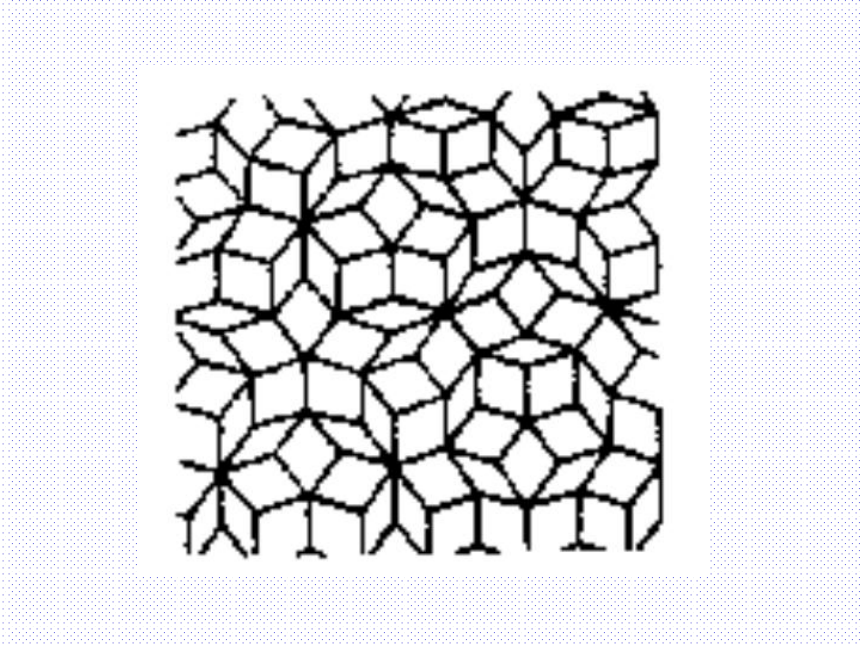
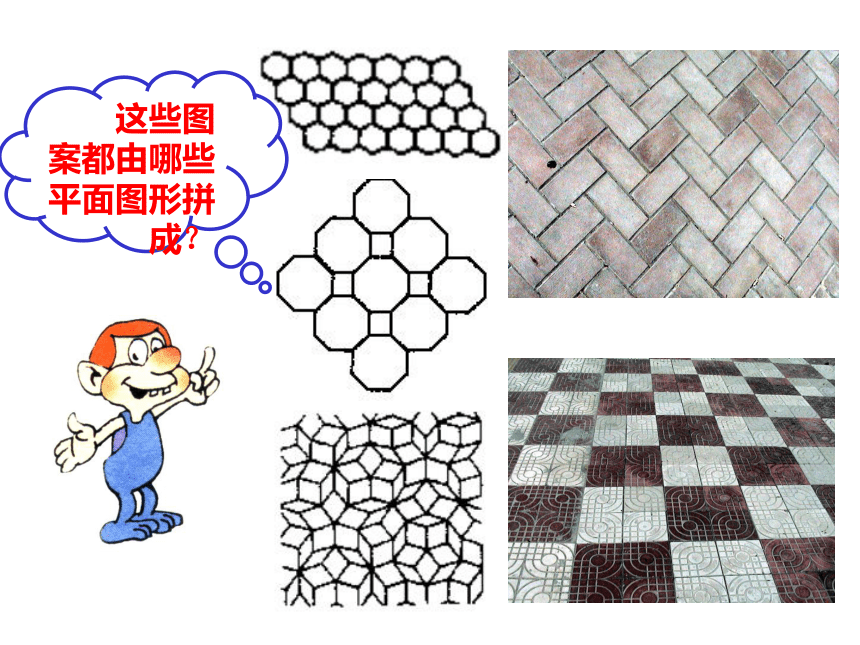
这些图案都由哪些平面图形拼成?
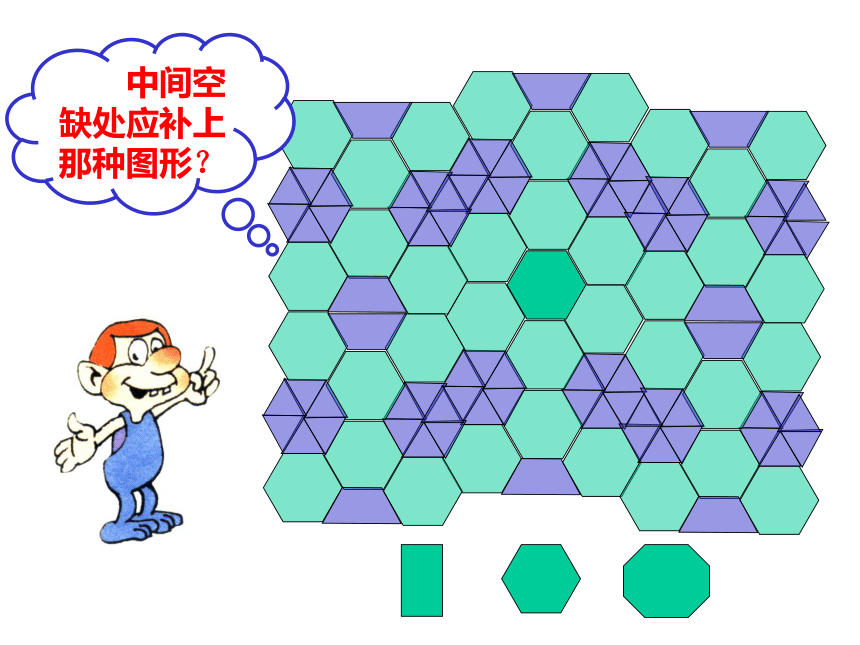
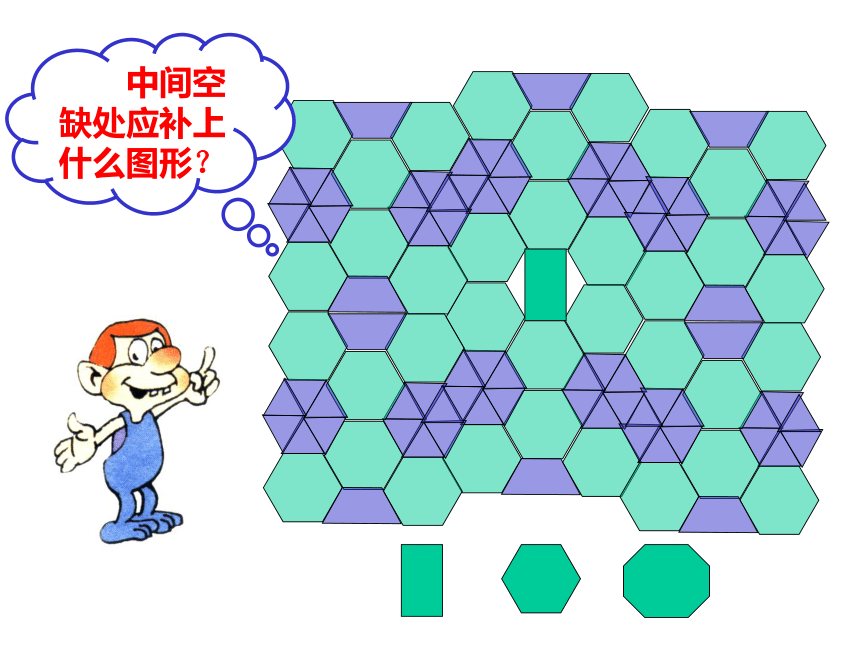
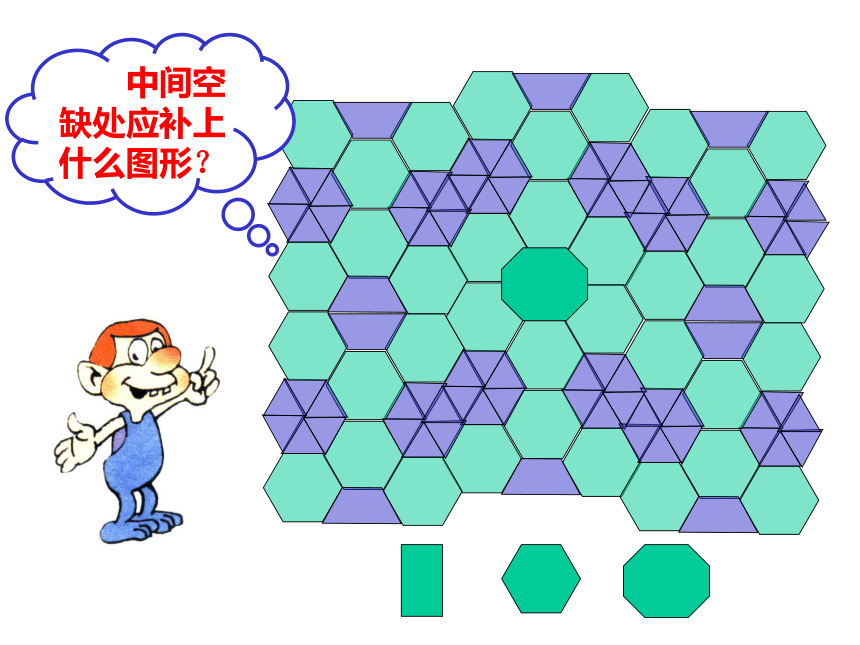
中间空缺处应补上那种图形?
中间空缺处应补上什么图形?
中间空缺处应补上什么图形?
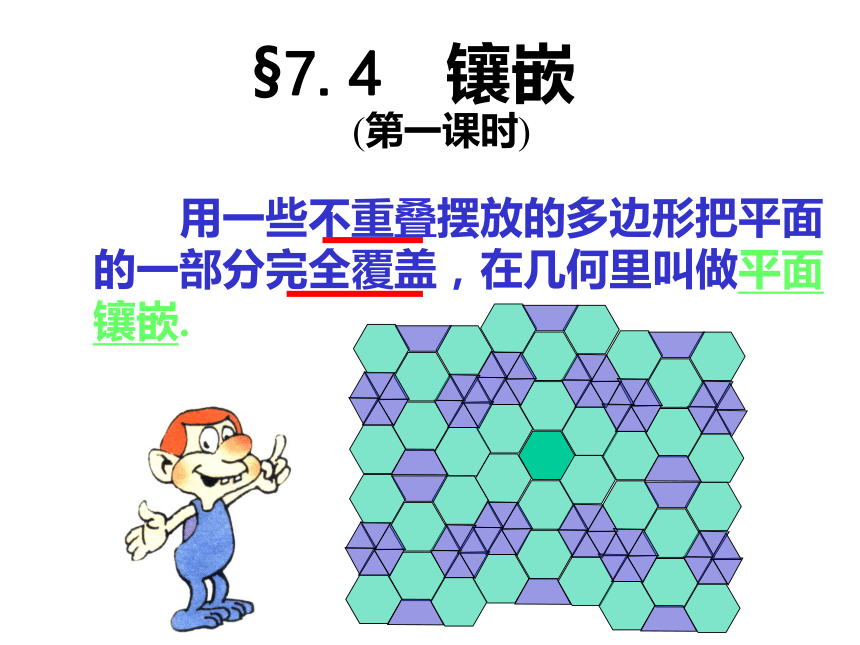
用一些不重叠摆放的多边形把平面的一部分完全覆盖,在几何里叫做平面镶嵌.
§7.4 镶嵌
(第一课时)
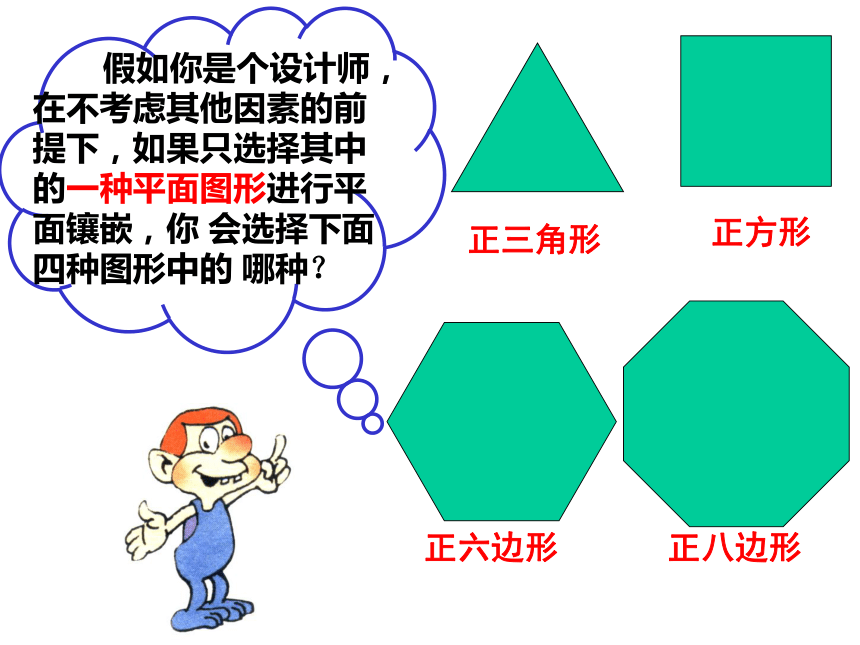
假如你是个设计师, 在不考虑其他因素的前提下,如果只选择其中的一种平面图形进行平面镶嵌,你 会选择下面四种图形中的 哪种?
正三角形
正方形
正六边形
正八边形
拼拼看
拼拼看
拼拼看
拼拼看
拼拼看
为什么有的正多边形可以镶嵌,而有的却不能镶嵌?
议一议
理一理
6
60
0
90
0
135
0
120
0
4
3
2
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
135 ×2<360
0
0
135 ×3>360
0
0
120 ×3=360
0
0
不能拼好
有重叠
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =8
n = 6
议一议
一种正多边形能进行镶嵌应满足什么条件?
不能拼好
有重叠
6
60
0
90
0
135
0
120
0
4
3
2
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
135 ×2<360
0
0
135 ×3>360
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =8
n = 6
0
当这种正多边形的每个内角的度数恰好是360 的约数时,这种正多边形就能镶嵌.
0
规律:
练一练
1. 仅用正十边形能进行镶嵌吗
为什么
2. 只用一种正多边形能进行镶嵌的有
_____________________.
正三角形、正方形、 正六边形
如果选择其中的两种平面图形进行镶嵌,你又会选择哪两种呢 ?
正三角形
正方形
想一想
正六边形
正八边形
拼拼看
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.
规律:
用三种或多种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的几种正多边形的内角加在一起恰好组成一个周角时,这几种正多边形就能镶嵌.
这是某公园的呈正六边形的花坛,现要在其周围用正多边形铺地,请你设计出一种铺法,并画出草图?
请你创造美
欢迎指正
拼拼看
拼拼看
拼拼看
拼拼看
拼拼看
欣赏不同的组合方式:
练习
1、小颖家购买了一套新房,准备用一种地板砖镶嵌新居地面,要求地板砖都是正多边形,且每块地板砖的各边长都相等,各个角也相等。某家装饰材料市场有如下五种型号的正多边形地板砖,他们每个角的度数分别是60°,90°。108°,120°,135°,你认为这些地板砖那些适用?
若允许可用多种,则有哪些不同的组合方式?
2、在下图中,所示的正多边形中用同一种图形不能做平面镶嵌的是( )
B
A
C
D
§7.4 镶嵌
人教版七年级下册第七章
这些图案都由哪些平面图形拼成?
中间空缺处应补上那种图形?
中间空缺处应补上什么图形?
中间空缺处应补上什么图形?
用一些不重叠摆放的多边形把平面的一部分完全覆盖,在几何里叫做平面镶嵌.
§7.4 镶嵌
(第一课时)
假如你是个设计师, 在不考虑其他因素的前提下,如果只选择其中的一种平面图形进行平面镶嵌,你 会选择下面四种图形中的 哪种?
正三角形
正方形
正六边形
正八边形
拼拼看
拼拼看
拼拼看
拼拼看
拼拼看
为什么有的正多边形可以镶嵌,而有的却不能镶嵌?
议一议
理一理
6
60
0
90
0
135
0
120
0
4
3
2
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
135 ×2<360
0
0
135 ×3>360
0
0
120 ×3=360
0
0
不能拼好
有重叠
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =8
n = 6
议一议
一种正多边形能进行镶嵌应满足什么条件?
不能拼好
有重叠
6
60
0
90
0
135
0
120
0
4
3
2
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
135 ×2<360
0
0
135 ×3>360
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =8
n = 6
0
当这种正多边形的每个内角的度数恰好是360 的约数时,这种正多边形就能镶嵌.
0
规律:
练一练
1. 仅用正十边形能进行镶嵌吗
为什么
2. 只用一种正多边形能进行镶嵌的有
_____________________.
正三角形、正方形、 正六边形
如果选择其中的两种平面图形进行镶嵌,你又会选择哪两种呢 ?
正三角形
正方形
想一想
正六边形
正八边形
拼拼看
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角加在一起恰好组成一个周角时,这两种正多边形就能镶嵌.
规律:
用三种或多种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的几种正多边形的内角加在一起恰好组成一个周角时,这几种正多边形就能镶嵌.
这是某公园的呈正六边形的花坛,现要在其周围用正多边形铺地,请你设计出一种铺法,并画出草图?
请你创造美
欢迎指正
拼拼看
拼拼看
拼拼看
拼拼看
拼拼看
欣赏不同的组合方式:
练习
1、小颖家购买了一套新房,准备用一种地板砖镶嵌新居地面,要求地板砖都是正多边形,且每块地板砖的各边长都相等,各个角也相等。某家装饰材料市场有如下五种型号的正多边形地板砖,他们每个角的度数分别是60°,90°。108°,120°,135°,你认为这些地板砖那些适用?
若允许可用多种,则有哪些不同的组合方式?
2、在下图中,所示的正多边形中用同一种图形不能做平面镶嵌的是( )
B
A
C
D
