7.1课题学习--镶嵌[下学期]
文档属性
| 名称 | 7.1课题学习--镶嵌[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-25 08:56:00 | ||
图片预览






文档简介
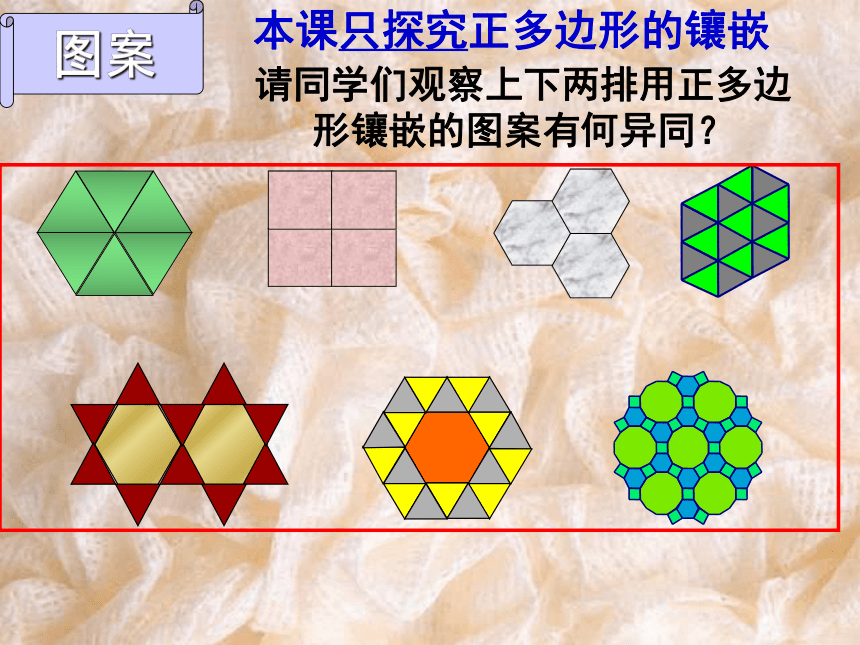
课件29张PPT。课题学习:镶嵌人教版七年级(下)7.4 课题学习 镶嵌欣赏图案问题(1)这些图案都是由哪些基本的平面图形
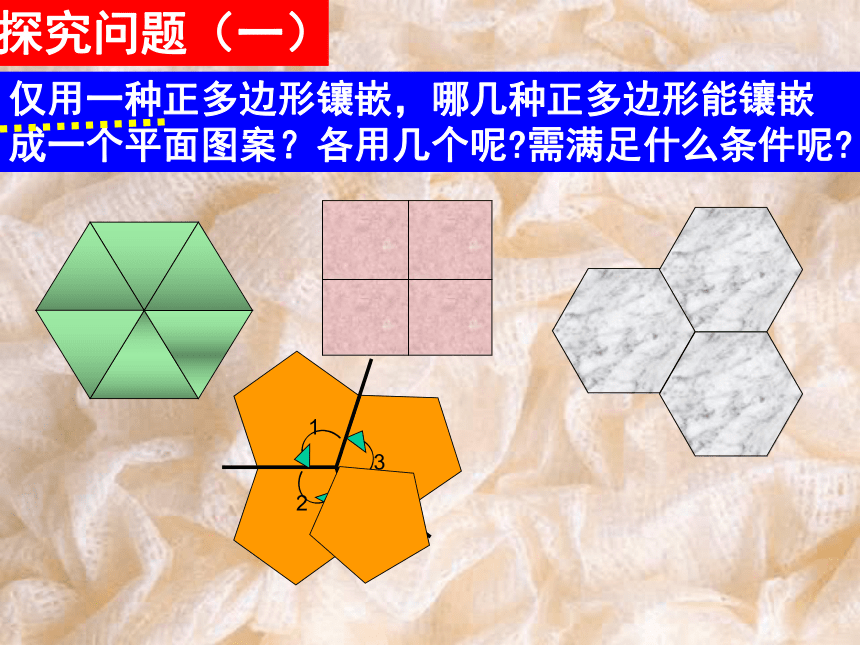
构成的?(2)这些图形拼成一个平面的共同特征是什么?镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。图案本课只探究正多边形的镶嵌请同学们观察上下两排用正多边形镶嵌的图案有何异同?探究问题(一)仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图案?各用几个呢?需满足什么条件呢?60°K=6能拼好90°K=4能拼好108°K=3不能拼好
有缺口108°K=4不能拼好
有重叠120°K=3能拼好 观察并指出在每个图案中,正多边形必须
具备下列条件:
1)边长_____,
2)顶点______,
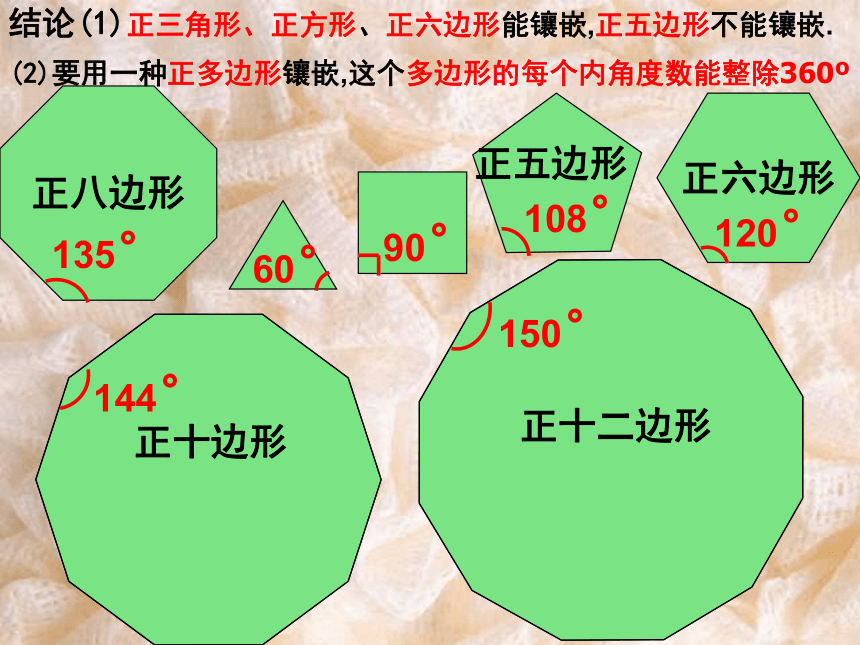
3)在一个顶点处_________________________相等公用各多边形的内角之和为360度仅用一种正多边形镶嵌,只有正三角形、正方形、正六边形能镶嵌成一个平面吗?正六边形正八边形正十边形正十二边形正五边形结论(1)正三角形、正方形、正六边形能镶嵌,正五边形不能镶嵌.(2)要用一种正多边形镶嵌,这个多边形的每个内角度数能整除360o做一做(1)任意剪出一些形状、大小完全相同的三角形纸板,拼拼看,它们能否镶嵌成平面图案. 在镶嵌过程中,请大家观察讨论:每个拼接点处有几个角?它们与这种三角形的三个内角有什么关系?任意全等的三角形能镶嵌,在每个拼接点处有六个角,
而这六个角和恰好是这个三角形的内角和的两倍,
也就是它们的和为360o,且相等的边互相重合。
任意全等的四边形可以镶嵌,在每个拼接点处有四个角,而这四个角的和恰好是这个四边形的四个内角的和,它们的和为360o。且相等的边互相重合。
做一做(2)任意剪出一些形状、大小完全相同的四边形纸板,
拼拼看,它们能否镶嵌成平面图案.
在镶嵌过程中,请大家观察讨论:每个拼接点处的四个角与这种四边形的四个内角有什么关系?能镶嵌的图形在一个拼接点处有什么特点? 几个图形的内角拼接在一起时,其和等于360o,并使相等的边互相重合。
议一议单独用三角形、四边形和正六边形可以镶嵌。哪些单独的图形能镶嵌?问题情景:小明家要装潢了,他的房间要自己设计,地板想用两种正多边形来镶嵌,帮忙设计一个方案吧?
再创情景 拓展探究 用两种正多边形镶嵌,哪些能镶嵌成一个平面?各用几个呢?需要满足什么条件呢?探究问题(二)正六边形正八边形正十边形正十二边形正五边形“先拿大的,小的填空” 用边长相等的正三角形和正方形能不能镶嵌?试一试试一试用边长相等的正三角形和正六边形能不能镶嵌呢?正六边形正六边形正六边形试一试 用边长相等的正方形和正八边形能不能镶嵌呢?3×60°+2× 90°= 360°2×60°+2 ×120°= 360°
4×60°+120°= 360°当围绕一点拼在一起的几个正多边形
的内角加在一起恰好组成一个周角时,
就拼成一个平面图形哪种漂亮些?1)正三角形与正方形镶嵌(4 3 4 3 3)(3 3 3 4 4)图案设计2)正三角形与正六边形镶嵌(3 3 3 3 6)(3 6 3 6)图案设计4)正四边形
与正八边形5)正三角形与
正十二边形3)正五边形
与正十边形(5 5 10)(4 8 8)(12 12 3)图案设计哪种漂亮些?图案设计图案设计漂亮的镶嵌图案埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。他是一个将艺术与数学融合的画家,也因此享誉世界。
???资 料 欣 赏埃舍尔镶嵌艺术作品对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?畅所欲言请你为小明的地板设计一种美丽的图案吧!请你在成长记录册中谈一谈自己的体会吧!用三种正多边形镶嵌,哪些能镶嵌成一个平面?
哪种漂亮些?作业:请各位老师多提宝贵意见,谢谢!
构成的?(2)这些图形拼成一个平面的共同特征是什么?镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。图案本课只探究正多边形的镶嵌请同学们观察上下两排用正多边形镶嵌的图案有何异同?探究问题(一)仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图案?各用几个呢?需满足什么条件呢?60°K=6能拼好90°K=4能拼好108°K=3不能拼好
有缺口108°K=4不能拼好
有重叠120°K=3能拼好 观察并指出在每个图案中,正多边形必须
具备下列条件:
1)边长_____,
2)顶点______,
3)在一个顶点处_________________________相等公用各多边形的内角之和为360度仅用一种正多边形镶嵌,只有正三角形、正方形、正六边形能镶嵌成一个平面吗?正六边形正八边形正十边形正十二边形正五边形结论(1)正三角形、正方形、正六边形能镶嵌,正五边形不能镶嵌.(2)要用一种正多边形镶嵌,这个多边形的每个内角度数能整除360o做一做(1)任意剪出一些形状、大小完全相同的三角形纸板,拼拼看,它们能否镶嵌成平面图案. 在镶嵌过程中,请大家观察讨论:每个拼接点处有几个角?它们与这种三角形的三个内角有什么关系?任意全等的三角形能镶嵌,在每个拼接点处有六个角,
而这六个角和恰好是这个三角形的内角和的两倍,
也就是它们的和为360o,且相等的边互相重合。
任意全等的四边形可以镶嵌,在每个拼接点处有四个角,而这四个角的和恰好是这个四边形的四个内角的和,它们的和为360o。且相等的边互相重合。
做一做(2)任意剪出一些形状、大小完全相同的四边形纸板,
拼拼看,它们能否镶嵌成平面图案.
在镶嵌过程中,请大家观察讨论:每个拼接点处的四个角与这种四边形的四个内角有什么关系?能镶嵌的图形在一个拼接点处有什么特点? 几个图形的内角拼接在一起时,其和等于360o,并使相等的边互相重合。
议一议单独用三角形、四边形和正六边形可以镶嵌。哪些单独的图形能镶嵌?问题情景:小明家要装潢了,他的房间要自己设计,地板想用两种正多边形来镶嵌,帮忙设计一个方案吧?
再创情景 拓展探究 用两种正多边形镶嵌,哪些能镶嵌成一个平面?各用几个呢?需要满足什么条件呢?探究问题(二)正六边形正八边形正十边形正十二边形正五边形“先拿大的,小的填空” 用边长相等的正三角形和正方形能不能镶嵌?试一试试一试用边长相等的正三角形和正六边形能不能镶嵌呢?正六边形正六边形正六边形试一试 用边长相等的正方形和正八边形能不能镶嵌呢?3×60°+2× 90°= 360°2×60°+2 ×120°= 360°
4×60°+120°= 360°当围绕一点拼在一起的几个正多边形
的内角加在一起恰好组成一个周角时,
就拼成一个平面图形哪种漂亮些?1)正三角形与正方形镶嵌(4 3 4 3 3)(3 3 3 4 4)图案设计2)正三角形与正六边形镶嵌(3 3 3 3 6)(3 6 3 6)图案设计4)正四边形
与正八边形5)正三角形与
正十二边形3)正五边形
与正十边形(5 5 10)(4 8 8)(12 12 3)图案设计哪种漂亮些?图案设计图案设计漂亮的镶嵌图案埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。他是一个将艺术与数学融合的画家,也因此享誉世界。
???资 料 欣 赏埃舍尔镶嵌艺术作品对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?畅所欲言请你为小明的地板设计一种美丽的图案吧!请你在成长记录册中谈一谈自己的体会吧!用三种正多边形镶嵌,哪些能镶嵌成一个平面?
哪种漂亮些?作业:请各位老师多提宝贵意见,谢谢!
