镶嵌[下学期]

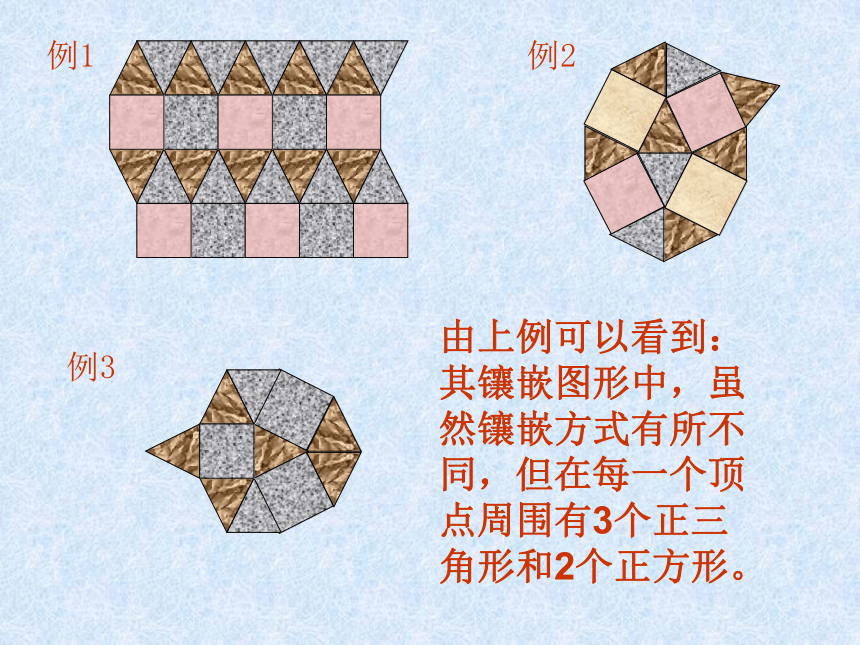
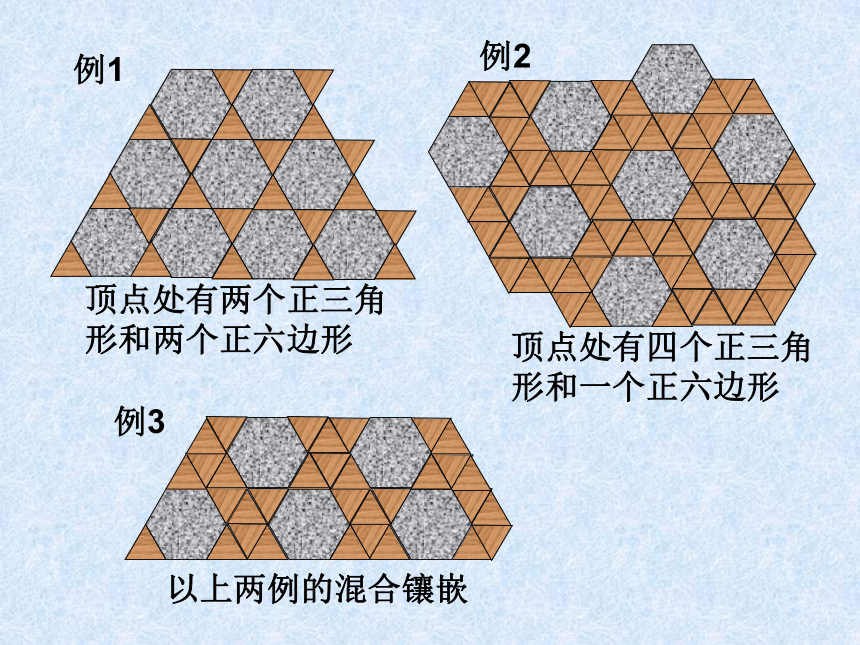
课件12张PPT。7.19 探究性活动镶嵌孝感市文昌中学 程世富（二）要设计几种地板图案，必须解决如下问题：1. 如果限于用一种正多边形镶嵌,哪几种多边形能镶嵌成一个平面?2. 如果允许用几种正多边形组合起来镶嵌,由哪几种多边形组合起来能镶嵌成一个平面?这种情况上次课已经讨论下面研究这种情况分别讨论如下：(1)正三角形与正方形因此这样的平面镶嵌存在。(一)用两种正多边形镶嵌：设在一个顶点周围有m个正三角形的角、n个正方形的角。那么这些角的和应满足方程：m·60°+n·90°=360°即：2m+3n=12这个方程的整数解为：想一想，在它的每一个顶点周围有几个正三角形和几个正方形。由计算知：一个顶点周围有3个正三角形和2个正方形。其镶嵌图形如下例：例1例2例3由上例可以看到：其镶嵌图形中，虽然镶嵌方式有所不同，但在每一个顶点周围有3个正三角形和2个正方形。(2)正三角形与正六边形因此这样的平面镶嵌存在。设在一个顶点周围有m个正三角形的角、n个正六边形的角。那么这些角的和应满足方程：m·60°+n·120°=360°即：m+2n=6这个方程的整数解为：想一想，在它的每一个顶点周围有几个正三角形和几个正方形。由计算知：一个顶点周围有4个正三角形和1个正六边形或有2个正三角形和2个正六边形。其镶嵌图形如下例：或顶点处有两个正三角形和两个正六边形顶点处有四个正三角形和一个正六边形以上两例的混合镶嵌例1例2例3想一想:1、如果用正三角形与正十二边形作平面镶嵌，有几种可能的情况？为什么？设在一个顶点周围有m个正三角形的角、n个正十二边形的角。那么这些角的和应满足方程：m·60°+n·150°=360°即：2m+5n=12这个方程的整数解为：1、如果用正四边形与正八边形作平面镶嵌，有几种可能的情况？为什么？(二)假如用三种不同的正多边形镶嵌，同样，必须在一个顶点处，正多边形的内角之和为360°，如果正多边形的边数分别为n1、n2、n3，且每一个顶点处一种正多边形只有一个，则根据平面镶嵌的条件，必须有：++=360°∴∴∴上式的正整数解见下表：此镶嵌为表中一例由以上分析和讨论可知： 正多边形的镶嵌问题，是丰富多采的，对于四种以及以上情况，同学们可以仿照上面的方法自己去研究。 此外，一般的凸多边形（不是正多边形），有的也能用来作为平面镶嵌。再见