课题学习:镶嵌[下学期]
文档属性
| 名称 | 课题学习:镶嵌[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 928.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-27 00:00:00 | ||
图片预览








文档简介
课件50张PPT。小 结 S h u x u e台州市书生中学朱仁江制作美妙的镶嵌学海中学初一备课组埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。他是一个将艺术与数学融合的画家,也因此享誉世界。
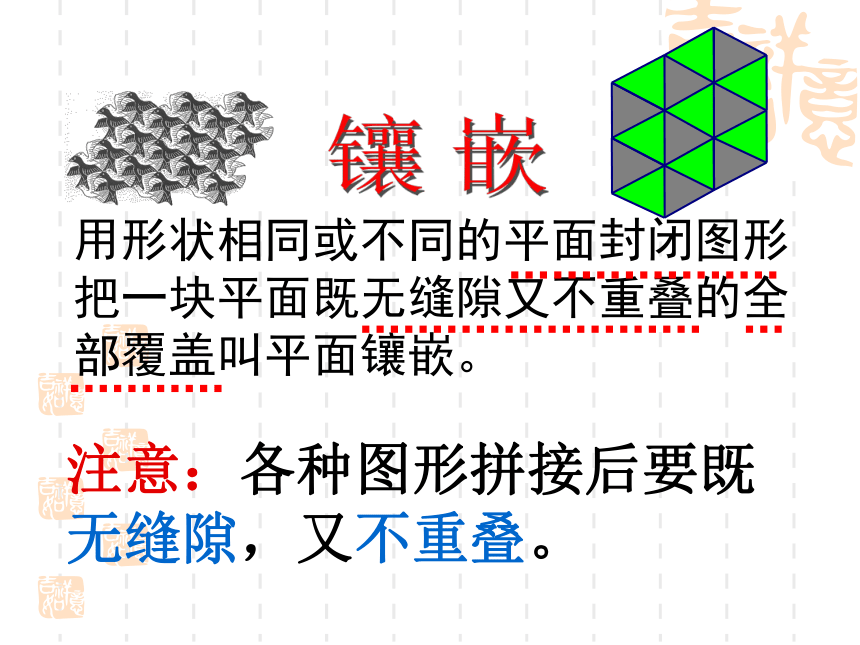
???资 料埃舍尔的作品欣 赏镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。注意:各种图形拼接后要既无缝隙,又不重叠。请你帮忙:小新搬新家了,他的房间要自己设计,地板想用一种正多边形的瓷砖来镶嵌,商店有以下几种瓷砖出售,请帮小新选一种。
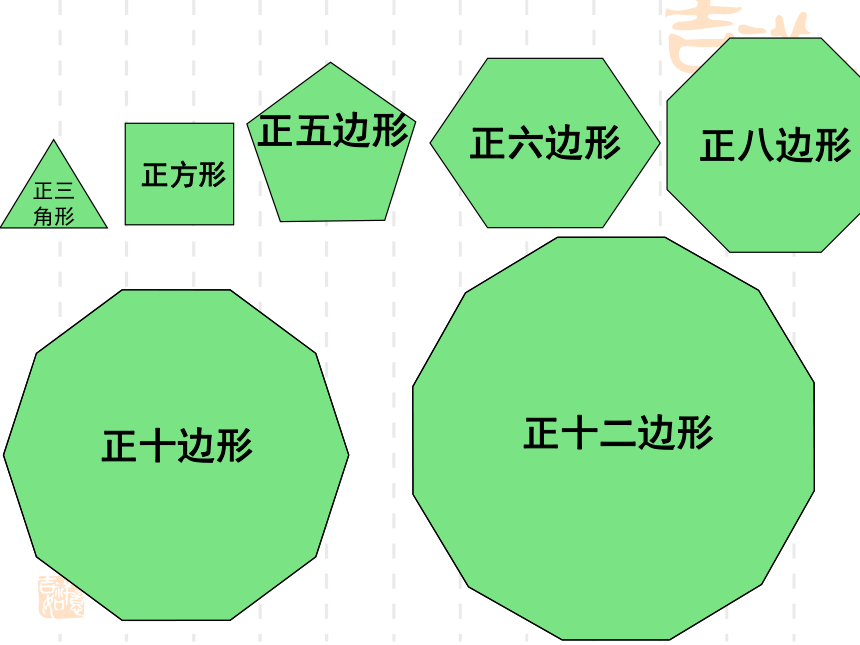
正六边形正八边形正十边形正十二边形正五边形正方形正三
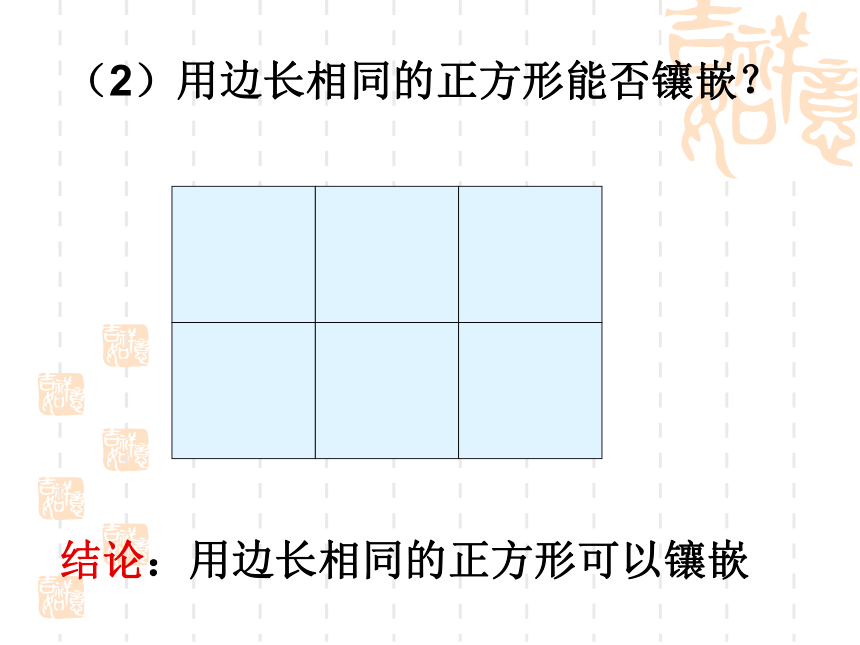
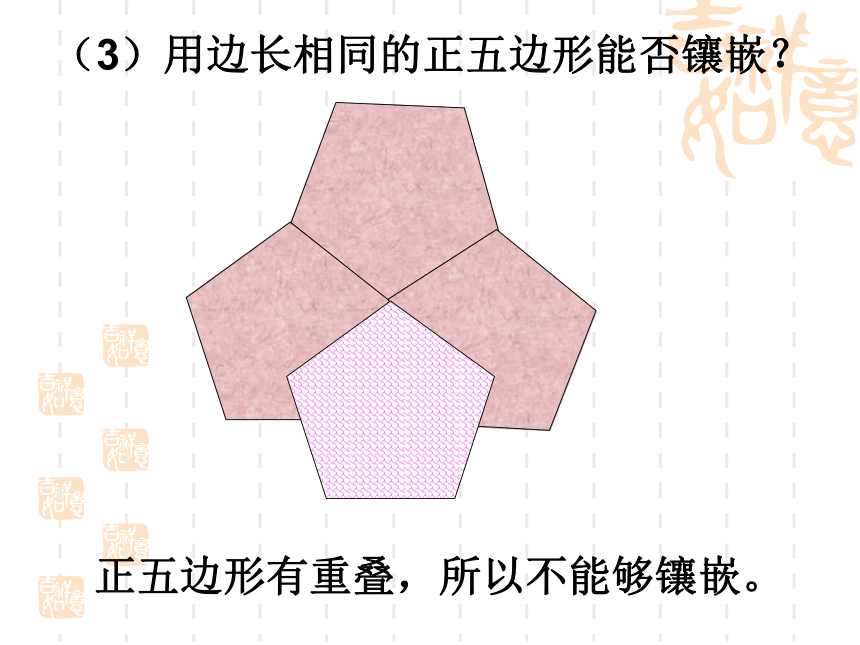
角形做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌正五边形有重叠,所以不能够镶嵌。(3)用边长相同的正五边形能否镶嵌?啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌八边形有重叠,所以不能够镶嵌。结论要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度”仅用一种正多边形镶嵌,
只有正三角形、正方形、正六边形
能镶嵌成一个平面。结论:思考:如果是任意的多边形,又有哪些能镶嵌呢?只有三角形和四边形。请同学们剪一些全等的四边形纸片,将它们多次旋转和平移,就拼成了一幅镶嵌图,你知道为什么吗?1 关注数学中的美 2 关注身边的数学随堂启迪问题用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?∴2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角
的角,n 个正方形的角,则有
∵ m,n 为正整数∴解为∴m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,
n 个正六边形的角,则有∵ m,n 为正整数∴解为∴2 m+3 n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,
n 个正八边形的角,则有∵ m,n 为正整数∴解为设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有∴3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解为正三角形与正十二边形用三种正多边形镶嵌,哪些能镶嵌成一个平面?探究问题(三)1、正六边形、正方形和正三角形的组合。2、正十二边形、正六边形和正方形的组合。 1 、平面镶嵌的定义
2 、镶嵌的意义、条件、作用、方法
3 、关注身边的数学
4 、关注数学中的美总结:课堂小结 本节课我们通过活动,探讨,知道任意一个三角形,四边形或正六边形可以镶嵌成一个平面,并且探索出正多边形镶嵌的条件.即:一种正多边形的一个内角的倍数是否是360°
作业: 请同学搜集一些平面镶嵌图案,用硬纸片做出其中的一二个模型.利用镶嵌可以得到一些绚丽多彩的图案
???资 料埃舍尔的作品欣 赏镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。注意:各种图形拼接后要既无缝隙,又不重叠。请你帮忙:小新搬新家了,他的房间要自己设计,地板想用一种正多边形的瓷砖来镶嵌,商店有以下几种瓷砖出售,请帮小新选一种。
正六边形正八边形正十边形正十二边形正五边形正方形正三
角形做一做 (1)用边长相同的正三角形能否镶嵌?结论:用边长相同的正三角形可以镶嵌(2)用边长相同的正方形能否镶嵌?结论:用边长相同的正方形可以镶嵌正五边形有重叠,所以不能够镶嵌。(3)用边长相同的正五边形能否镶嵌?啊!拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=?(4)用边长相同的正六边形能否镶嵌?结论:用边长相同的正六边形可以镶嵌八边形有重叠,所以不能够镶嵌。结论要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.正六边形正八边形正十边形正十二边形正五边形“内角必须整除360度”仅用一种正多边形镶嵌,
只有正三角形、正方形、正六边形
能镶嵌成一个平面。结论:思考:如果是任意的多边形,又有哪些能镶嵌呢?只有三角形和四边形。请同学们剪一些全等的四边形纸片,将它们多次旋转和平移,就拼成了一幅镶嵌图,你知道为什么吗?1 关注数学中的美 2 关注身边的数学随堂启迪问题用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?∴2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角
的角,n 个正方形的角,则有
∵ m,n 为正整数∴解为∴m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,
n 个正六边形的角,则有∵ m,n 为正整数∴解为∴2 m+3 n=8m=1
n=2设在一个顶点周围有个 m 正四边形的角,
n 个正八边形的角,则有∵ m,n 为正整数∴解为设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有∴3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解为正三角形与正十二边形用三种正多边形镶嵌,哪些能镶嵌成一个平面?探究问题(三)1、正六边形、正方形和正三角形的组合。2、正十二边形、正六边形和正方形的组合。 1 、平面镶嵌的定义
2 、镶嵌的意义、条件、作用、方法
3 、关注身边的数学
4 、关注数学中的美总结:课堂小结 本节课我们通过活动,探讨,知道任意一个三角形,四边形或正六边形可以镶嵌成一个平面,并且探索出正多边形镶嵌的条件.即:一种正多边形的一个内角的倍数是否是360°
作业: 请同学搜集一些平面镶嵌图案,用硬纸片做出其中的一二个模型.利用镶嵌可以得到一些绚丽多彩的图案
