镶嵌[下学期]
图片预览










文档简介
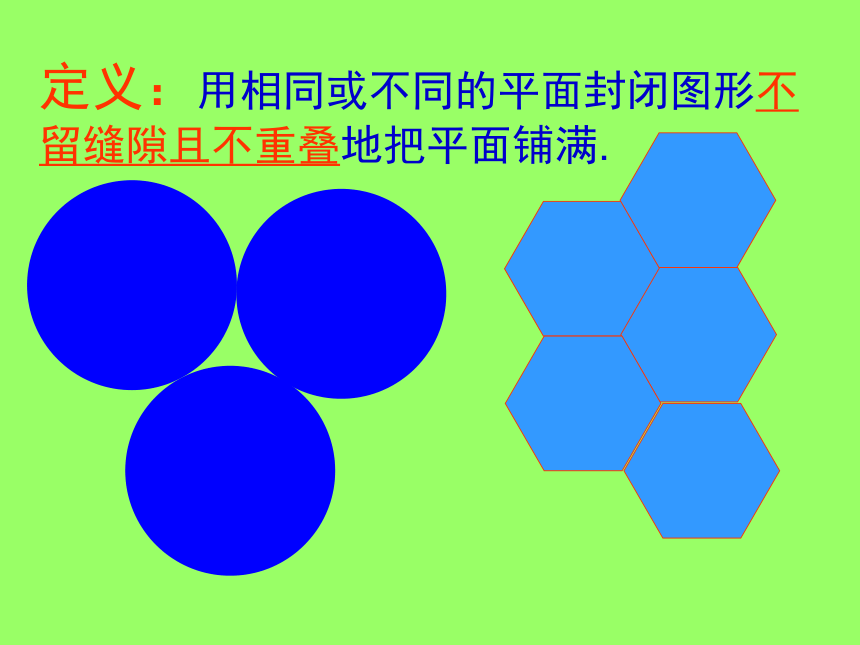
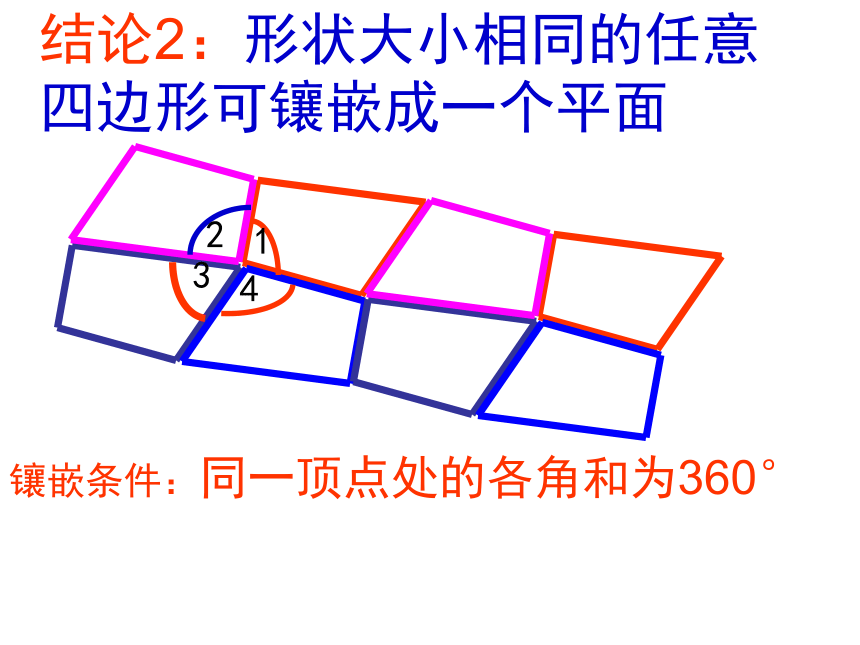
课件37张PPT。镶嵌 面 平 泽国三中定义:用相同或不同的平面封闭图形不留缝隙且不重叠地把平面铺满.形状大小相同的任意三角形能镶嵌 成一个平面 ? .结论1:形状大小相同的任意三角形可镶嵌 成一个平面 .原因:交点处角度之和为360°研究四边形结论2:形状大小相同的任意四边形可镶嵌成一个平面1234镶嵌条件:同一顶点处的各角和为360°问题1:只用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?√〤√√〤〤观察图形6个4个3个108o135o36o90o? m = 360°(n-2) (m-2) =4=1X4=2X2=4X1结论:只用一种正多边形,只有正3,4,6边形能镶嵌成 一个平面.n= 4
m= 4n= 6
m= 3探究原因问题2:用两种正多边形组合来镶嵌,哪两种正多边形组合起来能镶嵌成一个平面?1.由正三角形与正方形m?60°+n ?90°=360°
2m+3n=12
m=3, n=2结论:一个顶点处3个正三角形和2个正方形可镶嵌平面2.由正三角形与正六边形m?60°+n ?120°=360°
m+2n=6
m=4, n=1或 m=2, n=2结论: 一个顶点处4个正三角形和1个正六边形或
一个顶点处2个正三角形和2个正六边形可镶嵌平面请 看 图 案3.由正三角形与正十二边形m?60°+n ?150°=360°
2m+5n=12
m=1, n=24.由正方形与正八边形m?90°+n ?135°=360°
2m+3n=8
m=1, n=25.由正方形与正六边形m?90°+n ?120°=360°
3m+4n=12
方程无正整数解,无法镶嵌研究方法:用代数方程研究几何图形关系6.由正五边形与正六边形问题3:用三种正多边形镶嵌,哪几种正多边形组合起来能镶嵌成一个平面?设三种正多边形分边数分别为x,y,z++=360++=请欣赏让我们学会欣赏美 更学会用数学去创造美
泽国三中
2006年3月
m= 4n= 6
m= 3探究原因问题2:用两种正多边形组合来镶嵌,哪两种正多边形组合起来能镶嵌成一个平面?1.由正三角形与正方形m?60°+n ?90°=360°
2m+3n=12
m=3, n=2结论:一个顶点处3个正三角形和2个正方形可镶嵌平面2.由正三角形与正六边形m?60°+n ?120°=360°
m+2n=6
m=4, n=1或 m=2, n=2结论: 一个顶点处4个正三角形和1个正六边形或
一个顶点处2个正三角形和2个正六边形可镶嵌平面请 看 图 案3.由正三角形与正十二边形m?60°+n ?150°=360°
2m+5n=12
m=1, n=24.由正方形与正八边形m?90°+n ?135°=360°
2m+3n=8
m=1, n=25.由正方形与正六边形m?90°+n ?120°=360°
3m+4n=12
方程无正整数解,无法镶嵌研究方法:用代数方程研究几何图形关系6.由正五边形与正六边形问题3:用三种正多边形镶嵌,哪几种正多边形组合起来能镶嵌成一个平面?设三种正多边形分边数分别为x,y,z++=360++=请欣赏让我们学会欣赏美 更学会用数学去创造美
泽国三中
2006年3月
