2.5 角平分线 课件

课件12张PPT。请你帮帮它如图，两条小河交汇形成的三角区，土壤肥沃，气候宜人，小猪看中了这块宝地，想在这里建一个小房子，并使房子到两条小河的距离相等，但它不知该如何选址，你能帮帮它吗？ 房子该建在哪儿呢？2.5 角平分线的性质复习回顾 1、角是轴对称图形吗？它有几条对称轴？什么叫做角平分线？2、角平分线有什么性质？（1）角平分线上的点到角两边的距离相等。PPD⊥OA，PE⊥OB∵ OC是∠AOB的平分线∴ PD＝PE用数学语言表述：你能证明吗？角的平分线上的点到角的两边的距离相等。已知OP平分∠ＡＯＢ，PD⊥OA,PE⊥OB垂足分别为D、E。
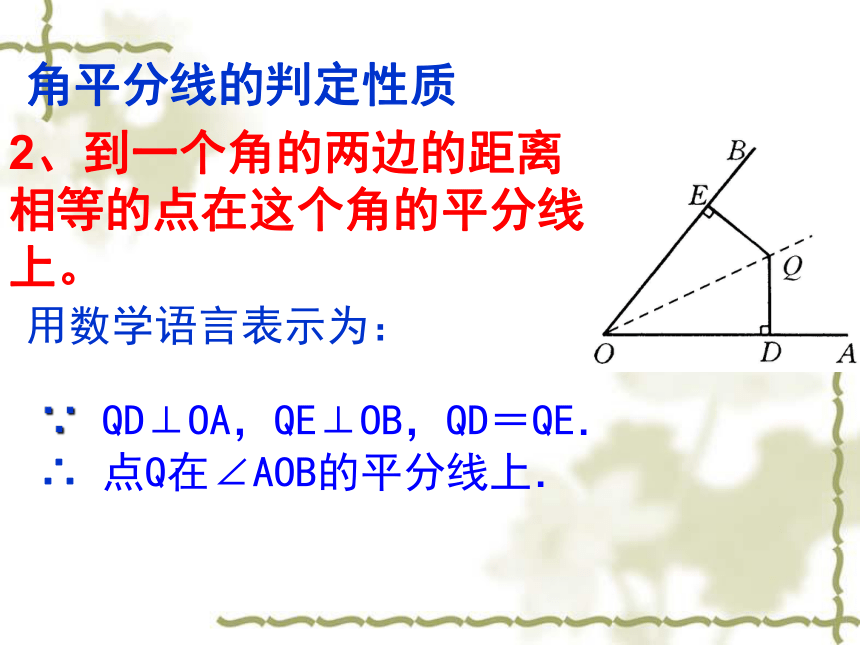
求证：PD＝PE。2、到一个角的两边的距离相等的点在这个角的平分线上。∵ QD⊥OA，QE⊥OB，QD＝QE．
∴ 点Q在∠AOB的平分线上．用数学语言表示为：角平分线的判定性质1、如图, △ABC的角平分线BM,CN相交于点P,求证：点P也在∠BAC的平分线上.∵BM是△ABC的角平分线,点P在BM上, PD⊥AB， PE⊥BC∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PF.证明：过点P作PD⊥AB于D，PE⊥BC于E，PF⊥AC于F∴点P在∠BAC的平分线上.试一试通过本题的证明，你能得到一个关于三角形角平分线的什么结论？三角形的三条角平分线交于一点，并且交点到三角形三边的距离相等。想一想2、如图，已知△ABC的外角∠CBD和∠BCE的平分线相交于点F，
求证：点F在∠DAE的平分线上．
证明：过点F作FG⊥AE于G，FH⊥AD于H，FM⊥BC于MGHM∵点F在∠BCE的平分线上， 　　　　FG⊥AE， FM⊥BC∴FG＝FM又∵点F在∠CBD的平分线上， 　　　　FH⊥AD， FM⊥BC∴FM＝FH∴FG＝FH∴点F在∠DAE的平分线上　　　巩固运用实践应用1、如图，为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
拓展与延伸2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处D1、关于三角形的角平分线的说法错误的是( )
A.两角平分线的交点在三角形内
B.两角平分线的交点在第三个角的平分线上
C.两角平分线的交点到三边的距离相等
D.两角平分线的交点到三个顶点的距离相等
2、如图，已知△ABC中，∠C=90°，AD为∠CAB的平分线，交BC于D，BC=5，BD=2则点D到AB的距离为 ( )课堂延伸2、已知:BD⊥AM于点D,CE⊥AN于E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.课堂延伸