1.2怎样判定三角形全等（SSS）

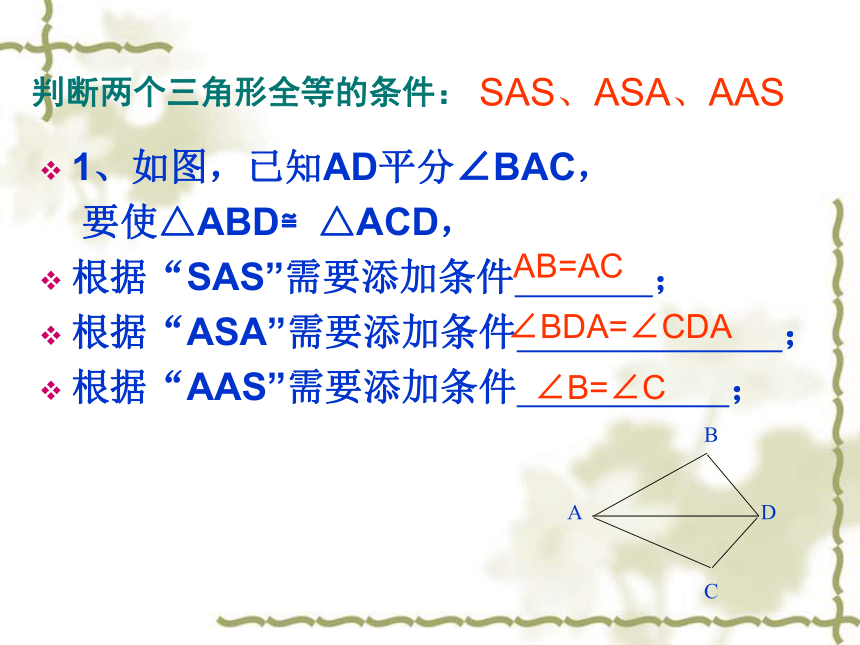
课件14张PPT。全等三角形的判定41、如图，已知AD平分∠BAC，
要使△ABD≌△ACD，
根据“SAS”需要添加条件 ；
根据“ASA”需要添加条件 ；
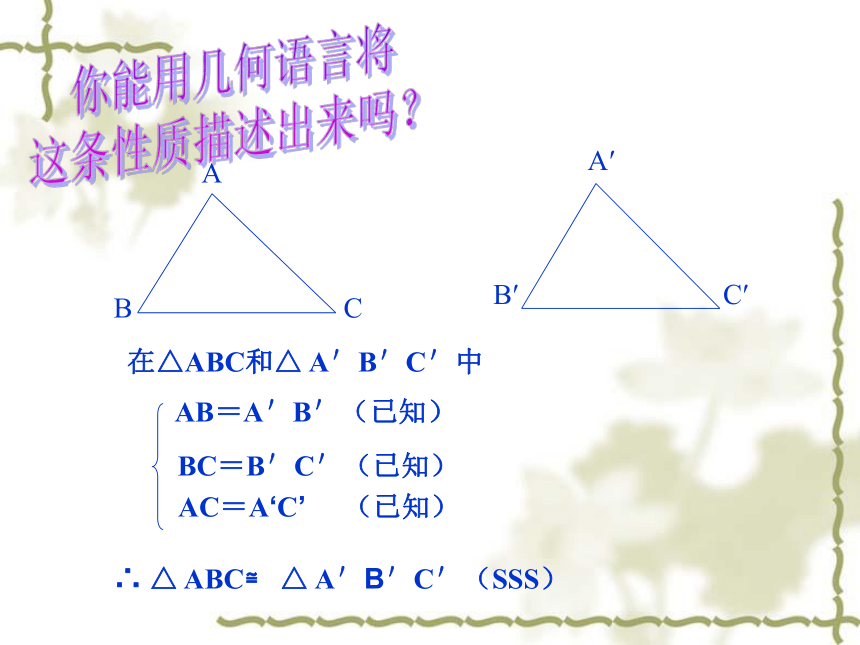
根据“AAS”需要添加条件 ；判断两个三角形全等的条件：AB=AC∠BDA=∠CDA∠B=∠CSAS、ASA、AAS用刻度尺和圆规画一个ΔABC，使AB=4cm，BC=6cm，CA=5cm。画一画三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）判定方法4：AB＝A＇B＇（已知）AC＝A‘C’ （已知）BC＝B＇C＇（已知）∴ △ ABC≌ △ A＇B＇C＇（SSS）在△ABC和△ A＇B＇C＇中你能用几何语言将
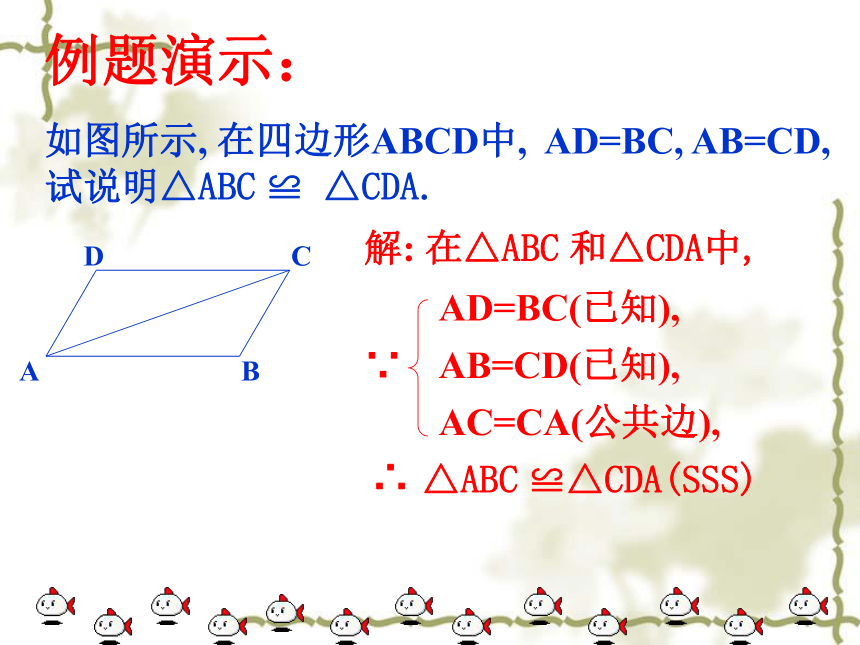
这条性质描述出来吗？例题演示：
如图所示, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
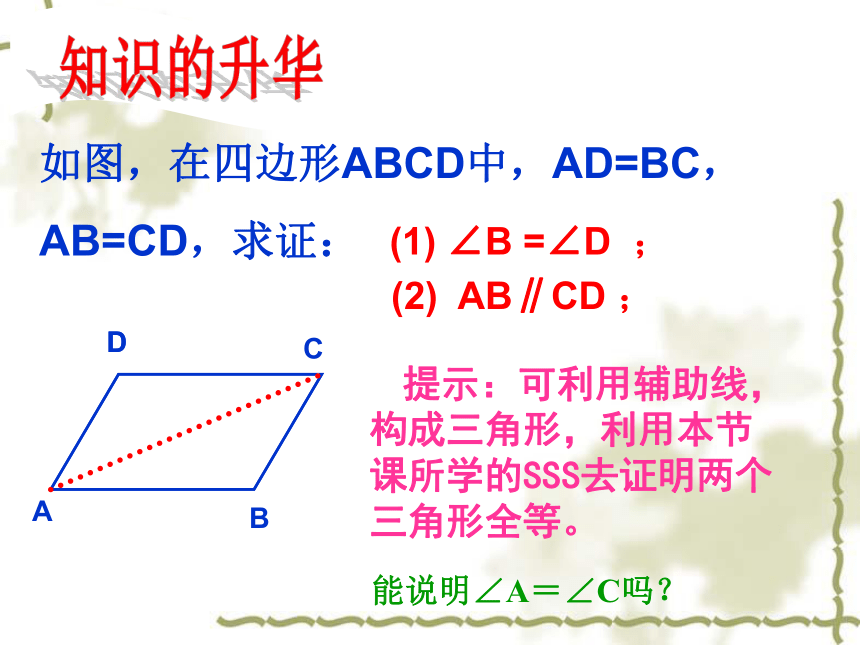
如图，在四边形ABCD中，AD=BC，
AB=CD，求证：DDABC (1) ∠B =∠D ； 提示：可利用辅助线，构成三角形，利用本节课所学的SSS去证明两个三角形全等。(2) AB∥CD ； 能说明∠A＝∠C吗？ 若两个三角形有三个角对应相等，那么这两个三角形是否全等呢？画△ABC , 其中∠A=50°,∠B=60°, ∠C=70°.50°50°60°60°ABCABCA? B? C? 70°70°三个角对应相等的两个三角形不一定全等问题： 一定
(SAS)不一定 一定
(ASA) 一定
(AAS) 一定
(SSS)不一定归纳判定三角形全等至少要有一组边！练一练： 1.如图，AB=DC，AC=DB，△ABC与△DCB全等吗？为什么？△ABO与△DCO全等吗？2. 如图，AB=AD，CB=CD，E是AC上一点，BE与DE相等吗？练一练：巩固练习1.已知AB=AC，BD=CD，则图中对应相等的角有（ ）

A、1对 B、2对 C、3对 D、4对D2. 如图，已知AB=CD，AD=BC，则图中共有全等三角形的对数是（ ） 3. 如图，AD平分∠ BAC，AB=AC，连结BD，CD，并延长交AC，AB于点F、E，则此图形中有（ ）对全等三角形。1. 如图，AC、BD相交于点O，且 AB=DC，AC=BD
求证： （1） ∠A=∠D
（2） OB=OCABCDO提示：做辅助线应用迁移，巩固提高应用迁移，巩固提高 2、如图，△ABC中AB=AC，求证：∠B=∠CD