2022-2023学年人教版九年级数学下册27.2.1相似三角形的判定(2)课件-(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册27.2.1相似三角形的判定(2)课件-(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 08:20:59 | ||
图片预览




文档简介
(共16张PPT)
相似三角形的判定一
(SSS)
课件简介
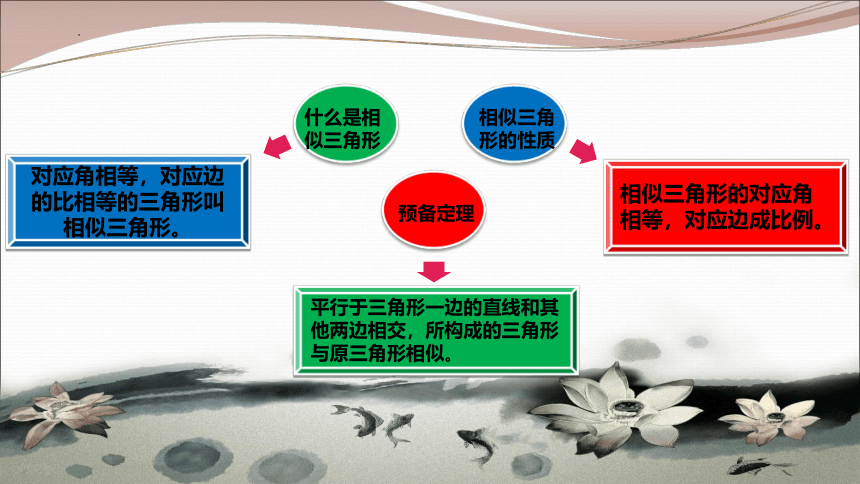
相似三角形的对应角相等,对应边成比例。
对应角相等,对应边的比相等的三角形叫相似三角形。
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
什么是相似三角形
相似三角形的性质
预备定理
相似三角形与全等三角形有什么内在的联系呢?
思 考
?
当两个三角形的相似比为 1 时,它们是全等的,全等是相似的一种特殊情况。
学习三角形全等时我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的方法(SSS,SAS,ASA,AAS)。类似的,判定两个三角形相似时,是不是对所有对应边和对应角都要一一验证呢?
不需要
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
能
思 考
?
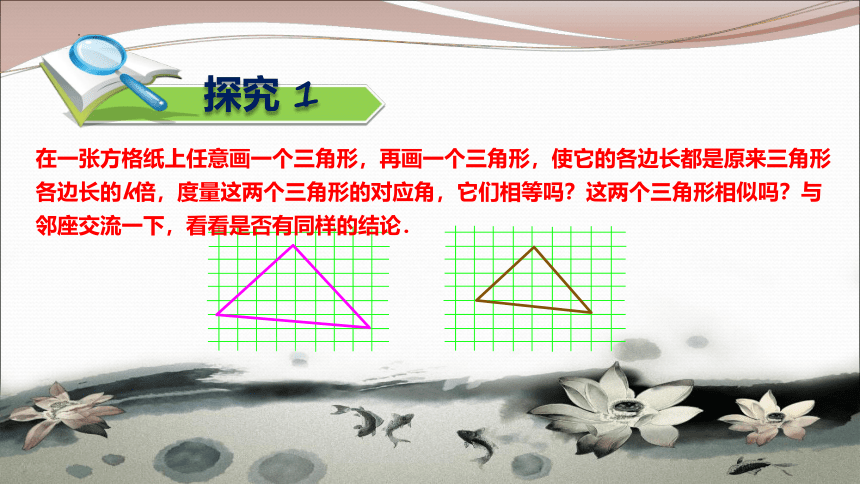
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与邻座交流一下,看看是否有同样的结论.
探究 1
E
D
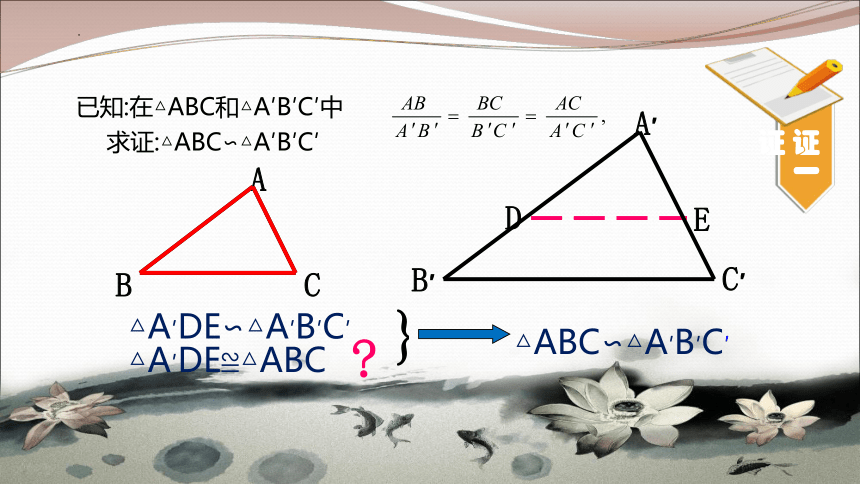
△A′DE≌△ABC
△A′DE∽△A′B′C′
△ABC∽△A′B′C′
已知:在△ABC和△A′B′C′中
求证:△ABC∽△A′B′C′
B′
A′
C′
B
A
C
证一证
几何语言:
结论:三组对应边的比相等的两个三角形相似。
∴△A B C ∽△ABC
∵
根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。
(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
△ABC∽△DEF
不 相 似
△ABC∽△DEF
试一试
例一:如图,判断4×4方格中的两个三角形是否相似, 并说明理由.
E
D
F
B
A
C
例题教学
例二 求证:三角形的三条中位线所组成的三角形 与原三角形相似。
已知:
求证:
如图,DE,DF,EF是△ABC的中位线
△ABC∽△FED
证明:
∵ DE,DF,EF是△ABC的中位线
∴ DE= BC,DF= AC,EF= AB
∴
∴ △ABC∽△DEF
D
A
B
C
E
F
例题教学
一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗?
A
B
C
D
E
N
S
学以致用
选做题:P55 面第4、5题
必做题:P55 面第1、3题
作业
为美化校园,学校决定对东教学楼
后面的一块三角形的空地(如图)进行修整,
现已测量出AB=12m,BC=16m,CA=24m,
请你用适当的比例为这块空地画出图纸。
12m
16m
24m
1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?
两个三角形各边的对应比相等
合作学习
谢谢指导!
相似三角形的判定一
(SSS)
课件简介
相似三角形的对应角相等,对应边成比例。
对应角相等,对应边的比相等的三角形叫相似三角形。
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
什么是相似三角形
相似三角形的性质
预备定理
相似三角形与全等三角形有什么内在的联系呢?
思 考
?
当两个三角形的相似比为 1 时,它们是全等的,全等是相似的一种特殊情况。
学习三角形全等时我们知道,除了可以通过证明对应角相等,对应边相等来判定两个三角形全等外,还有判定的方法(SSS,SAS,ASA,AAS)。类似的,判定两个三角形相似时,是不是对所有对应边和对应角都要一一验证呢?
不需要
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
能
思 考
?
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与邻座交流一下,看看是否有同样的结论.
探究 1
E
D
△A′DE≌△ABC
△A′DE∽△A′B′C′
△ABC∽△A′B′C′
已知:在△ABC和△A′B′C′中
求证:△ABC∽△A′B′C′
B′
A′
C′
B
A
C
证一证
几何语言:
结论:三组对应边的比相等的两个三角形相似。
∴△A B C ∽△ABC
∵
根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。
(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
△ABC∽△DEF
不 相 似
△ABC∽△DEF
试一试
例一:如图,判断4×4方格中的两个三角形是否相似, 并说明理由.
E
D
F
B
A
C
例题教学
例二 求证:三角形的三条中位线所组成的三角形 与原三角形相似。
已知:
求证:
如图,DE,DF,EF是△ABC的中位线
△ABC∽△FED
证明:
∵ DE,DF,EF是△ABC的中位线
∴ DE= BC,DF= AC,EF= AB
∴
∴ △ABC∽△DEF
D
A
B
C
E
F
例题教学
一条河流,在河流的北岸点A处有一根高压电线杆。河流的南岸点B处有一颗大树。且电线杆在大树的正北方向上。在大树的正东方的点C处有一雕像,你能利用本节课学习的知识大致测算出电线杆A与大树B之间的距离吗?
A
B
C
D
E
N
S
学以致用
选做题:P55 面第4、5题
必做题:P55 面第1、3题
作业
为美化校园,学校决定对东教学楼
后面的一块三角形的空地(如图)进行修整,
现已测量出AB=12m,BC=16m,CA=24m,
请你用适当的比例为这块空地画出图纸。
12m
16m
24m
1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?
两个三角形各边的对应比相等
合作学习
谢谢指导!
