2022—2023学年人教版数学九年级上册22.3实际问题与二次函数(拱桥问题)课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册22.3实际问题与二次函数(拱桥问题)课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 09:48:57 | ||
图片预览



文档简介
(共17张PPT)
拱桥问题
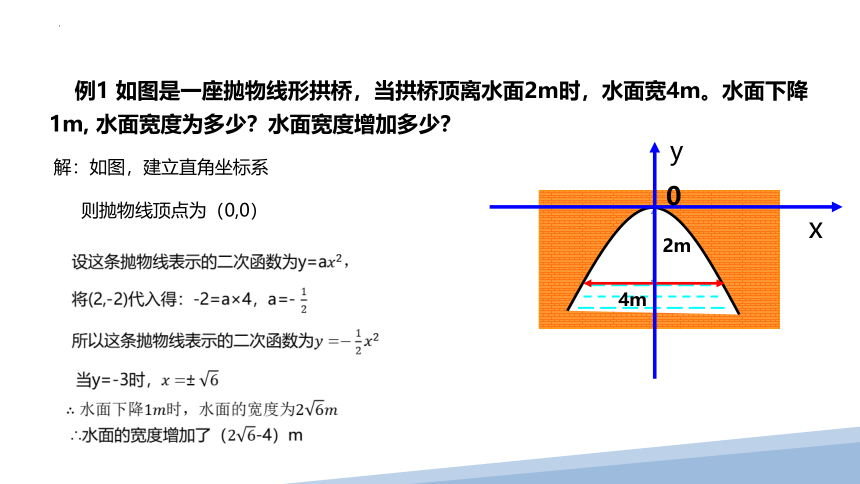
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
解:如图,建立直角坐标系
则抛物线顶点为(0,0)
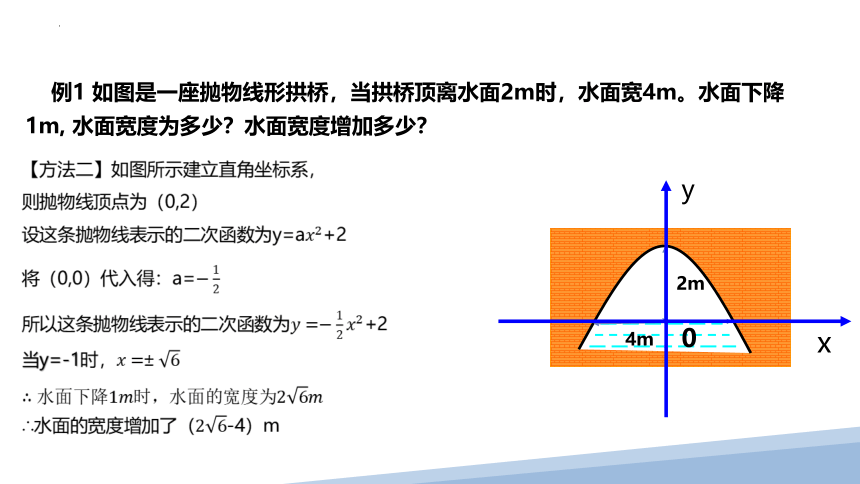
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
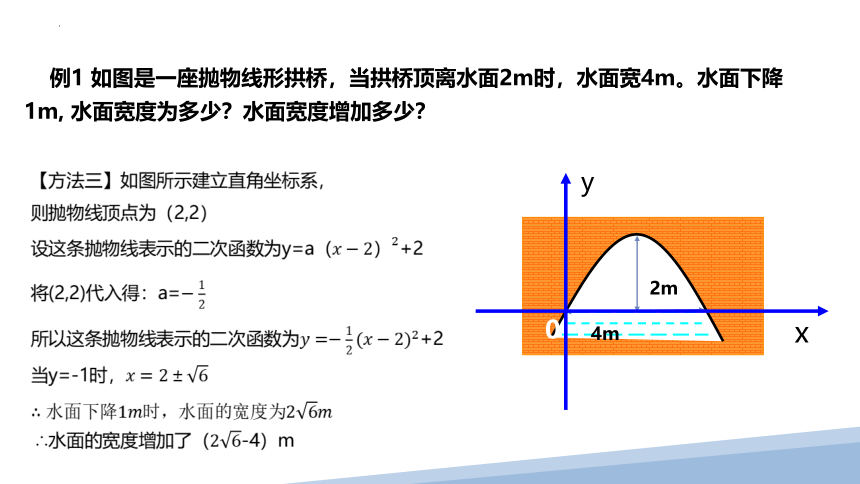
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
利用函解决拱桥问题
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
【方法四】根据坐标系位置,尝试求解
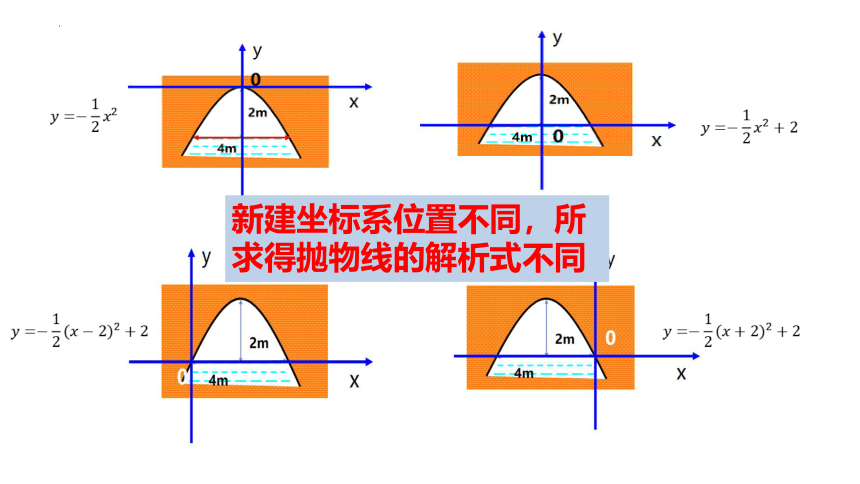
新建坐标系位置不同,所求得抛物线的解析式不同
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
练习1如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面上升1m,水面宽度减少_____m.
练习2 如图是抛物线型拱桥,当拱顶离水面 2m 时,水面宽4m,当水面宽度为 m时,水面下降了____m.
x
y
x
y
0
x
y
0
x
y
0
x
y
0
x
y
0
设OE=n
则B(3,-n)
D(4,-n-3)
设y=a
将B、D代入得:
∴y=
当x=4时,y=
∴OF==6.85…≈6.9
设y=
将B(3,0) D(4, -3)代入得:
解得
∴y=
设y=
将B(3,3) D(4, 0)代入得:
解得
∴y=
∴大门高为≈6.9米
∴大门高为≈6.9米
当x=0时,y=
例2 抛物线形拱门的示意图如图所示,底部宽AB为6米,最高点O距地面5米.现有一辆集装箱车,宽为2.8米,高为4米,请通过计算说明此车能否通过拱门.
x
y
教学案册 18页课堂练习第1题
A
C
B
x
y
0
解:(1)如图,建立直角坐标系
由题可知抛物线顶点为(0,3.6),B(,0)
∴设抛物线解析式为y=3.6
将B(,0)代入得
0=3.6
解得=0.9
∴y=3.6
(2)当x=时, y=
2.7
∴这辆汽车不能顺利通过大门
当x=1时,y=1+4=
∴所以能通过
分层作业册41页 7题
(1)直接写出c= ;
(2)求该隧道截面的最大跨度(即AB的长度)是多少米?
(3)该隧道为双向车道,现有一辆运货卡车高4米、宽3米,问这辆卡车能否顺利通过隧道?(不考虑双向车道中间防护栏宽度)请说明理由.
分层作业册42页 12题
x
y
0
解:(1)如图,建立直角坐标系
由题可知抛物线顶点为(0,12),B(,0)
∴设抛物线解析式为y=
将B(,0)代入得
0=
解得=
∴y=
(2)当x=时
y=
126=6米
6÷0.25=24小时
答:水过警戒线后24小时淹到拱桥顶.
拱桥问题
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
解:如图,建立直角坐标系
则抛物线顶点为(0,0)
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
利用函解决拱桥问题
例1 如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。水面下降1m, 水面宽度为多少?水面宽度增加多少?
2m
4m
x
0
y
【方法四】根据坐标系位置,尝试求解
新建坐标系位置不同,所求得抛物线的解析式不同
解决拱桥问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
练习1如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面上升1m,水面宽度减少_____m.
练习2 如图是抛物线型拱桥,当拱顶离水面 2m 时,水面宽4m,当水面宽度为 m时,水面下降了____m.
x
y
x
y
0
x
y
0
x
y
0
x
y
0
x
y
0
设OE=n
则B(3,-n)
D(4,-n-3)
设y=a
将B、D代入得:
∴y=
当x=4时,y=
∴OF==6.85…≈6.9
设y=
将B(3,0) D(4, -3)代入得:
解得
∴y=
设y=
将B(3,3) D(4, 0)代入得:
解得
∴y=
∴大门高为≈6.9米
∴大门高为≈6.9米
当x=0时,y=
例2 抛物线形拱门的示意图如图所示,底部宽AB为6米,最高点O距地面5米.现有一辆集装箱车,宽为2.8米,高为4米,请通过计算说明此车能否通过拱门.
x
y
教学案册 18页课堂练习第1题
A
C
B
x
y
0
解:(1)如图,建立直角坐标系
由题可知抛物线顶点为(0,3.6),B(,0)
∴设抛物线解析式为y=3.6
将B(,0)代入得
0=3.6
解得=0.9
∴y=3.6
(2)当x=时, y=
2.7
∴这辆汽车不能顺利通过大门
当x=1时,y=1+4=
∴所以能通过
分层作业册41页 7题
(1)直接写出c= ;
(2)求该隧道截面的最大跨度(即AB的长度)是多少米?
(3)该隧道为双向车道,现有一辆运货卡车高4米、宽3米,问这辆卡车能否顺利通过隧道?(不考虑双向车道中间防护栏宽度)请说明理由.
分层作业册42页 12题
x
y
0
解:(1)如图,建立直角坐标系
由题可知抛物线顶点为(0,12),B(,0)
∴设抛物线解析式为y=
将B(,0)代入得
0=
解得=
∴y=
(2)当x=时
y=
126=6米
6÷0.25=24小时
答:水过警戒线后24小时淹到拱桥顶.
同课章节目录
