加减消元法[下学期]
图片预览





文档简介
课件29张PPT。主要步骤: 基本思路:写解求解代入一元消去一个元分别求出两个未知数的值写出方程组的解变形用一个未知数的代数式
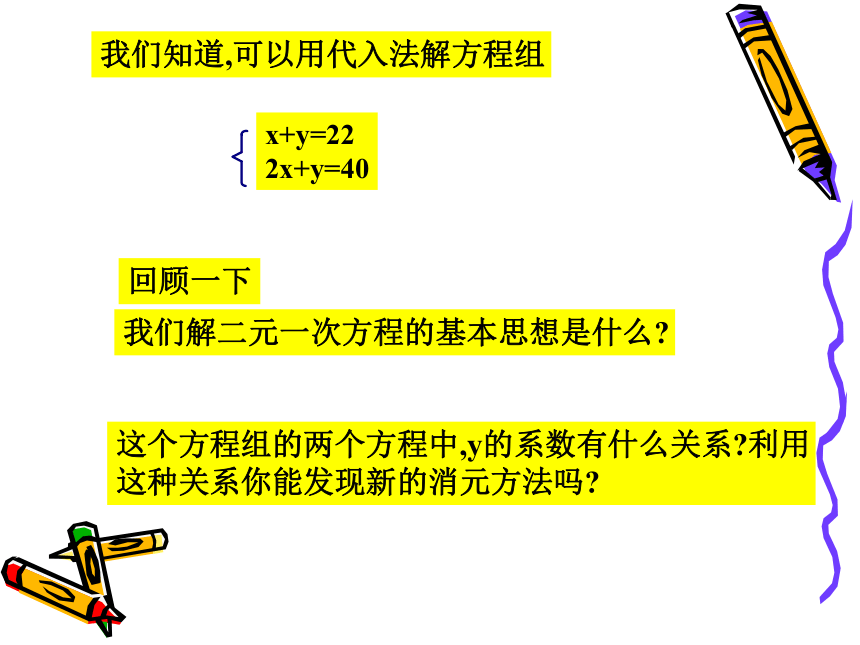
表示另一个未知数消元: 二元1、解二元一次方程组的基本思路是什么?2、用代入法解方程的步骤是什么?复习:一元我们知道,可以用代入法解方程组x+y=22
2x+y=40回顾一下我们解二元一次方程的基本思想是什么?这个方程组的两个方程中,y的系数有什么关系?利用
这种关系你能发现新的消元方法吗?x+y=22
2x+y=40这两个方程中未知数y的系数相同,①
②②-①可消去未知数y,得
x=18
把x=18代入①,得
y=4.①-②也能消去
未知数y,求得
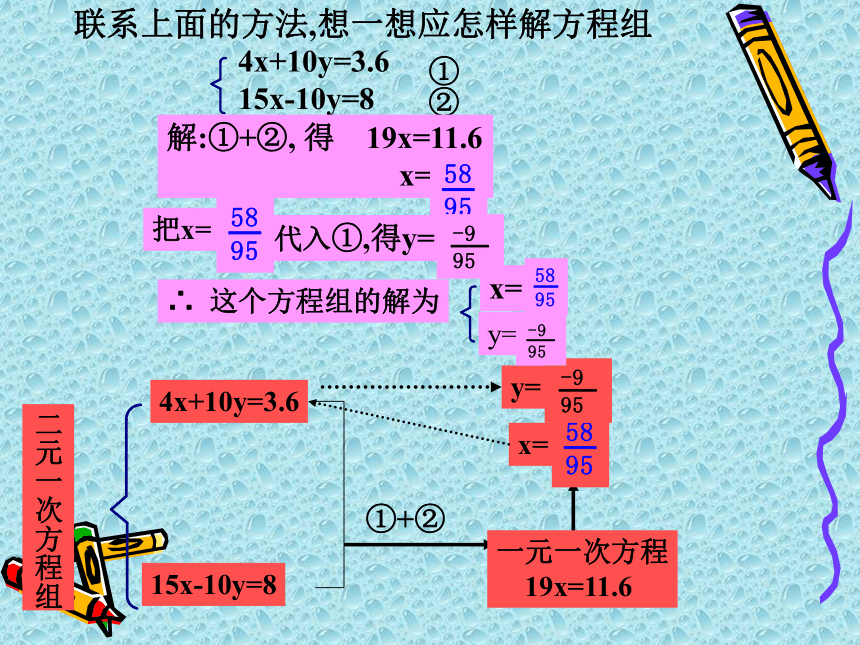
x吗? 联系上面的方法,想一想应怎样解方程组4x+10y=3.6
15x-10y=8①②解:①+②, 得 19x=11.6
x=二元一次方程组4x+10y=3.615x-10y=8一元一次方程
19x=11.6x=y=把x=代入①,得y=∴ 这个方程组的解为x=y=①+②
加减消元解二元一次方程组想一想: 方程具有什么特点时,用加减法消元?归纳:
我们发现,如果二元一次方程组的两个方程中
某个未知数的系数相同或互为相反数,就可以直接用
加减法显得非常简便.来做一做下面的例题吧.例1.用加减法解下列方程组:(1)4x+y=2
4x-3y=-6(2)3x+2y=-1
2x+4y=-7①②①②解: (1)①-②, 得
4y=8
y=2
把y=2代入方程①,得
x=0(2) ①×2-②, 得
4x=5
x=1.25
把x=1.25代入②,得
y=-2.375 两个二元一次方程中同一未知数相反或相等时,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.归纳:通过上一个例子我们知道,当两个方程中某个未知数的系数
成倍数关系时,我们也可以用加减法,只不过在加或减之前,
可以先将一个方程变形成与另一个方程中相同未知数的系
数相同,这样就可以达到消元的目的.看一看下面这个例子,我们又该如何解决呢?3x+4y=16
5x-6y=33能用加减法做吗?怎么做呢?试试看!解:①×3,得 9x+12y=48 ③
②×2,得 10x-12y=66 ④
③+④,得 19x=114
x=6
把x=6代入① ,得
3×6+4y=16
4y=﹣2
y=﹣所以这个方程组的解是X=6y=﹣用加减法消去x应如何解?1.用加减法解下面方程组时,你认为先消去哪个未知数
比较简单,填写消元的方法:(1)3x-2y=15
5x-4y=23消元方法:__________①②(2)7m-3n=1
2n+3m=-2①②消元方法:_______________.2.书本P111练习第一题.①×2-②①×2+②×3小结 本节课,我们学习了二元一次方程组的另一种
解法------加减法,即通过把方程组中的两个方程进
行加或减,消去一个未知数,化“二元”为“一元”.
用加减法解比较简便的二元一次方程组主要
分为以下三种:
(1)两个方程中某个未知数的系数相同或互为相反数,
这时直接将两个方程加或减即可消元;
(2)两个方程中某个未知数的系数存在倍数关系,这时
须将其中一个方程两边乘这个倍数,然后在加或减即
可消元;
(3)两个方程中的未知数的系数不存在任何关系,这时
须找到一个未知数,将两个方程两边都乘某个数,从而
将这两个方程中这个未知数的系数变的相同,再加减.1.把下列方程改写成用含x的代数式表示y的形式:
(1)2x+y=6; (2)2x-3y-10=0.
2.再将上面方程改写成用含y的代数式表示x的形式.3.用代入消元法解方程组x-2y=3 ①
2x+y=1②解:由②,得y=________③, ③代入①,得x-2( )=3
解得x=________,再把x的值代入③,得y=_______,
所以,原方程组的解是x=___
y=___.4.用代入法解下列方程组.(1)15%x+25%y=50×65%
x+y=150(2)5.如果二元一次方程组ax-by=1,
3ax+2by=23的解是x=5
y=4.求a-b的值.练习一五、作业1、课本P-112[习题8.2] 3
2、思考题:
在解二元一次方程组中, 代入法
和加减法有什么异同点?谢谢光临指导问题 怎样解下面的二元一次方程组呢?小明思路把②变形得可以直接代入①呀!小彬思路按照小丽的思路,你能消去
一个未知数吗?小丽(3x + 5y)+(2x - 5y)=21 + (-11)
分析: 3X+5y +2x - 5y=10 ①左边 + ② 左边 = ① 左边 + ②左边5x+0y =10
5x=10
所以原方程组的解是 解:由①+②得: 5x=10 把x=2代入①,得 x=2y=3 参考小丽的思路,怎样解下面的二元一次方程组呢?观察方程组中的两个方程,未知数x的系数
相等,都是2.把这两个方程两边分别相减,
就可以消去未知数x,同样得到一个一元一
次方程.①②分析:所以原方程组的解是解:把 ②-①得:8y=-8
y=-1把y =-1代入①,得
2x-5╳(-1)=7解得:x=1分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x一.填空题:只要两边只要两边练习二.选择题B2.方程组3x+2y=133x-2y=5消去y后所得的方程是( )BA.6x=8B.6x=18C.6x=5D.x=18三、指出下列方程组求解过程中有错误步骤,并给予订正:7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①①②②3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6解: ①-②,得
2x=4+4,
x=4解: ①+②,得
8x=16
x =2
看看你掌握了吗?四. 用加减法解方程组则a+b=5上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?4.议一议:主要步骤:
特点:基本思路:写解求解加减二元一元加减消元:消去一个元分别求出两个未知数的值写出原方程组的解同一个未知数的系数相同或互为相反数主要步骤:
基本思路:写解求解加减二元一元加减消元:消去一个元求出两个未知数的值写出方程组的解小结 :1.加减消元法解方程组基本思路是什么?
主要步骤有哪些?变形同一个未知数的系
数相同或互为相反数2. 二元一次方程组解法有 .代入法、加减法
表示另一个未知数消元: 二元1、解二元一次方程组的基本思路是什么?2、用代入法解方程的步骤是什么?复习:一元我们知道,可以用代入法解方程组x+y=22
2x+y=40回顾一下我们解二元一次方程的基本思想是什么?这个方程组的两个方程中,y的系数有什么关系?利用
这种关系你能发现新的消元方法吗?x+y=22
2x+y=40这两个方程中未知数y的系数相同,①
②②-①可消去未知数y,得
x=18
把x=18代入①,得
y=4.①-②也能消去
未知数y,求得
x吗? 联系上面的方法,想一想应怎样解方程组4x+10y=3.6
15x-10y=8①②解:①+②, 得 19x=11.6
x=二元一次方程组4x+10y=3.615x-10y=8一元一次方程
19x=11.6x=y=把x=代入①,得y=∴ 这个方程组的解为x=y=①+②
加减消元解二元一次方程组想一想: 方程具有什么特点时,用加减法消元?归纳:
我们发现,如果二元一次方程组的两个方程中
某个未知数的系数相同或互为相反数,就可以直接用
加减法显得非常简便.来做一做下面的例题吧.例1.用加减法解下列方程组:(1)4x+y=2
4x-3y=-6(2)3x+2y=-1
2x+4y=-7①②①②解: (1)①-②, 得
4y=8
y=2
把y=2代入方程①,得
x=0(2) ①×2-②, 得
4x=5
x=1.25
把x=1.25代入②,得
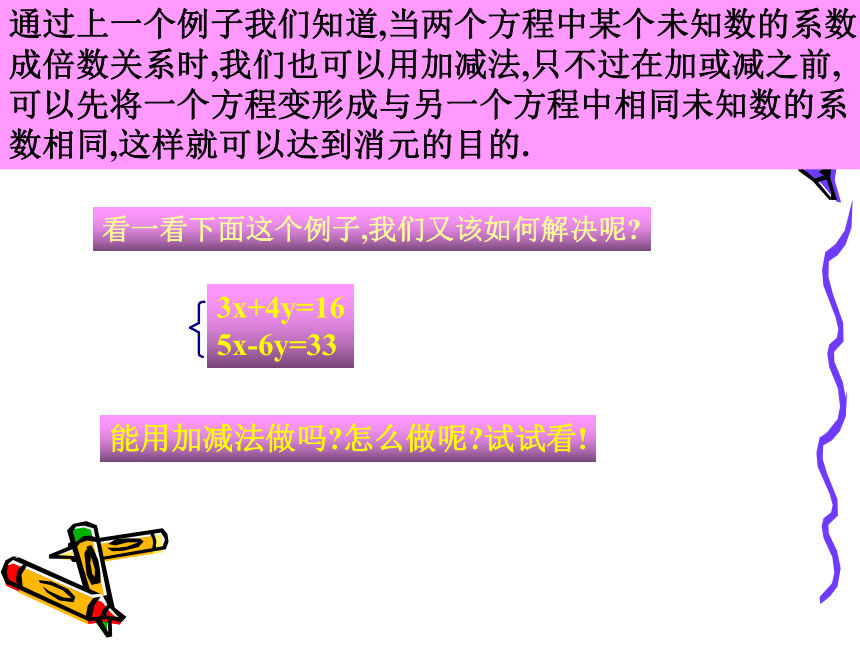
y=-2.375 两个二元一次方程中同一未知数相反或相等时,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.归纳:通过上一个例子我们知道,当两个方程中某个未知数的系数
成倍数关系时,我们也可以用加减法,只不过在加或减之前,
可以先将一个方程变形成与另一个方程中相同未知数的系
数相同,这样就可以达到消元的目的.看一看下面这个例子,我们又该如何解决呢?3x+4y=16
5x-6y=33能用加减法做吗?怎么做呢?试试看!解:①×3,得 9x+12y=48 ③
②×2,得 10x-12y=66 ④
③+④,得 19x=114
x=6
把x=6代入① ,得
3×6+4y=16
4y=﹣2
y=﹣所以这个方程组的解是X=6y=﹣用加减法消去x应如何解?1.用加减法解下面方程组时,你认为先消去哪个未知数
比较简单,填写消元的方法:(1)3x-2y=15
5x-4y=23消元方法:__________①②(2)7m-3n=1
2n+3m=-2①②消元方法:_______________.2.书本P111练习第一题.①×2-②①×2+②×3小结 本节课,我们学习了二元一次方程组的另一种
解法------加减法,即通过把方程组中的两个方程进
行加或减,消去一个未知数,化“二元”为“一元”.
用加减法解比较简便的二元一次方程组主要
分为以下三种:
(1)两个方程中某个未知数的系数相同或互为相反数,
这时直接将两个方程加或减即可消元;
(2)两个方程中某个未知数的系数存在倍数关系,这时
须将其中一个方程两边乘这个倍数,然后在加或减即
可消元;
(3)两个方程中的未知数的系数不存在任何关系,这时
须找到一个未知数,将两个方程两边都乘某个数,从而
将这两个方程中这个未知数的系数变的相同,再加减.1.把下列方程改写成用含x的代数式表示y的形式:
(1)2x+y=6; (2)2x-3y-10=0.
2.再将上面方程改写成用含y的代数式表示x的形式.3.用代入消元法解方程组x-2y=3 ①
2x+y=1②解:由②,得y=________③, ③代入①,得x-2( )=3
解得x=________,再把x的值代入③,得y=_______,
所以,原方程组的解是x=___
y=___.4.用代入法解下列方程组.(1)15%x+25%y=50×65%
x+y=150(2)5.如果二元一次方程组ax-by=1,
3ax+2by=23的解是x=5
y=4.求a-b的值.练习一五、作业1、课本P-112[习题8.2] 3
2、思考题:
在解二元一次方程组中, 代入法
和加减法有什么异同点?谢谢光临指导问题 怎样解下面的二元一次方程组呢?小明思路把②变形得可以直接代入①呀!小彬思路按照小丽的思路,你能消去
一个未知数吗?小丽(3x + 5y)+(2x - 5y)=21 + (-11)
分析: 3X+5y +2x - 5y=10 ①左边 + ② 左边 = ① 左边 + ②左边5x+0y =10
5x=10
所以原方程组的解是 解:由①+②得: 5x=10 把x=2代入①,得 x=2y=3 参考小丽的思路,怎样解下面的二元一次方程组呢?观察方程组中的两个方程,未知数x的系数
相等,都是2.把这两个方程两边分别相减,
就可以消去未知数x,同样得到一个一元一
次方程.①②分析:所以原方程组的解是解:把 ②-①得:8y=-8
y=-1把y =-1代入①,得
2x-5╳(-1)=7解得:x=1分别相加y1.已知方程组x+3y=172x-3y=6两个方程就可以消去未知数分别相减2.已知方程组25x-7y=1625x+6y=10两个方程就可以消去未知数x一.填空题:只要两边只要两边练习二.选择题B2.方程组3x+2y=133x-2y=5消去y后所得的方程是( )BA.6x=8B.6x=18C.6x=5D.x=18三、指出下列方程组求解过程中有错误步骤,并给予订正:7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①①②②3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6解: ①-②,得
2x=4+4,
x=4解: ①+②,得
8x=16
x =2
看看你掌握了吗?四. 用加减法解方程组则a+b=5上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?4.议一议:主要步骤:
特点:基本思路:写解求解加减二元一元加减消元:消去一个元分别求出两个未知数的值写出原方程组的解同一个未知数的系数相同或互为相反数主要步骤:
基本思路:写解求解加减二元一元加减消元:消去一个元求出两个未知数的值写出方程组的解小结 :1.加减消元法解方程组基本思路是什么?
主要步骤有哪些?变形同一个未知数的系
数相同或互为相反数2. 二元一次方程组解法有 .代入法、加减法
