冀教版数学九年级下册 30.4二次函数的应用同步练习(含答案)
文档属性
| 名称 | 冀教版数学九年级下册 30.4二次函数的应用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 281.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 10:35:44 | ||
图片预览




文档简介
30.4二次函数的应用同步练习冀教版数学九年级下册
一、单选题(共30分)
1.(本题3分)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
2.(本题3分)某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.(本题3分)在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
4.(本题3分)如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m.那么水位下降1m时,水面的宽度为( )
A. B. C. D.
5.(本题3分)某超市将进价为40元件的商品按50元/件出售时,每月可售出500件.经试销发现,该商品售价每上涨1元,其月销量就减少10件.超市为了每月获利8000元,则每件应涨价多少元?若设每件应涨价x元,则依据题意可列方程为( )
A. B.
C. D.
6.(本题3分)如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
7.(本题3分)在羽毛球比赛中,某次羽毛球的运动路线呈抛物线形,羽毛球距地面的高度与水平距离之间的关系如图所示,点B为落地点,且,,羽毛球到达的最高点到y轴的距离为,那么羽毛球到达最高点时离地面的高度为( )
A. B. C. D.
8.(本题3分)已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
9.(本题3分)记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
10.(本题3分)某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
二、填空题(共30分)
11.(本题3分)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
12.(本题3分)如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.则S与x的函数关系式是____________,自变量x的取值范围是____________.
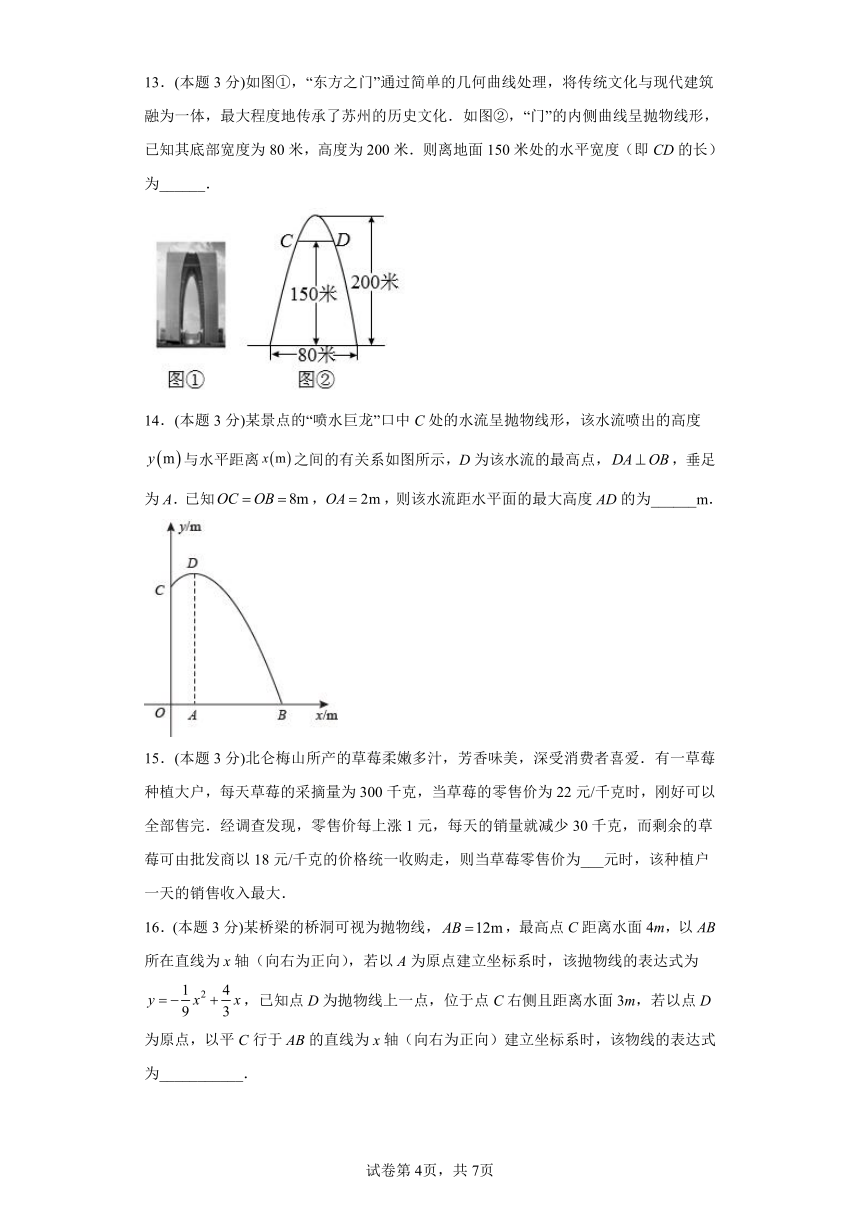
13.(本题3分)如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
14.(本题3分)某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度与水平距离之间的有关系如图所示,D为该水流的最高点,,垂足为A.已知,,则该水流距水平面的最大高度AD的为______m.
15.(本题3分)北仑梅山所产的草莓柔嫩多汁,芳香味美,深受消费者喜爱.有一草莓种植大户,每天草莓的采摘量为300千克,当草莓的零售价为22元/千克时,刚好可以全部售完.经调查发现,零售价每上涨1元,每天的销量就减少30千克,而剩余的草莓可由批发商以18元/千克的价格统一收购走,则当草莓零售价为___元时,该种植户一天的销售收入最大.
16.(本题3分)某桥梁的桥洞可视为抛物线,,最高点C距离水面4m,以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为,已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平C行于AB的直线为x轴(向右为正向)建立坐标系时,该物线的表达式为___________.
17.(本题3分)某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
18.(本题3分)已知在平面直角坐标系中,点的坐标为是抛物线对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使为直角三角形的点的个数也随之确定.若抛物线的对称轴上存在3个不同的点,使为直角三角形,则的值是____.
19.(本题3分)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
20.(本题3分)从地面竖直向上抛射一个小球,小球的高度h (米)与运动时间t(秒)之间的关系式为h=30t﹣5t2,那么小球抛出___秒后落地.
三、解答题(共60分)
21.(本题12分)某文具店购进一批单价为12元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价的1.5倍,通过分析销售情况,发现每天的销售量y(件)与销售单价x(元)满足一次函数关系,且当时,;当时,.
(1)求y与x之间的函数关系式;
(2)这种学习用品的销售单价定为多少时,每天可获得最大利润,最大利润是多少元?
22.(本题12分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大?最大值为多少?
23.(本题12分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
24.(本题12分)某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
(1)求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)
(2)若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
(3)超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
25.(本题12分)如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.C
4.B
5.C
6.A
7.D
8.D
9.D
10.B
11.##
12. S=-3x2+24x ≤x<8
13.40米
14.9
15.25
16.##
17.11
18.2或
19.2
20.6
21.(1)y与x之间的函数关系式为
(2)这种学习用品的销售单价定为16元时,每天可获得最大利润,最大利润是160元.
22.(1)x的值为2m;
(2)当时,矩形养殖场的总面积最大,最大值为 m2
23.(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
24.(1);(2)70元;(3)80元.
25.(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(,)或(,).
答案第1页,共2页
答案第1页,共2页
一、单选题(共30分)
1.(本题3分)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
2.(本题3分)某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.(本题3分)在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
4.(本题3分)如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m.那么水位下降1m时,水面的宽度为( )
A. B. C. D.
5.(本题3分)某超市将进价为40元件的商品按50元/件出售时,每月可售出500件.经试销发现,该商品售价每上涨1元,其月销量就减少10件.超市为了每月获利8000元,则每件应涨价多少元?若设每件应涨价x元,则依据题意可列方程为( )
A. B.
C. D.
6.(本题3分)如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
7.(本题3分)在羽毛球比赛中,某次羽毛球的运动路线呈抛物线形,羽毛球距地面的高度与水平距离之间的关系如图所示,点B为落地点,且,,羽毛球到达的最高点到y轴的距离为,那么羽毛球到达最高点时离地面的高度为( )
A. B. C. D.
8.(本题3分)已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
9.(本题3分)记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825 B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900 D.y=﹣2(x﹣65)2+2000
10.(本题3分)某超市销售一种商品,每件成本为元,销售人员经调查发现,该商品每月的销售量(件)与销售单价(元)之间满足函数关系式,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.元,元 B.元,元
C.元,元 D.元,元
二、填空题(共30分)
11.(本题3分)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
12.(本题3分)如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.则S与x的函数关系式是____________,自变量x的取值范围是____________.
13.(本题3分)如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为______.
14.(本题3分)某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度与水平距离之间的有关系如图所示,D为该水流的最高点,,垂足为A.已知,,则该水流距水平面的最大高度AD的为______m.
15.(本题3分)北仑梅山所产的草莓柔嫩多汁,芳香味美,深受消费者喜爱.有一草莓种植大户,每天草莓的采摘量为300千克,当草莓的零售价为22元/千克时,刚好可以全部售完.经调查发现,零售价每上涨1元,每天的销量就减少30千克,而剩余的草莓可由批发商以18元/千克的价格统一收购走,则当草莓零售价为___元时,该种植户一天的销售收入最大.
16.(本题3分)某桥梁的桥洞可视为抛物线,,最高点C距离水面4m,以AB所在直线为x轴(向右为正向),若以A为原点建立坐标系时,该抛物线的表达式为,已知点D为抛物线上一点,位于点C右侧且距离水面3m,若以点D为原点,以平C行于AB的直线为x轴(向右为正向)建立坐标系时,该物线的表达式为___________.
17.(本题3分)某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
18.(本题3分)已知在平面直角坐标系中,点的坐标为是抛物线对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使为直角三角形的点的个数也随之确定.若抛物线的对称轴上存在3个不同的点,使为直角三角形,则的值是____.
19.(本题3分)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
20.(本题3分)从地面竖直向上抛射一个小球,小球的高度h (米)与运动时间t(秒)之间的关系式为h=30t﹣5t2,那么小球抛出___秒后落地.
三、解答题(共60分)
21.(本题12分)某文具店购进一批单价为12元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价的1.5倍,通过分析销售情况,发现每天的销售量y(件)与销售单价x(元)满足一次函数关系,且当时,;当时,.
(1)求y与x之间的函数关系式;
(2)这种学习用品的销售单价定为多少时,每天可获得最大利润,最大利润是多少元?
22.(本题12分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大?最大值为多少?
23.(本题12分)一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
24.(本题12分)某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
(1)求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)
(2)若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
(3)超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
25.(本题12分)如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.C
4.B
5.C
6.A
7.D
8.D
9.D
10.B
11.##
12. S=-3x2+24x ≤x<8
13.40米
14.9
15.25
16.##
17.11
18.2或
19.2
20.6
21.(1)y与x之间的函数关系式为
(2)这种学习用品的销售单价定为16元时,每天可获得最大利润,最大利润是160元.
22.(1)x的值为2m;
(2)当时,矩形养殖场的总面积最大,最大值为 m2
23.(1)y=-x2+4;(2)能安全通过,见解析;(3)n=4时,L有最大值,最大值为14
24.(1);(2)70元;(3)80元.
25.(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(,)或(,).
答案第1页,共2页
答案第1页,共2页
