8.2消元(一)[下学期]
文档属性
| 名称 | 8.2消元(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-15 00:00:00 | ||
图片预览




文档简介
课件11张PPT。8.2消元(一)上面的二元一次方程组和一元一次方程有什么关系?观察思考:
1.在一元一次方程解法中,列方程时所用的等量关系是什么?
2.方程②所表示的等量关系是什么?
3.方程②与③的等量关系相同,那么它们的区别在哪里?
4.怎样使方程②中含有的两个未知数变为只含有一个未知数呢? 两个方程中同一个字母代表的含义相同,只要将方程①
变形为y=22-x代入方程②.由此一来,二元化为一元了.
解得x=18. 把X=18代入y=22-x,得y=4,从而得到二元一次
方程组的解是 上面解方程组的基本思路是什么?主要步骤有哪些?基本思路:“消元”——把“二元”变为“一元”. 主要步骤:
将一个方程中的某个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,化二元一次方程组为一元一次方程.进而求得这个二元一次方程组的解.
这种方法叫做代入消元法,简称代入法.
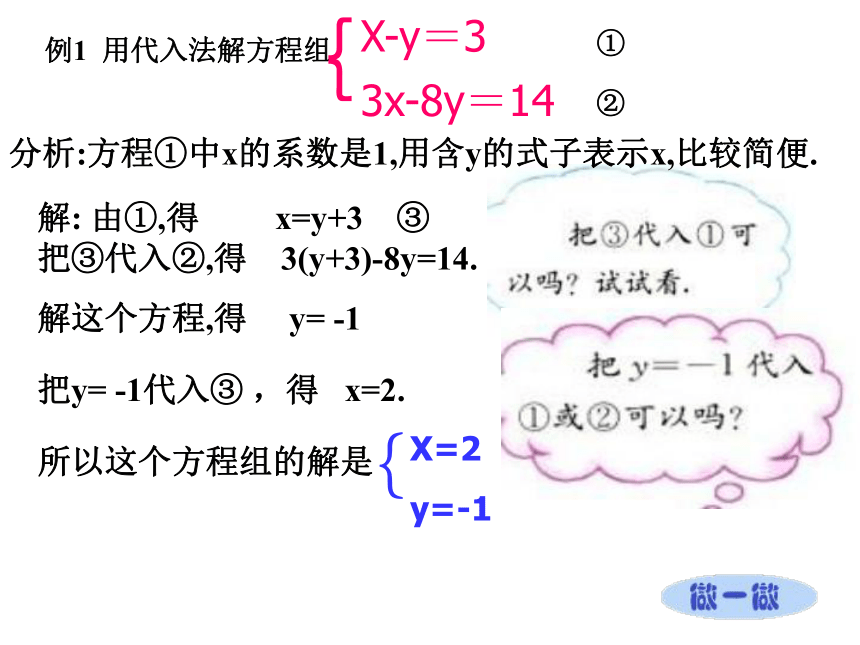
例1 用代入法解方程组①
②解: 由①,得 x=y+3 ③
把③代入②,得 3(y+3)-8y=14.解这个方程,得 y= -1把y= -1代入③ ,得 x=2.所以这个方程组的解是分析:方程①中x的系数是1,用含y的式子表示x,比较简便.例2根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),
两种产品的销售数量比(按瓶计算)为2:5.某厂每天生产这种
消毒液22.5吨,这些消毒液应该分装大.小瓶装两种产品各
多少瓶?解:设这些消毒液应分装x大瓶和y小瓶.
由题意,得
①
②解这个方程,得 x= 20000.
把x= 20000代入③ ,得 y=50000.
所以这个方程组的解是
答:这个工厂一天应生产20000大瓶和50000小瓶消毒液.大瓶所装消毒液+小瓶所装消毒液=总生产量解(1) y=2x-3
(2) y=1-3x①
②解:把①代入②,得
3x+2(2x-3)=8.
3x+4x-6=8
7x=14
x=2
把x= 2代入① ,得 y=1.
所以这个方程组的解是
①
②解: 由①,得 y=2x-5 ③
把③代入②,得
3x+4(2x-5)=2.
解这个方程,得 x=2
把x= 2代入③ ,得 y=-1.
所以这个方程组的解是解:设有x支篮球队和y支排球队参赛.
由题意,得
①
②由①, 得 y =48- x ③
把③代入②,得 10x+12(48-x)=520
解这个方程,得 x= 28.
把x= 28代入③ ,得 y=20.
所以这个方程组的解是
P107解:设骑车用x小时,步行用y小时.
由题意,得
①
②由①, 得 y =1- x ③
把③代入②,得 25x+5(1-x)=20所以这个方程组的解是
本节课你有什么收获?1.解方程组的基本思路:“消元”——把“二元”变为“一元”.2.解方程组的方法:代入消元法.
1.在一元一次方程解法中,列方程时所用的等量关系是什么?
2.方程②所表示的等量关系是什么?
3.方程②与③的等量关系相同,那么它们的区别在哪里?
4.怎样使方程②中含有的两个未知数变为只含有一个未知数呢? 两个方程中同一个字母代表的含义相同,只要将方程①
变形为y=22-x代入方程②.由此一来,二元化为一元了.
解得x=18. 把X=18代入y=22-x,得y=4,从而得到二元一次
方程组的解是 上面解方程组的基本思路是什么?主要步骤有哪些?基本思路:“消元”——把“二元”变为“一元”. 主要步骤:
将一个方程中的某个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,化二元一次方程组为一元一次方程.进而求得这个二元一次方程组的解.
这种方法叫做代入消元法,简称代入法.
例1 用代入法解方程组①
②解: 由①,得 x=y+3 ③
把③代入②,得 3(y+3)-8y=14.解这个方程,得 y= -1把y= -1代入③ ,得 x=2.所以这个方程组的解是分析:方程①中x的系数是1,用含y的式子表示x,比较简便.例2根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),
两种产品的销售数量比(按瓶计算)为2:5.某厂每天生产这种
消毒液22.5吨,这些消毒液应该分装大.小瓶装两种产品各
多少瓶?解:设这些消毒液应分装x大瓶和y小瓶.
由题意,得
①
②解这个方程,得 x= 20000.
把x= 20000代入③ ,得 y=50000.
所以这个方程组的解是
答:这个工厂一天应生产20000大瓶和50000小瓶消毒液.大瓶所装消毒液+小瓶所装消毒液=总生产量解(1) y=2x-3
(2) y=1-3x①
②解:把①代入②,得
3x+2(2x-3)=8.
3x+4x-6=8
7x=14
x=2
把x= 2代入① ,得 y=1.
所以这个方程组的解是
①
②解: 由①,得 y=2x-5 ③
把③代入②,得
3x+4(2x-5)=2.
解这个方程,得 x=2
把x= 2代入③ ,得 y=-1.
所以这个方程组的解是解:设有x支篮球队和y支排球队参赛.
由题意,得
①
②由①, 得 y =48- x ③
把③代入②,得 10x+12(48-x)=520
解这个方程,得 x= 28.
把x= 28代入③ ,得 y=20.
所以这个方程组的解是
P107解:设骑车用x小时,步行用y小时.
由题意,得
①
②由①, 得 y =1- x ③
把③代入②,得 25x+5(1-x)=20所以这个方程组的解是
本节课你有什么收获?1.解方程组的基本思路:“消元”——把“二元”变为“一元”.2.解方程组的方法:代入消元法.
