分类加法计数原理与分步乘法计数原理
文档属性
| 名称 | 分类加法计数原理与分步乘法计数原理 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-06 00:00:00 | ||
图片预览









文档简介
课件148张PPT。§ 1.1分类计数原理与分步计数原理思考? 用一个大写的的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?26+10=36问题 1. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。 一、分类计数原理 完成一件事,有n类办法. 在第1类办法中有m1种不同的方法,在第2类方法中有m2种不同的方法,……,在第n类方法中有mn种不同的方法,则完成这件事共有
2)首先要根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方法计数.1)各类办法之间相互独立,都能独立的完成这件事,要计算方法种数,只需将各类方法数相加,因此分类计数原理又称加法原理说明N= m1+m2+… + mn 种不同的方法
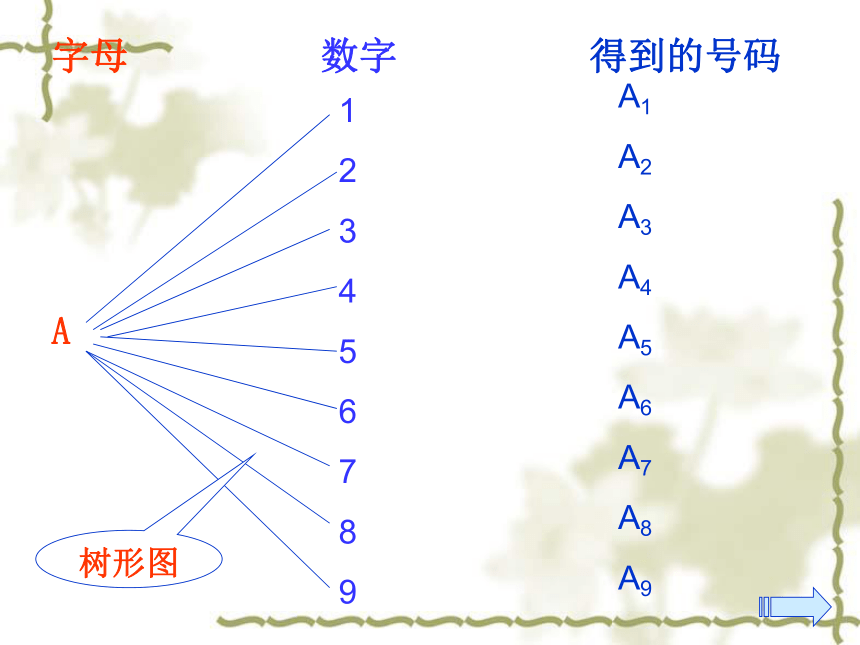
解:这名同学在A大学中有5种专业选择,在B大学中有4种专业选择。根据分类计数原理:这名同学可能的专业选择共有5+4=9种。 用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?思考? 分析:由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各个不同,因此共有6×9=54个不同的号码。字母 数字 得到的号码
A1
2
3
4
5
6
7
8
9A1
A2
A3
A4
A5
A6
A7
A8
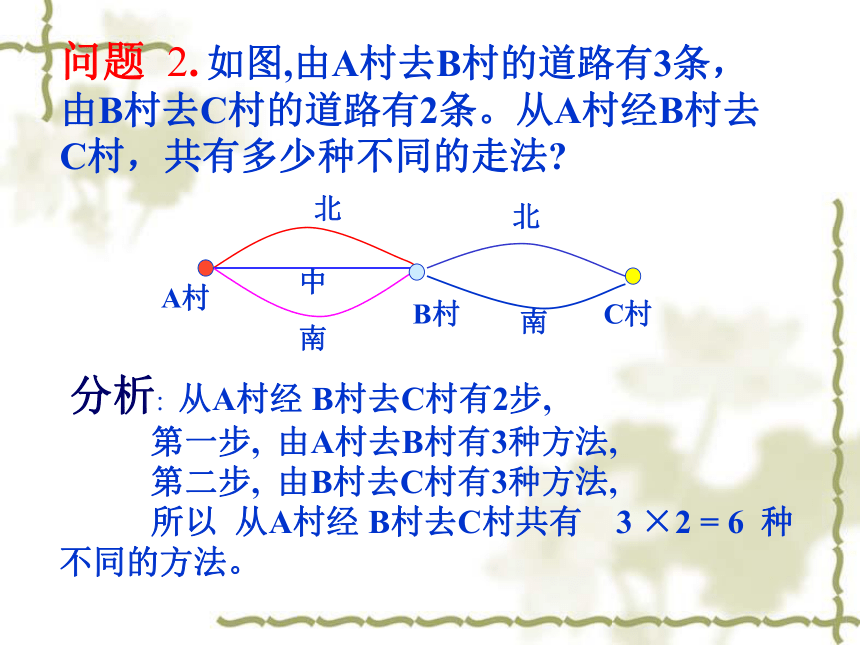
A9树形图问题 2. 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有3种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。二、分步计数原理 完成一件事,需要分成n个步骤。做第1步有m1种不同的方法,做第2步有m2种不同的方法, ……,做第n步有mn种不同的方法,则完成这件事共有
2)首先要根据具体问题的特点确定一个分步的标准,然后对每步方法计数.1)各个步骤相互依存,只有各个步骤都完成了,这件事才算完成,将各个步骤的方法数相乘得到完成这件事的方法总数,又称乘法原理说明N= m1×m2×… ×mn种不同的方法
如果完成一件事需要三个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,做第3步有m3种不同的方法,那么完成这件事共有
_________________种不同的方法.N=m1×m2×m3做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
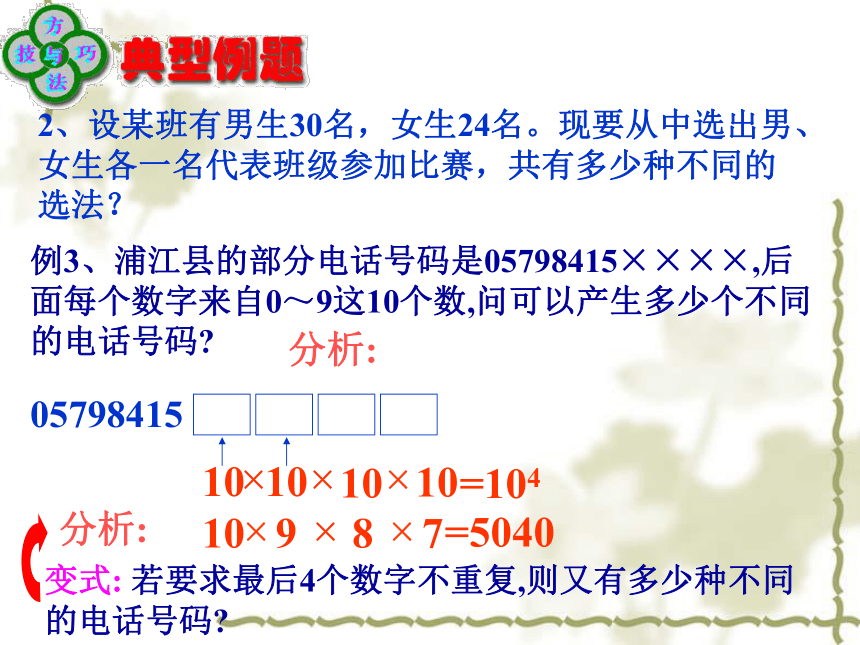
_____________________种不同的方法.N=m1×m2×…×mn 2、设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?例3、浦江县的部分电话号码是05798415××××,后面每个数字来自0~9这10个数,问可以产生多少个不同的电话号码?变式: 若要求最后4个数字不重复,则又有多少种不同的电话号码?05798415分析:分析:3、 书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育杂志.(2)从书架的第1、 2、 3层各取1本书,有多少种 不同取法? N=4+3+2=9 N=4 ×3×2=24(1)从书架上任取1本书,有多少种不同的取法?4、要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左右两边墙上的指定位置,问共有多少种不同的挂法?课堂练习1、在所有的两位数中,个位数字比十位数字大的两位数有多少个?2、8本不同的书,任选3本分给3个同学,每人1本,有多少种不同的分法?
3、将4封信投入3个不同的邮筒,有多少种不同的投法?
4、已知
则方程 可表示不同的圆的个数有多少?课堂练习5、已知二次函数 若
则可以得到多少个不同的二次函数?其中图象过原点的二次函数有多少个?图象过原点且顶点在第一象限的二次函数又有多少个?分类计数原理与分步计数原理有什么不同? 分类计数原理与分步计数原理都是涉及完成一件事的不同方法的种数的问题,它们的区别在于:
分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.分类加法与分步乘法计数原理的区别和联系:联系区别一完成一件事情共有n类
办法,关键词是“分类”完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成
这件事情。每一步得到的只是中间结果,
任何一步都不能能独立完成
这件事情,缺少任何一步也
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。
区别三各类办法是互斥的、
并列的、独立的各步之间是相关联的分类计数与分步计数原理的区别和联系:点评:乘法原理看成“串联电路”加法原理看成“并联电路”;如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?课堂练习N1=2×3=6N2=4×2=8N= N1+N2 =14 2.如图,该电路,从A到B共有多少条不同的线路可通电?AB分类完成分步完成解: 从总体上看由A到B的通电线路可分二类,
第一类, m1 = 4 条
第二类, m3 = 2×2 = 4, 条
所以, 根据加法原理, 从A到B共有
N = 4 + 4 = 8 条不同的线路可通电.解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4, 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
在解题有时既要分类又要分步。有60种取法。因此取法种数共有40+60=100(种)例1:
两个袋子里分别装有40个红球,60个白球,
从中任取一个球,有多少种求法?解:取一个球的方法可以分成两类:有40种取法;40个60个例2:
两个袋子里分别装有40个红球与60个白球,
从中取一个白球和一个红球,有多少种取法?60个40个解:取一个白球和一个红球可以分成两步
来完成:有60种取法;因此取一个白球和一个红球的方法共有60 ×40=2400(种)有40种取法。例3:
某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?解: (1) 完成从三好学生中任选一人去领奖这件事,共有2类办法,
第一类办法, 从男三好学生中任选一人, 共有 m1 = 5 种
不同的方法;
第二类办法, 从女三好学生中任选一人, 共有 m2 = 4 种不
同的方法;
所以, 根据加法原理, 得到不同选法种数共有
N = 5 + 4 = 9 种。
例3:
某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?解: (2) 完成从三好学生中任选男、女各一人去参加座谈会这件事, 需分2步完成,
第一步, 选一名男三好学生,有 m1 = 5 种方法;
第二步, 选一名女三好学生,有 m2 = 4 种方法;
所以, 不同选法种数共有 N = 5 × 4 = 20 种。
点评: 解题的关键是从总体上看这件事情是“分类完成”,还是“分步完成”,“分类完成”用“加法原理”,“分步完成”用“乘法原理”。
1、书架的第1层放有4本不同的计算机书,第2层放有3本不同
的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法? 4+3+2=9(种)4 ×3 ×2=24(种)2、由数字1,2,3,4,5,6可以组成多少个四位数?
(各位上的数字不重复)6 ×5 ×4 ×3=360(个)3、一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个
数字, 这4个拨号盘可以组成多少个四位数字的号码? 练习1 有些较复杂的问题往往不是单纯的“分类”“分步”可以解决的,而要将“分类”“分步”结合起来运用.一般是先“分类”,然后再在每一类中“分步”, 综合应用分类计数原理和分步计数原理.请看下面的例题: 注意例4:
某城市电话号码由8位组成,其中从左边算起的第1位只用
6或8,其余7位可以从前10个自然数0,1,2,…,9中任意
选取,允许数字重复。试问:该城市最多可装电话多少门?12345678第1类6解:装一门电话需要指定一个
电话号码,由题意电话号码可以
分成两类:第1类电话号码第1位用6,确定其余7位号码可以分7步完成。10101010101010因此第一类电话号码共有12345678第2类8实际问题 从甲地到乙地有3条路,从乙地到丁地有2条路;从甲地到丙地有3条路,从丙地到丁地有4条路,
问:从甲地到丁地有多少种走法?1.有不同的中文书9本,不同的英文书7本,不同的日文书5本.从其中取出不是同一国文字的书2本,问有多少种不同的取法?
2.集合A={1,2,-3},B={-1,-2,3,4} .从A,B 中各取1个元素作为点P(x,y) 的坐标.
(1)可以得到多少个不同的点?
(2)这些点中,位于第一象限的有几个?
3.某中学的一幢5层教学楼共有3处楼梯,问从1楼到5楼共有多少种不同的走法?
4.集合A={1,2,3,4},B={5,6,7}, 从A到B的映射有多少个?讲讲练练9×7+9×5+7×5=1433×4+4×3=242×2+2×2=83×3×3×3=813×3×3×3=81能否先排个位?法1:先排百位,然后十位,最后个位。奇偶解:在艺术组9人中,有且仅有一人既会钢琴又会小号(把该人称为“多面手”),只会钢琴的有6人,只会小号的有2人,把会钢琴、小号各1人的选法分为两类:
第一类:多面手入选,另一人只需从其他8人中任选一个,故这类选法共有8种.
第二类:多面手不入选,则会钢琴者只能从6个只会钢琴的人中选出,会小号的1人也只能从只会小号的 2人中选出,放这类选法共有6×2=12种,
故共有20种不同的选法.2.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?1.(1993年全国高考题)同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有(? )
(A)6种???? ?(B)9种???? (C)11种???????(D)23种2.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?作业:3.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?4、同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有(? )
(A)6种???? ?(B)9种???? (C)11种???????(D)23种何时用加法原理、乘法原理呢?加法原理完成一件事情有n类方法,若每一类方法中的任何一种方法均能将这件事情从头至尾完成.乘法原理完成一件事情有n个步骤,若每一步的任何一种方法只能完成这件事的一部分,并且必须且只需完成互相独立的这n步后,才能完成这件事.分类要做到“不重不漏”分步要做到“步骤完整”练习 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?分两步完成左边右边甲乙丙32第一步第二步× 在所有的两位数中,个位数字大于十位数字的两位数共有多少个? 分析1: 按个位数字是2,3,4,5,6,7,8,9分成8类,在每一类中满足条件的两位数分别是:
1个,2个,3个,4个,5个,6个,7 个,8 个.
根据加法原理共有 1+2+3+4+5+6+7+ 8 =36 (个).分析2: 按十位数字是1,2,3,4,5,6,7,8分成8类,在每一类中满足条件的两位数分别是:
8个,7个,6个,5个,4个,3个,2个,1个.
根据加法原理共有 8+7+6+5+4+3+2+1 = 36 (个)练习 一个三位密码锁,各位上数字由0,1,2,3,4,5, 6,7,8,9十个数字组成,可以设置多少种三位数的密码(各位上的数字允许重复)?首位数字不为0的密码数是多少?首位数字是0的密码数又是多少? 分析: 按密码位数,从左到右 依次设置第一位、第二位、第三 位, 需分为三步完成;
第一步, m1 = 10;
第二步, m2 = 10;
第三步, m3 = 10.
根据乘法原理, 共可以设置 N = 10×10×10 = 103 种三位数的密码。练习 答:首位数字不为0的密码数是 N =9×10×10 = 9×102 种,
首位数字是0的密码数是 N = 1×10×10 = 102 种。
由此可以看出, 首位数字不为0的密码数与首位数字是0的密码数之和等于密码总数。问: 若设置四位、五位、六位、…、十位等密码,密码数分别有多少种?答:它们的密码种数依次是 104 , 105, 106, …… 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习问: 若用2色、4色、5色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48, 5×4×3×3 = 180 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习 如图,一蚂蚁沿着长方体的棱,从一个顶点爬到相对的另一个顶点的最近路线共有多少条?练习 解:如图,从总体上看,如,蚂蚁从顶点A爬到顶点C1有三类方法,从局部上看每类又需两步完成,所以, 第一类, m1 = 1×2 = 2 条
第二类, m2 = 1×2 = 2 条
第三类, m3 = 1×2 = 2 条
所以, 根据加法原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。 例 有架楼梯共6级,每次只允许上一级或两级,求上完这架楼梯共有多少种不同的走法?第1类:走3步第2类:走4步第3类:走5步第4类:走6步N=1+6+5+1=13(种) 例:在1,2,3,…,200这些自然数中,各个数位上都不含数字8的自然数共有多少个?不含8的一位数
不含8的二位数
不含8的三位数N=8+72+82=162(个)例8.计算机编程人员在编写好程序以后要对
程序进行测试。程序员需要知道到底有多少
条执行路(即程序从开始到结束的线),以
便知道需要提供多少个测试数据。一般的,
一个程序模块又许多子模块组成,它的一个
具有许多执行路径的程序模块。问:这个程
序模块有多少条执行路径?另外为了减少测
试时间,程序员需要设法减少测试次数,你
能帮助程序员设计一个测试方式,以减少测
试次数吗?分析:整个模块的任意一条路径都分两步完成:
第1步是从开始执行到A点;第2步是从A点执行到结束。第一步可由子模块1或子模块2或子模块3来完成;
第二步可由子模块4或子模块5来完成。
因此,分析一条指令在整个模块的执行路径需要用到两个计数原理。解:由分类加法计数原理,
子模块 1 、2 、 3 中的子
路径共有
18 + 45 + 28 = 91 (条) ;
子模块 4 、 5 中的子路径
共有
38 + 43 = 81 (条) .
由分步乘法计数原理,
整个模块的执行路径共有
91×81 = 7 371(条). 2)在实际测试中,
程序员总是把每一个
子模块看成一个黑
箱,即通过只考察是
否执行了正确的子模
块的方式来测试整个
模块。这样,他可以
先分别单独测试5个
模块,以考察每个子
模块的工作是否正常。
总共需要的测试次数
为:18+45+28+38+43=172。再测试各个模块之间
的信息交流是否正
常,即第一步的子模
块与第二步的子模块
是否正常,需要测试
的次数为:3*2=6。
如果每个子模块都正
常工作,并且各个子
模块之间的信息交流
也正常,那么整个程
序模块就正常。这样,测试整个模块的次数就变为
172+6=178(次)用两个计数原理解决计数问题时,最重要的是在开始
计算之前要进行仔细分析 ,需要分类还是需要分步.
分类要做到“不重不漏”.
分类后再分别对每一类进行计数,最后用分类加
法计数原理求和,得到总数.
分步要做到“步骤完整” ―
完成了所有步骤,恰好完成任务,
当然步与步之间要相互独立.
分步后再计算每一步的方法数,
最后根据分步乘法计数原理,把完成每一步的方
法数相乘,得到总数.练习2、某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,共有多少种不同的进出商场的方式?1.由数字1,2,3,4,5,6可以组成没有重复数字的两位数的个数是( )
A.11 B.12
C.30 D.36
解析: 个位数字有6种选法,十位数字有5种选法,由分步乘法计数原理知,可组成6×5=30个无重复数字的两位数.
答案: C2.如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )
A.96 B.84
C.60 D.48
解析: 方法一:先种A地有4种,再种B地有3种,若C地与A地种相同的花,则C地有1种,D地有3种;若C地与A地种不同花,则C地有2种,D地有2种,即不同种法总数为N=4×3×(1×3+2×2)=84种.
方法二:若种4种花有4×3×2×1=24种;若种3种花,则A和C或B和D相同,有2×4×3×2=48种;若种2种花,则A和C相同且B和D相同,有4×3=12种.
共有N=24+48+12=84种.
答案: B3.三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过5次传递后,毽又被踢回给甲,则不同的传递方式共有________种.
解析: 如下图:
同理,甲传给丙也可以推出5种情况,综上有10种传法.
答案: 104.同室4人各写1张贺年卡,先集中起来,然后每人从中拿1张别人写的贺年卡,求4张贺年卡不同的分配方式有多少种?
解析: 方法一:对4人分别编1,2,3,4四个号,对四张贺年卡也编上1,2,3,4四个号,那么1,2,3,4四个数字填入1,2,3,4四个方格的一个填法对应贺卡的一个送法,原题转化为上面所述方格的编号与所填数字的不同的填法种数问题.首先,在1号方格里填数,可填上2,3,4中的任意一个数,有3种填法;其次,当在第1号方格填数i之后(2≤i≤4),在第i号方格中填上合乎要求的数,有3种填法;最后,将剩下的两个数,填到空着的方格里,只有1种填法合乎要求(因为这两个数中,至少有一个数与空的方格序号相同).
根据分步乘法计数原理,不同的分配方式共有3×3×1=9种.
方法二:21—4—33—4—14—1—3 31—4—241—22—1 41—2—331—22—1
共9种. 用0,1,2,3,4这五个数字可以组成多少个无重复数字的(1)四位密码?(2)四位数?(3)四位奇数?四位密码的首位可为0,四位数的首位不能为0,四位奇数的首位不为0且个位必须为奇数.[解题过程] (1)完成“组成无重复数字的四位密码”这件事,可以分为四步:第一步,选取左边第一个位置上的数字,有5种选取方法;第二步,选取左边第二个位置上的数字,有4种选取方法;第三步,选取左边第三个位置上的数字,有3种选取方法;第四步,选取左边第四个位置上的数字,有2种选取方法.由分步乘法计数原理,可以组成不同的四位密码共有N=5×4×3×2=120个.(2)完成“组成无重复数字的四位数”这件事,可以分四步:第一步,从1,2,3,4这4个数字中选一个数字作千位数字,共4种不同的选取方法,第二步从1,2,3,4中剩余的三个数字和0共4个数字选一个数字作百位数字,有4种不同的选取方法;第三步,从剩余的三个数字中选取一个数字作十位数字,有3种不同的选取方法;第四步,从剩余的两个数字中选取一个数字作个位数字,有2种不同的选取方法.由分步乘法计数原理,可以组成不同的四位数共有N=4×4×3×2=96个.(3)完成“组成无重复数字的四位奇数”这件事,可以分四步:
第一步定个位,只能从1、3中任取一个有两种方法,第二步定首位,把1、2、3、4中除去用过的一个还有3个可任取一个有3种方法,第三步,第四步把剩下的包括0在内的还有3个数字先排百位3种方法,再排十位有2种方法.由分步乘法计数原理共有2×3×3×2=36个.[题后感悟] (1)对于组数问题,一般按特殊位置(一般是末位和首位)由谁占领分类,分类中再按特殊位置(或者特殊元素)优先的方法分步完成;如果正面分类较多,可采用间接法从反面求解.
(2)解决组数问题,应特别注意其限制条件,有些条件是隐藏的,要善于挖掘.排数时,要注意特殊元素、特殊位置优先的原则.1.8张卡片上写着0,1,2,…,7共8个数字,取其中的三张卡片排放在一起,可组成多少个不同的三位数?
解析: 先排放百位从1,2,…,7共7个数中选一个有7种选法;再排十位,从除去百位的数外,剩余的7个数(包括0)中选一个,有7种选法;最后排个位,从除前两步选出的数外,剩余的6个数中选一个,有6种选法.由分步乘法计数原理,共可以组成7×7×6=294(个)不同的三位数. 用5种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,问有多少种不同的涂色方案?由题目可获取以下主要信息:
①用五种不同的颜色给四个区域涂色;
②相邻区域不能涂同种颜色;
③不相邻区域可以涂同种颜色.
解答本题可先给各个区域标上记号,从不相邻区域是否着相同颜色进行分类、分步解决.[解题过程] 先分为两类:
第一类,当D与A不同色,则可分为四步完成.第一步涂A有5种方法,第二步涂B有4种方法,第三步涂C有3种方法,第四步涂D有2种涂法,由分步乘法计数原理,共有5×4×3×2=120种方法.
第二类,当D与A同色,分三步完成,第一步涂A和D有5种方法,第二步涂B有4种方法,第三步涂C有3种方法,由分步乘法计数原理共有5×4×3=60(种),所以共有120+60=180种不同的方案.
[题后感悟] 染色问题是考查计数方法的一种常见问题,由于这类问题常常涉及分类与分步,所以在高考题中经常出现,处理这类问题的关键是要找准分类标准,像本题中A、D颜色是否相同对其他区域的涂色有影响. 2.如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?解析: 按地图A、B、C、D四个区域依次涂色,分四步完成:
第一步,涂A区域,有3种选择;
第二步,涂B区域,有2种选择;
第三步,涂C区域,由于它与A、B区域不同,有1种选择;
第四步,涂D区域,由于它与B、C区域不同,有1种选择.
所以根据分步乘法计数原理,得到不同的涂色方案种数共有3×2×1×1=6(种).3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种
解析: 从A开始,有6种方法,B有5种,C有4种,D、A种相同作物1种,D、A不同作物3种,
∴不同种法有6×5×4×(1+3)=480种.故选C.
答案: C 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?第(1)问属于分类的问题,用分类加法计数原理求解;第(2)问属于分步的问题,用分步乘法计数原理求解;第(3)问是综合类问题,要先分类再分步.[规范解答] (1)分三类:第一类,从高一年级选一人,有5种选择;第二类,从高二年级选一人,有6种选择;第三类,从高三年级选一人,有4种选择.由分类加法计数原理,共有5+6+4=15(种)选法.4分
(2)分三步完成:第一步,从高一年级选一人,有5种选择;第二步,从高二年级选一人,有6种选择;第三步,从高三年级选一人,有4种选择.由分步乘法计数原理,共有5×6×4=120(种)选法.8分
(3)分三类:高一、高二各一人,共有5×6=30(种)选法;高一、高三各一人,共有5×4=20(种)选法;高二、高三各一人,共有6×4=24(种)选法;由分类加法计数原理,共有30+20+24=74(种)选法.12分
[题后感悟] 使用两个原理解题的本质5.有一项活动,需在3名老师,8名男同学和5名女同学中选人参加.
(1)若只需一人参加,有多少种不同方法?
(2)若需老师、男同学、女同学各一人参加,有多少种不同选法?
(3)若需一名老师,一名学生参加,有多少种不同选法?3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?解析: (1)有三类选人的方法:3名老师中选一人,有3种方法;8名男同学中选一人,有8种方法,5名女同学中选一人,有5种方法.
由分类加法计数原理,共有3+8+5=16(种)选法.
(2)分三步选人:第一步选老师,有3种方法;第二步选男同学,有8种方法;第三步选女同学,有5种方法.由分步乘法计数原理,共有3×8×5=120(种)选法.
(3)可分两类,每一类又分两步.第一类,选一名老师再选一名男同学,有3×8=24(种)选法;第二类,选一名老师再选一名女同学,共有3×5=15(种)选法.
由分类加法计数原理,共有24+15=39(种)选法.◎有4种不同的作物可供选择种植在如图所示的4块试验田中,每块种植一种作物,相邻的试验田(有公共边)不能种植同一种作物,共有多少种不同的种植方法?【错解】 第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,种植C试验田有3种方法;
第四步,种植D试验田有2种方法;
由分步乘法计数原理知,共有N=4×3×3×2=72种种植方法.
【错因】 若按A、B、C、D的顺序依次种植作物,会导致D试验田的种植数受C试验田的影响,情况复杂.实际上种植C、D两块试验田再作为一步,用分类加法计数原理求解.【正解】 方法一:第一步,第二步与错解相同.
第三步,若C试验田种植的作物与B试验田相同,则D试验田有3种方法,此时有1×3=3种种植方法.
若C试验田种植的作物与B试验田不同,则C试验田有2种种植方法,D也有2种种植方法,共有2×2=4种种植方法.
由分类加法计数原理知,有3+4=7种方法.
第四步,由分步乘法计数原理有N=4×3×7=84种不同的种植方法.方法二:(1)若A、D种植同种作物,则A、D有4种不同的种法,B有3种种植方法,C也有3种种植方法,由分步乘法计数原理,共有4×3×3=36种种植方法.
(2)若A、D种植不同作物,则A有4种种植方法,D有3种种植方法,B有2种种植方法,C有2种种植方法,由分步乘法计数原理,共有4×3×2×2=48种种植方法.
综上所述,由分类加法计数原理,共有N=36+48=84种种植方法.
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。 一、分类计数原理 完成一件事,有n类办法. 在第1类办法中有m1种不同的方法,在第2类方法中有m2种不同的方法,……,在第n类方法中有mn种不同的方法,则完成这件事共有
2)首先要根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方法计数.1)各类办法之间相互独立,都能独立的完成这件事,要计算方法种数,只需将各类方法数相加,因此分类计数原理又称加法原理说明N= m1+m2+… + mn 种不同的方法
解:这名同学在A大学中有5种专业选择,在B大学中有4种专业选择。根据分类计数原理:这名同学可能的专业选择共有5+4=9种。 用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?思考? 分析:由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各个不同,因此共有6×9=54个不同的号码。字母 数字 得到的号码
A1
2
3
4
5
6
7
8
9A1
A2
A3
A4
A5
A6
A7
A8
A9树形图问题 2. 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有3种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。二、分步计数原理 完成一件事,需要分成n个步骤。做第1步有m1种不同的方法,做第2步有m2种不同的方法, ……,做第n步有mn种不同的方法,则完成这件事共有
2)首先要根据具体问题的特点确定一个分步的标准,然后对每步方法计数.1)各个步骤相互依存,只有各个步骤都完成了,这件事才算完成,将各个步骤的方法数相乘得到完成这件事的方法总数,又称乘法原理说明N= m1×m2×… ×mn种不同的方法
如果完成一件事需要三个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,做第3步有m3种不同的方法,那么完成这件事共有
_________________种不同的方法.N=m1×m2×m3做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
_____________________种不同的方法.N=m1×m2×…×mn 2、设某班有男生30名,女生24名。现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?例3、浦江县的部分电话号码是05798415××××,后面每个数字来自0~9这10个数,问可以产生多少个不同的电话号码?变式: 若要求最后4个数字不重复,则又有多少种不同的电话号码?05798415分析:分析:3、 书架上第1层放有4本不同的计算机书,第 2层放有3本不同的文艺书,第3层放有2本不同的体育杂志.(2)从书架的第1、 2、 3层各取1本书,有多少种 不同取法? N=4+3+2=9 N=4 ×3×2=24(1)从书架上任取1本书,有多少种不同的取法?4、要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左右两边墙上的指定位置,问共有多少种不同的挂法?课堂练习1、在所有的两位数中,个位数字比十位数字大的两位数有多少个?2、8本不同的书,任选3本分给3个同学,每人1本,有多少种不同的分法?
3、将4封信投入3个不同的邮筒,有多少种不同的投法?
4、已知
则方程 可表示不同的圆的个数有多少?课堂练习5、已知二次函数 若
则可以得到多少个不同的二次函数?其中图象过原点的二次函数有多少个?图象过原点且顶点在第一象限的二次函数又有多少个?分类计数原理与分步计数原理有什么不同? 分类计数原理与分步计数原理都是涉及完成一件事的不同方法的种数的问题,它们的区别在于:
分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.分类加法与分步乘法计数原理的区别和联系:联系区别一完成一件事情共有n类
办法,关键词是“分类”完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成
这件事情。每一步得到的只是中间结果,
任何一步都不能能独立完成
这件事情,缺少任何一步也
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。
区别三各类办法是互斥的、
并列的、独立的各步之间是相关联的分类计数与分步计数原理的区别和联系:点评:乘法原理看成“串联电路”加法原理看成“并联电路”;如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?课堂练习N1=2×3=6N2=4×2=8N= N1+N2 =14 2.如图,该电路,从A到B共有多少条不同的线路可通电?AB分类完成分步完成解: 从总体上看由A到B的通电线路可分二类,
第一类, m1 = 4 条
第二类, m3 = 2×2 = 4, 条
所以, 根据加法原理, 从A到B共有
N = 4 + 4 = 8 条不同的线路可通电.解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4, 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
在解题有时既要分类又要分步。有60种取法。因此取法种数共有40+60=100(种)例1:
两个袋子里分别装有40个红球,60个白球,
从中任取一个球,有多少种求法?解:取一个球的方法可以分成两类:有40种取法;40个60个例2:
两个袋子里分别装有40个红球与60个白球,
从中取一个白球和一个红球,有多少种取法?60个40个解:取一个白球和一个红球可以分成两步
来完成:有60种取法;因此取一个白球和一个红球的方法共有60 ×40=2400(种)有40种取法。例3:
某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?解: (1) 完成从三好学生中任选一人去领奖这件事,共有2类办法,
第一类办法, 从男三好学生中任选一人, 共有 m1 = 5 种
不同的方法;
第二类办法, 从女三好学生中任选一人, 共有 m2 = 4 种不
同的方法;
所以, 根据加法原理, 得到不同选法种数共有
N = 5 + 4 = 9 种。
例3:
某班级有男三好学生5人,女三好学生4人。
(1)从中任选一人去领奖, 有多少种不同的选法?
(2) 从中任选男、女三好学生各一人去参加座谈会,有多少种不同的选法?解: (2) 完成从三好学生中任选男、女各一人去参加座谈会这件事, 需分2步完成,
第一步, 选一名男三好学生,有 m1 = 5 种方法;
第二步, 选一名女三好学生,有 m2 = 4 种方法;
所以, 不同选法种数共有 N = 5 × 4 = 20 种。
点评: 解题的关键是从总体上看这件事情是“分类完成”,还是“分步完成”,“分类完成”用“加法原理”,“分步完成”用“乘法原理”。
1、书架的第1层放有4本不同的计算机书,第2层放有3本不同
的文艺书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法? 4+3+2=9(种)4 ×3 ×2=24(种)2、由数字1,2,3,4,5,6可以组成多少个四位数?
(各位上的数字不重复)6 ×5 ×4 ×3=360(个)3、一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个
数字, 这4个拨号盘可以组成多少个四位数字的号码? 练习1 有些较复杂的问题往往不是单纯的“分类”“分步”可以解决的,而要将“分类”“分步”结合起来运用.一般是先“分类”,然后再在每一类中“分步”, 综合应用分类计数原理和分步计数原理.请看下面的例题: 注意例4:
某城市电话号码由8位组成,其中从左边算起的第1位只用
6或8,其余7位可以从前10个自然数0,1,2,…,9中任意
选取,允许数字重复。试问:该城市最多可装电话多少门?12345678第1类6解:装一门电话需要指定一个
电话号码,由题意电话号码可以
分成两类:第1类电话号码第1位用6,确定其余7位号码可以分7步完成。10101010101010因此第一类电话号码共有12345678第2类8实际问题 从甲地到乙地有3条路,从乙地到丁地有2条路;从甲地到丙地有3条路,从丙地到丁地有4条路,
问:从甲地到丁地有多少种走法?1.有不同的中文书9本,不同的英文书7本,不同的日文书5本.从其中取出不是同一国文字的书2本,问有多少种不同的取法?
2.集合A={1,2,-3},B={-1,-2,3,4} .从A,B 中各取1个元素作为点P(x,y) 的坐标.
(1)可以得到多少个不同的点?
(2)这些点中,位于第一象限的有几个?
3.某中学的一幢5层教学楼共有3处楼梯,问从1楼到5楼共有多少种不同的走法?
4.集合A={1,2,3,4},B={5,6,7}, 从A到B的映射有多少个?讲讲练练9×7+9×5+7×5=1433×4+4×3=242×2+2×2=83×3×3×3=813×3×3×3=81能否先排个位?法1:先排百位,然后十位,最后个位。奇偶解:在艺术组9人中,有且仅有一人既会钢琴又会小号(把该人称为“多面手”),只会钢琴的有6人,只会小号的有2人,把会钢琴、小号各1人的选法分为两类:
第一类:多面手入选,另一人只需从其他8人中任选一个,故这类选法共有8种.
第二类:多面手不入选,则会钢琴者只能从6个只会钢琴的人中选出,会小号的1人也只能从只会小号的 2人中选出,放这类选法共有6×2=12种,
故共有20种不同的选法.2.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?1.(1993年全国高考题)同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有(? )
(A)6种???? ?(B)9种???? (C)11种???????(D)23种2.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?作业:3.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?4、同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有(? )
(A)6种???? ?(B)9种???? (C)11种???????(D)23种何时用加法原理、乘法原理呢?加法原理完成一件事情有n类方法,若每一类方法中的任何一种方法均能将这件事情从头至尾完成.乘法原理完成一件事情有n个步骤,若每一步的任何一种方法只能完成这件事的一部分,并且必须且只需完成互相独立的这n步后,才能完成这件事.分类要做到“不重不漏”分步要做到“步骤完整”练习 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法?分两步完成左边右边甲乙丙32第一步第二步× 在所有的两位数中,个位数字大于十位数字的两位数共有多少个? 分析1: 按个位数字是2,3,4,5,6,7,8,9分成8类,在每一类中满足条件的两位数分别是:
1个,2个,3个,4个,5个,6个,7 个,8 个.
根据加法原理共有 1+2+3+4+5+6+7+ 8 =36 (个).分析2: 按十位数字是1,2,3,4,5,6,7,8分成8类,在每一类中满足条件的两位数分别是:
8个,7个,6个,5个,4个,3个,2个,1个.
根据加法原理共有 8+7+6+5+4+3+2+1 = 36 (个)练习 一个三位密码锁,各位上数字由0,1,2,3,4,5, 6,7,8,9十个数字组成,可以设置多少种三位数的密码(各位上的数字允许重复)?首位数字不为0的密码数是多少?首位数字是0的密码数又是多少? 分析: 按密码位数,从左到右 依次设置第一位、第二位、第三 位, 需分为三步完成;
第一步, m1 = 10;
第二步, m2 = 10;
第三步, m3 = 10.
根据乘法原理, 共可以设置 N = 10×10×10 = 103 种三位数的密码。练习 答:首位数字不为0的密码数是 N =9×10×10 = 9×102 种,
首位数字是0的密码数是 N = 1×10×10 = 102 种。
由此可以看出, 首位数字不为0的密码数与首位数字是0的密码数之和等于密码总数。问: 若设置四位、五位、六位、…、十位等密码,密码数分别有多少种?答:它们的密码种数依次是 104 , 105, 106, …… 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习问: 若用2色、4色、5色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48, 5×4×3×3 = 180 种。 如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?练习 如图,一蚂蚁沿着长方体的棱,从一个顶点爬到相对的另一个顶点的最近路线共有多少条?练习 解:如图,从总体上看,如,蚂蚁从顶点A爬到顶点C1有三类方法,从局部上看每类又需两步完成,所以, 第一类, m1 = 1×2 = 2 条
第二类, m2 = 1×2 = 2 条
第三类, m3 = 1×2 = 2 条
所以, 根据加法原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。 例 有架楼梯共6级,每次只允许上一级或两级,求上完这架楼梯共有多少种不同的走法?第1类:走3步第2类:走4步第3类:走5步第4类:走6步N=1+6+5+1=13(种) 例:在1,2,3,…,200这些自然数中,各个数位上都不含数字8的自然数共有多少个?不含8的一位数
不含8的二位数
不含8的三位数N=8+72+82=162(个)例8.计算机编程人员在编写好程序以后要对
程序进行测试。程序员需要知道到底有多少
条执行路(即程序从开始到结束的线),以
便知道需要提供多少个测试数据。一般的,
一个程序模块又许多子模块组成,它的一个
具有许多执行路径的程序模块。问:这个程
序模块有多少条执行路径?另外为了减少测
试时间,程序员需要设法减少测试次数,你
能帮助程序员设计一个测试方式,以减少测
试次数吗?分析:整个模块的任意一条路径都分两步完成:
第1步是从开始执行到A点;第2步是从A点执行到结束。第一步可由子模块1或子模块2或子模块3来完成;
第二步可由子模块4或子模块5来完成。
因此,分析一条指令在整个模块的执行路径需要用到两个计数原理。解:由分类加法计数原理,
子模块 1 、2 、 3 中的子
路径共有
18 + 45 + 28 = 91 (条) ;
子模块 4 、 5 中的子路径
共有
38 + 43 = 81 (条) .
由分步乘法计数原理,
整个模块的执行路径共有
91×81 = 7 371(条). 2)在实际测试中,
程序员总是把每一个
子模块看成一个黑
箱,即通过只考察是
否执行了正确的子模
块的方式来测试整个
模块。这样,他可以
先分别单独测试5个
模块,以考察每个子
模块的工作是否正常。
总共需要的测试次数
为:18+45+28+38+43=172。再测试各个模块之间
的信息交流是否正
常,即第一步的子模
块与第二步的子模块
是否正常,需要测试
的次数为:3*2=6。
如果每个子模块都正
常工作,并且各个子
模块之间的信息交流
也正常,那么整个程
序模块就正常。这样,测试整个模块的次数就变为
172+6=178(次)用两个计数原理解决计数问题时,最重要的是在开始
计算之前要进行仔细分析 ,需要分类还是需要分步.
分类要做到“不重不漏”.
分类后再分别对每一类进行计数,最后用分类加
法计数原理求和,得到总数.
分步要做到“步骤完整” ―
完成了所有步骤,恰好完成任务,
当然步与步之间要相互独立.
分步后再计算每一步的方法数,
最后根据分步乘法计数原理,把完成每一步的方
法数相乘,得到总数.练习2、某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,共有多少种不同的进出商场的方式?1.由数字1,2,3,4,5,6可以组成没有重复数字的两位数的个数是( )
A.11 B.12
C.30 D.36
解析: 个位数字有6种选法,十位数字有5种选法,由分步乘法计数原理知,可组成6×5=30个无重复数字的两位数.
答案: C2.如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )
A.96 B.84
C.60 D.48
解析: 方法一:先种A地有4种,再种B地有3种,若C地与A地种相同的花,则C地有1种,D地有3种;若C地与A地种不同花,则C地有2种,D地有2种,即不同种法总数为N=4×3×(1×3+2×2)=84种.
方法二:若种4种花有4×3×2×1=24种;若种3种花,则A和C或B和D相同,有2×4×3×2=48种;若种2种花,则A和C相同且B和D相同,有4×3=12种.
共有N=24+48+12=84种.
答案: B3.三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过5次传递后,毽又被踢回给甲,则不同的传递方式共有________种.
解析: 如下图:
同理,甲传给丙也可以推出5种情况,综上有10种传法.
答案: 104.同室4人各写1张贺年卡,先集中起来,然后每人从中拿1张别人写的贺年卡,求4张贺年卡不同的分配方式有多少种?
解析: 方法一:对4人分别编1,2,3,4四个号,对四张贺年卡也编上1,2,3,4四个号,那么1,2,3,4四个数字填入1,2,3,4四个方格的一个填法对应贺卡的一个送法,原题转化为上面所述方格的编号与所填数字的不同的填法种数问题.首先,在1号方格里填数,可填上2,3,4中的任意一个数,有3种填法;其次,当在第1号方格填数i之后(2≤i≤4),在第i号方格中填上合乎要求的数,有3种填法;最后,将剩下的两个数,填到空着的方格里,只有1种填法合乎要求(因为这两个数中,至少有一个数与空的方格序号相同).
根据分步乘法计数原理,不同的分配方式共有3×3×1=9种.
方法二:21—4—33—4—14—1—3 31—4—241—22—1 41—2—331—22—1
共9种. 用0,1,2,3,4这五个数字可以组成多少个无重复数字的(1)四位密码?(2)四位数?(3)四位奇数?四位密码的首位可为0,四位数的首位不能为0,四位奇数的首位不为0且个位必须为奇数.[解题过程] (1)完成“组成无重复数字的四位密码”这件事,可以分为四步:第一步,选取左边第一个位置上的数字,有5种选取方法;第二步,选取左边第二个位置上的数字,有4种选取方法;第三步,选取左边第三个位置上的数字,有3种选取方法;第四步,选取左边第四个位置上的数字,有2种选取方法.由分步乘法计数原理,可以组成不同的四位密码共有N=5×4×3×2=120个.(2)完成“组成无重复数字的四位数”这件事,可以分四步:第一步,从1,2,3,4这4个数字中选一个数字作千位数字,共4种不同的选取方法,第二步从1,2,3,4中剩余的三个数字和0共4个数字选一个数字作百位数字,有4种不同的选取方法;第三步,从剩余的三个数字中选取一个数字作十位数字,有3种不同的选取方法;第四步,从剩余的两个数字中选取一个数字作个位数字,有2种不同的选取方法.由分步乘法计数原理,可以组成不同的四位数共有N=4×4×3×2=96个.(3)完成“组成无重复数字的四位奇数”这件事,可以分四步:
第一步定个位,只能从1、3中任取一个有两种方法,第二步定首位,把1、2、3、4中除去用过的一个还有3个可任取一个有3种方法,第三步,第四步把剩下的包括0在内的还有3个数字先排百位3种方法,再排十位有2种方法.由分步乘法计数原理共有2×3×3×2=36个.[题后感悟] (1)对于组数问题,一般按特殊位置(一般是末位和首位)由谁占领分类,分类中再按特殊位置(或者特殊元素)优先的方法分步完成;如果正面分类较多,可采用间接法从反面求解.
(2)解决组数问题,应特别注意其限制条件,有些条件是隐藏的,要善于挖掘.排数时,要注意特殊元素、特殊位置优先的原则.1.8张卡片上写着0,1,2,…,7共8个数字,取其中的三张卡片排放在一起,可组成多少个不同的三位数?
解析: 先排放百位从1,2,…,7共7个数中选一个有7种选法;再排十位,从除去百位的数外,剩余的7个数(包括0)中选一个,有7种选法;最后排个位,从除前两步选出的数外,剩余的6个数中选一个,有6种选法.由分步乘法计数原理,共可以组成7×7×6=294(个)不同的三位数. 用5种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,问有多少种不同的涂色方案?由题目可获取以下主要信息:
①用五种不同的颜色给四个区域涂色;
②相邻区域不能涂同种颜色;
③不相邻区域可以涂同种颜色.
解答本题可先给各个区域标上记号,从不相邻区域是否着相同颜色进行分类、分步解决.[解题过程] 先分为两类:
第一类,当D与A不同色,则可分为四步完成.第一步涂A有5种方法,第二步涂B有4种方法,第三步涂C有3种方法,第四步涂D有2种涂法,由分步乘法计数原理,共有5×4×3×2=120种方法.
第二类,当D与A同色,分三步完成,第一步涂A和D有5种方法,第二步涂B有4种方法,第三步涂C有3种方法,由分步乘法计数原理共有5×4×3=60(种),所以共有120+60=180种不同的方案.
[题后感悟] 染色问题是考查计数方法的一种常见问题,由于这类问题常常涉及分类与分步,所以在高考题中经常出现,处理这类问题的关键是要找准分类标准,像本题中A、D颜色是否相同对其他区域的涂色有影响. 2.如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?解析: 按地图A、B、C、D四个区域依次涂色,分四步完成:
第一步,涂A区域,有3种选择;
第二步,涂B区域,有2种选择;
第三步,涂C区域,由于它与A、B区域不同,有1种选择;
第四步,涂D区域,由于它与B、C区域不同,有1种选择.
所以根据分步乘法计数原理,得到不同的涂色方案种数共有3×2×1×1=6(种).3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种
解析: 从A开始,有6种方法,B有5种,C有4种,D、A种相同作物1种,D、A不同作物3种,
∴不同种法有6×5×4×(1+3)=480种.故选C.
答案: C 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?第(1)问属于分类的问题,用分类加法计数原理求解;第(2)问属于分步的问题,用分步乘法计数原理求解;第(3)问是综合类问题,要先分类再分步.[规范解答] (1)分三类:第一类,从高一年级选一人,有5种选择;第二类,从高二年级选一人,有6种选择;第三类,从高三年级选一人,有4种选择.由分类加法计数原理,共有5+6+4=15(种)选法.4分
(2)分三步完成:第一步,从高一年级选一人,有5种选择;第二步,从高二年级选一人,有6种选择;第三步,从高三年级选一人,有4种选择.由分步乘法计数原理,共有5×6×4=120(种)选法.8分
(3)分三类:高一、高二各一人,共有5×6=30(种)选法;高一、高三各一人,共有5×4=20(种)选法;高二、高三各一人,共有6×4=24(种)选法;由分类加法计数原理,共有30+20+24=74(种)选法.12分
[题后感悟] 使用两个原理解题的本质5.有一项活动,需在3名老师,8名男同学和5名女同学中选人参加.
(1)若只需一人参加,有多少种不同方法?
(2)若需老师、男同学、女同学各一人参加,有多少种不同选法?
(3)若需一名老师,一名学生参加,有多少种不同选法?3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?3. 用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种. 因此应先分类后分步.
第一类,B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法. 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.由题目可获取以下主要信息:
①从四种蔬菜品种选出3种分别种在不同土质的三块土地上;
②黄瓜必须种植.
解答此题可考虑以黄瓜所种植的土地分类求解或用间接法求解.[解题过程] 方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.[题后感悟] 对于同一个事件的处理,往往可以采用不同的处理方法,从而得到不同的解法,但结果肯定是相同的,用这种方法可以起到很好的检验效果.
按元素性质分类,按事件发生过程分步是计数问题的基本思想方法,区分“分类”与“分步”的关键,是验证你提供的某一种方法是否完成了这件事情,分类中的每一种方法都完成了这件事情,而分步中的每一种方法不能完成这件事情,只是向事情的完成迈进了一步. 4.如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种 D.496种 某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?解析: (1)有三类选人的方法:3名老师中选一人,有3种方法;8名男同学中选一人,有8种方法,5名女同学中选一人,有5种方法.
由分类加法计数原理,共有3+8+5=16(种)选法.
(2)分三步选人:第一步选老师,有3种方法;第二步选男同学,有8种方法;第三步选女同学,有5种方法.由分步乘法计数原理,共有3×8×5=120(种)选法.
(3)可分两类,每一类又分两步.第一类,选一名老师再选一名男同学,有3×8=24(种)选法;第二类,选一名老师再选一名女同学,共有3×5=15(种)选法.
由分类加法计数原理,共有24+15=39(种)选法.◎有4种不同的作物可供选择种植在如图所示的4块试验田中,每块种植一种作物,相邻的试验田(有公共边)不能种植同一种作物,共有多少种不同的种植方法?【错解】 第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,种植C试验田有3种方法;
第四步,种植D试验田有2种方法;
由分步乘法计数原理知,共有N=4×3×3×2=72种种植方法.
【错因】 若按A、B、C、D的顺序依次种植作物,会导致D试验田的种植数受C试验田的影响,情况复杂.实际上种植C、D两块试验田再作为一步,用分类加法计数原理求解.【正解】 方法一:第一步,第二步与错解相同.
第三步,若C试验田种植的作物与B试验田相同,则D试验田有3种方法,此时有1×3=3种种植方法.
若C试验田种植的作物与B试验田不同,则C试验田有2种种植方法,D也有2种种植方法,共有2×2=4种种植方法.
由分类加法计数原理知,有3+4=7种方法.
第四步,由分步乘法计数原理有N=4×3×7=84种不同的种植方法.方法二:(1)若A、D种植同种作物,则A、D有4种不同的种法,B有3种种植方法,C也有3种种植方法,由分步乘法计数原理,共有4×3×3=36种种植方法.
(2)若A、D种植不同作物,则A有4种种植方法,D有3种种植方法,B有2种种植方法,C有2种种植方法,由分步乘法计数原理,共有4×3×2×2=48种种植方法.
综上所述,由分类加法计数原理,共有N=36+48=84种种植方法.
