7.8 机械能守恒定律
图片预览


文档简介
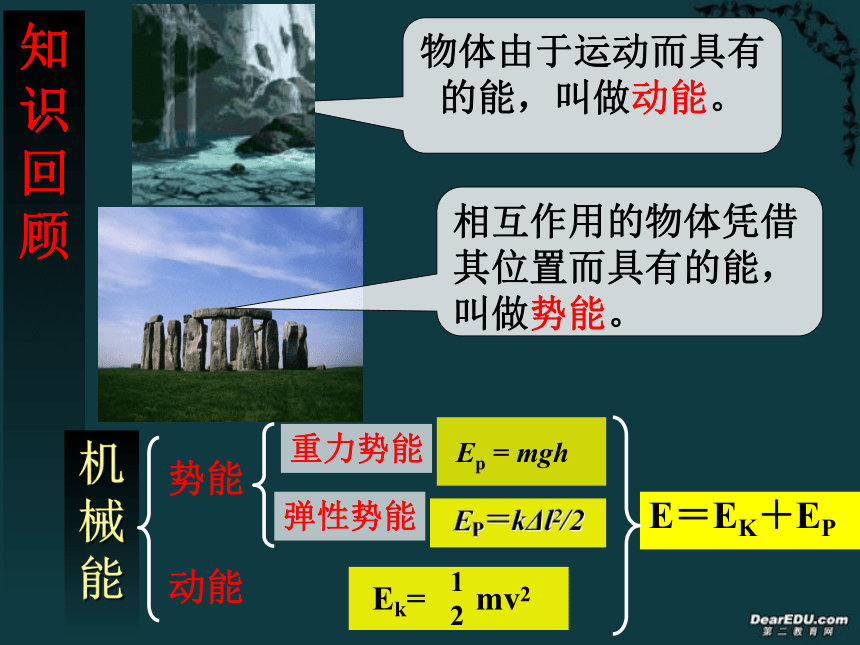
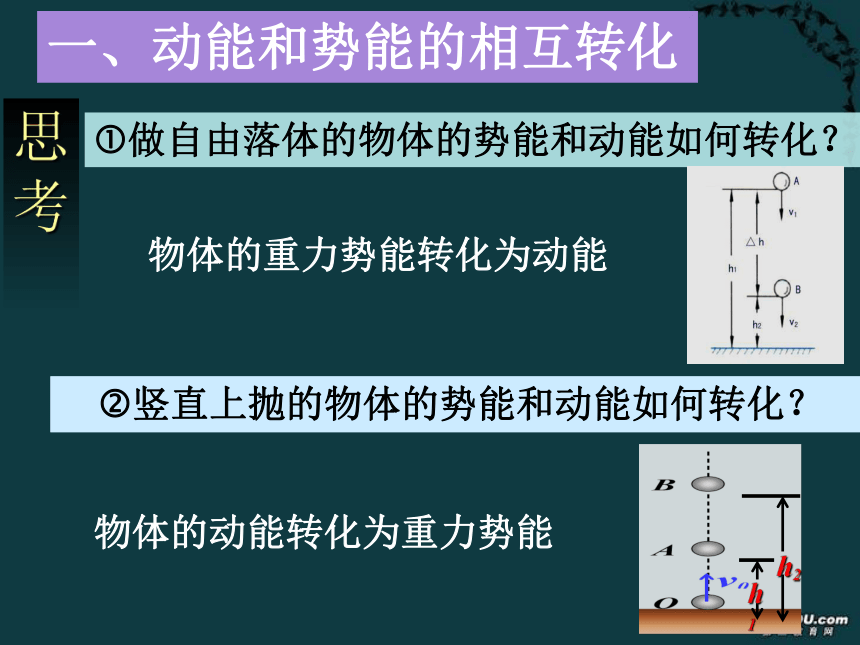
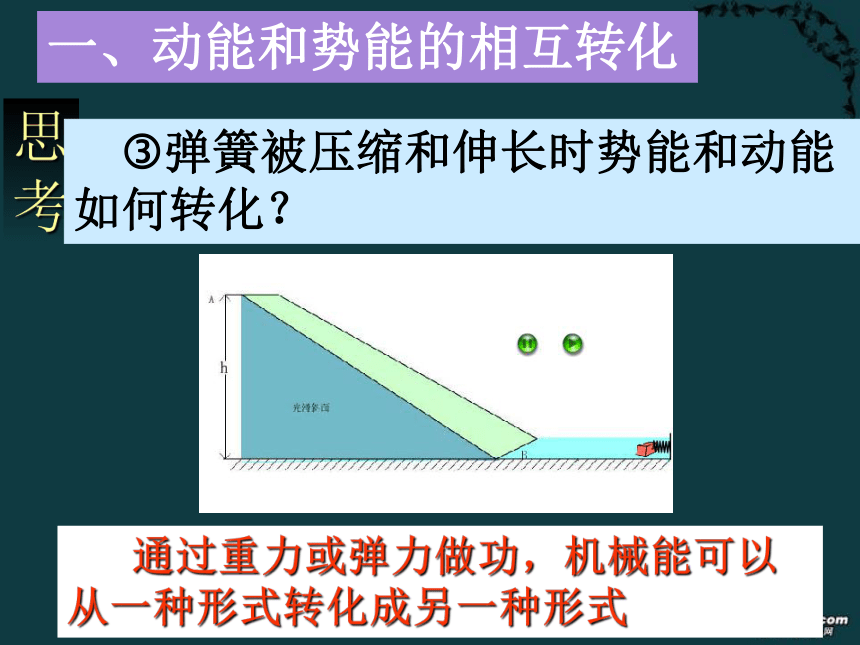
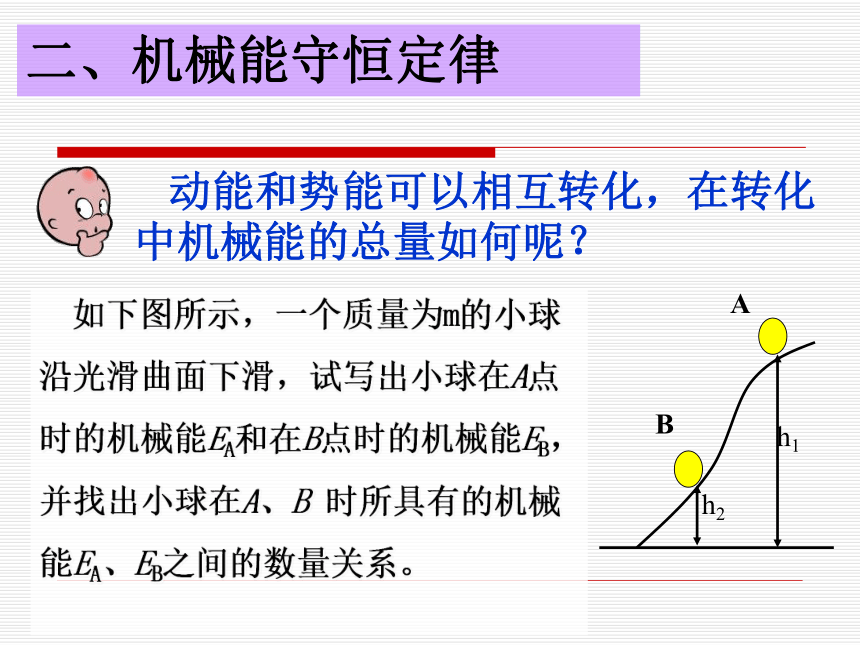
课件20张PPT。知识回顾相互作用的物体凭借其位置而具有的能,叫做势能。物体由于运动而具有的能,叫做动能。机械能势能动能重力势能弹性势能 Ep = mgh EP=kΔl2/2E=EK+EPE=EK+EP机械能理解:(1)机械能是标量,但有正、负(因重力势能有正、负)(2)机械能具有相对性,因为势能具有相对性(须确定零势能参考平面)同时,与动能相关的速度也具有相对性(一般以地面为参考系)所以机械能也具有相对性。 只有在确定参考系和零势能参考平面的情况下,机械能才有确定 物理意义。?做自由落体的物体的势能和动能如何转化?思考物体的重力势能转化为动能一、动能和势能的相互转化 ?竖直上抛的物体的势能和动能如何转化?物体的动能转化为重力势能思考一、动能和势能的相互转化 ?弹簧被压缩和伸长时势能和动能如何转化? 通过重力或弹力做功,机械能可以从一种形式转化成另一种形式二、机械能守恒定律 动能和势能可以相互转化,在转化中机械能的总量如何呢? 如下图所示,一个质量为m的小球
沿光滑曲面下滑,试写出小球在A点
时的机械能EA和在B点时的机械能EB,
并找出小球在A、B 时所具有的机械
能EA、EB之间的数量关系。
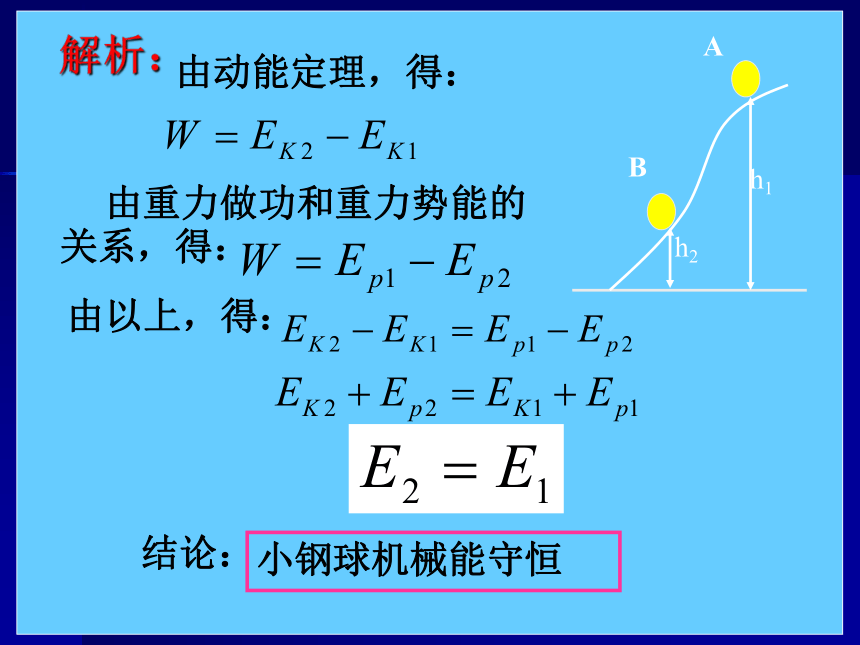
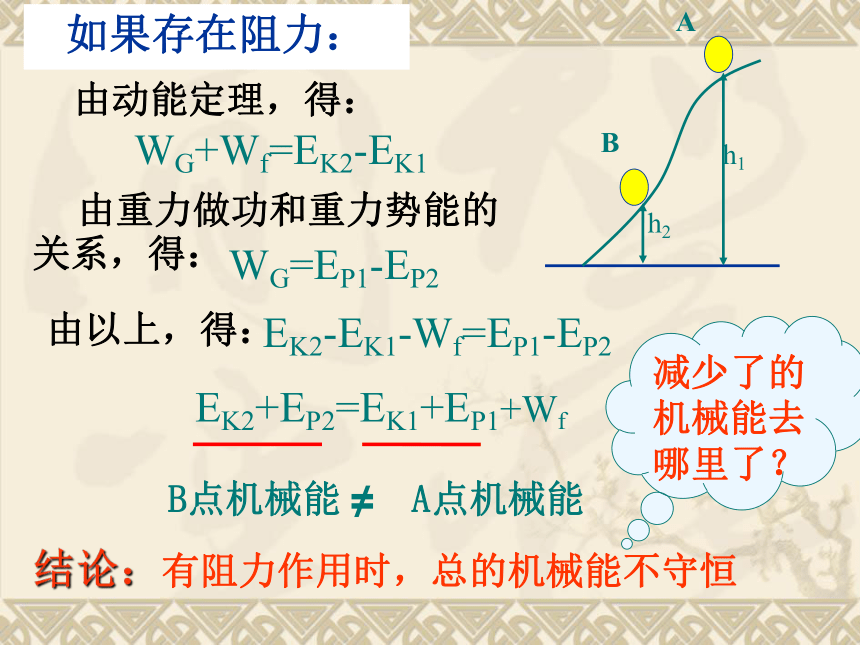
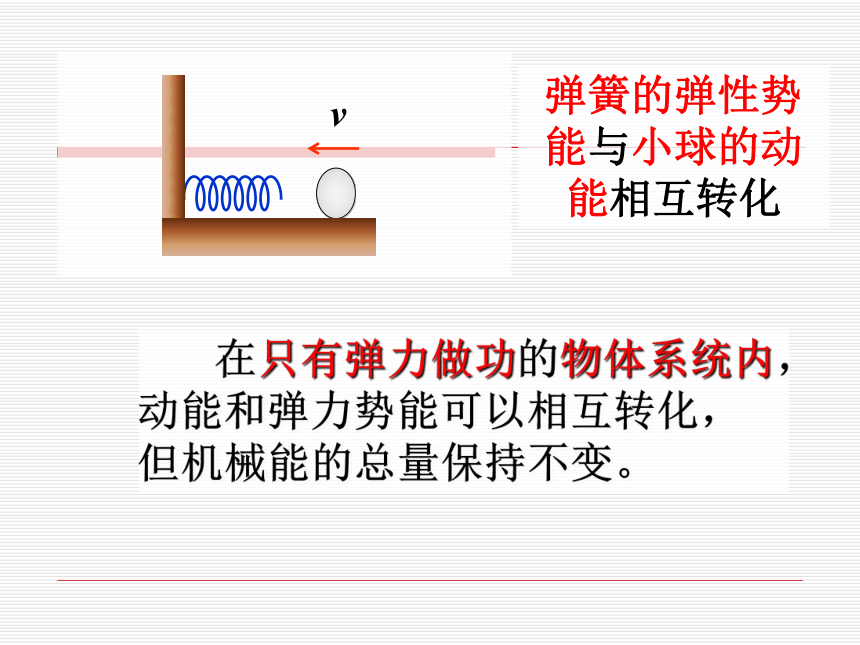
由动能定理,得:小钢球机械能守恒 由重力做功和重力势能的关系,得:由以上,得:结论:解析:如果存在阻力:WG+Wf=EK2-EK1由动能定理,得: 由重力做功和重力势能的关系,得:WG=EP1-EP2由以上,得:EK2-EK1-Wf=EP1-EP2EK2+EP2=EK1+EP1+WfB点机械能A点机械能≠结论:有阻力作用时,总的机械能不守恒减少了的机械能去哪里了? 在只有弹力做功的物体系统内,动能和弹力势能可以相互转化,但机械能的总量保持不变。弹簧的弹性势能与小球的动能相互转化 在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,总的机械能保持不变。1、内容E2=E1 即 EK2+EP2=EK1+EP1ΔEk= -ΔEp2、表达式即 EK2-EK1=EP1 -EP2 二、机械能守恒定律 在只有重力或弹力做功的物体系统内3、条件(1)从系统做功的角度:只有重力或弹力做功。机械能守恒定律的条件的理解:(2)从能量转化的角度:只有系统内的动能和势能相互转化,无其他形式能量(如内能)参与转化。物体只受重力;②物体除受重力外还受其他的力,
但其他力不做功; ③物体除受重力外还受其他的力,
但其他力做功的代数和为零例1.下列实例(均不计空气阻力)中的运动物体,机械能守恒的是( )
A.被起重机吊起的货物正在加速上升
B.斜抛出去的小球
C.木块沿粗糙斜面匀速下滑
D.光滑水平面上,一个轻质弹簧左端固定,右端连接一小球,沿水平方向做振动的小球 B例2. 忽略一切阻力,如图。摆长为L,最大偏角为θ。小球运动到最低位置时的速度是多大?由机械能守恒定律得即得末状态解:选O所在平面为零势能面初状态 总结:应用机械能守恒定律解题步骤(4)根据机械能守恒定律列出方程,进行求解。(1)确定研究对象和研究过程(2)分析研究对象在运动过程中的受力情况弄清各力做功的情况,判断机械能是否守恒(3) 恰当选取零势能面,并确定研究对象在研究过程的始、末状态的机械能。 【课堂练习】
1.下列实例中的运动物体,哪些机械能不守恒( )
A.跳伞运动员在空中匀速下降
B.滑雪运动员自高坡顶上自由下滑(不计空气阻力和摩擦)
C.汽车在水平路面上匀速行驶
D.集装箱被吊车匀速地吊起(空气阻力不计)AD 2. 如图所示,木块在固定的斜面上运动,其中图C中的斜面是光滑的,图A、B、D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示,大小与摩擦阻力相等,图A、B、D中的木块向下运动,图C中的木块向上运动.在这四个图所示的运动过程中机械能守恒的是( )AC 3、如图所示,轻弹簧下端挂一质量为m的物体,另一端悬挂于O点,现将物体拉到与悬点等高的位置并保持弹簧处于原长状态,放手后物体向下运动.在运动到悬点O正下方的过程中,下列说法正确的是( )
A.物体和地球组成的系统机械能守恒
B.物体和地球组成的系统机械能在减少
C.物体、地球和弹簧三者
组成的系统机械能守恒
D.全过程的初、末状态相比,
重力势能和弹性势能之和增加了C 4.如图所示,轻质弹簧的一端与墙相连,质量为2kg的滑块以5m/s的初速度沿光滑平面运动并压缩弹簧,求:
(1)弹簧在被压缩过程中最大弹性势能.
(2)当木块的速度减为2 m/s时,弹簧具有的弹性势能.(1)由ΔEk= -ΔEp知Ep=25J(2)由EK2-EK1=EP1 -EP2 知
EP2=21J解: 课后拓展
如图所示.一根长L的细绳,固定在O点,绳另一端系一条质量为m的小球.起初将小球拉至水平于A点.求:
(1)小球从A点由静止释放后到达最低点C时的速度。 (2)小球摆到最低点时细绳的拉力。 解:(1)由机械能守恒有:(2) 在最低点,根据牛顿第二定律:解得:有:T-mg=mv2/L解得:T=3mg谢谢!
沿光滑曲面下滑,试写出小球在A点
时的机械能EA和在B点时的机械能EB,
并找出小球在A、B 时所具有的机械
能EA、EB之间的数量关系。
由动能定理,得:小钢球机械能守恒 由重力做功和重力势能的关系,得:由以上,得:结论:解析:如果存在阻力:WG+Wf=EK2-EK1由动能定理,得: 由重力做功和重力势能的关系,得:WG=EP1-EP2由以上,得:EK2-EK1-Wf=EP1-EP2EK2+EP2=EK1+EP1+WfB点机械能A点机械能≠结论:有阻力作用时,总的机械能不守恒减少了的机械能去哪里了? 在只有弹力做功的物体系统内,动能和弹力势能可以相互转化,但机械能的总量保持不变。弹簧的弹性势能与小球的动能相互转化 在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,总的机械能保持不变。1、内容E2=E1 即 EK2+EP2=EK1+EP1ΔEk= -ΔEp2、表达式即 EK2-EK1=EP1 -EP2 二、机械能守恒定律 在只有重力或弹力做功的物体系统内3、条件(1)从系统做功的角度:只有重力或弹力做功。机械能守恒定律的条件的理解:(2)从能量转化的角度:只有系统内的动能和势能相互转化,无其他形式能量(如内能)参与转化。物体只受重力;②物体除受重力外还受其他的力,
但其他力不做功; ③物体除受重力外还受其他的力,
但其他力做功的代数和为零例1.下列实例(均不计空气阻力)中的运动物体,机械能守恒的是( )
A.被起重机吊起的货物正在加速上升
B.斜抛出去的小球
C.木块沿粗糙斜面匀速下滑
D.光滑水平面上,一个轻质弹簧左端固定,右端连接一小球,沿水平方向做振动的小球 B例2. 忽略一切阻力,如图。摆长为L,最大偏角为θ。小球运动到最低位置时的速度是多大?由机械能守恒定律得即得末状态解:选O所在平面为零势能面初状态 总结:应用机械能守恒定律解题步骤(4)根据机械能守恒定律列出方程,进行求解。(1)确定研究对象和研究过程(2)分析研究对象在运动过程中的受力情况弄清各力做功的情况,判断机械能是否守恒(3) 恰当选取零势能面,并确定研究对象在研究过程的始、末状态的机械能。 【课堂练习】
1.下列实例中的运动物体,哪些机械能不守恒( )
A.跳伞运动员在空中匀速下降
B.滑雪运动员自高坡顶上自由下滑(不计空气阻力和摩擦)
C.汽车在水平路面上匀速行驶
D.集装箱被吊车匀速地吊起(空气阻力不计)AD 2. 如图所示,木块在固定的斜面上运动,其中图C中的斜面是光滑的,图A、B、D中的斜面是粗糙的,图A、B中的F为木块所受的外力,方向如图中箭头所示,大小与摩擦阻力相等,图A、B、D中的木块向下运动,图C中的木块向上运动.在这四个图所示的运动过程中机械能守恒的是( )AC 3、如图所示,轻弹簧下端挂一质量为m的物体,另一端悬挂于O点,现将物体拉到与悬点等高的位置并保持弹簧处于原长状态,放手后物体向下运动.在运动到悬点O正下方的过程中,下列说法正确的是( )
A.物体和地球组成的系统机械能守恒
B.物体和地球组成的系统机械能在减少
C.物体、地球和弹簧三者
组成的系统机械能守恒
D.全过程的初、末状态相比,
重力势能和弹性势能之和增加了C 4.如图所示,轻质弹簧的一端与墙相连,质量为2kg的滑块以5m/s的初速度沿光滑平面运动并压缩弹簧,求:
(1)弹簧在被压缩过程中最大弹性势能.
(2)当木块的速度减为2 m/s时,弹簧具有的弹性势能.(1)由ΔEk= -ΔEp知Ep=25J(2)由EK2-EK1=EP1 -EP2 知
EP2=21J解: 课后拓展
如图所示.一根长L的细绳,固定在O点,绳另一端系一条质量为m的小球.起初将小球拉至水平于A点.求:
(1)小球从A点由静止释放后到达最低点C时的速度。 (2)小球摆到最低点时细绳的拉力。 解:(1)由机械能守恒有:(2) 在最低点,根据牛顿第二定律:解得:有:T-mg=mv2/L解得:T=3mg谢谢!
