《空间几何体的结构》课件
图片预览







文档简介
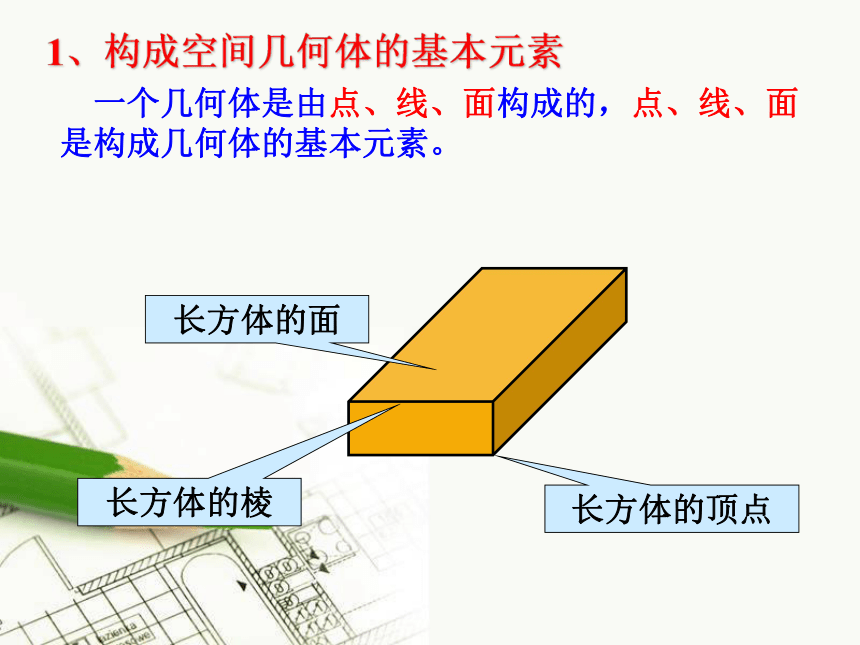
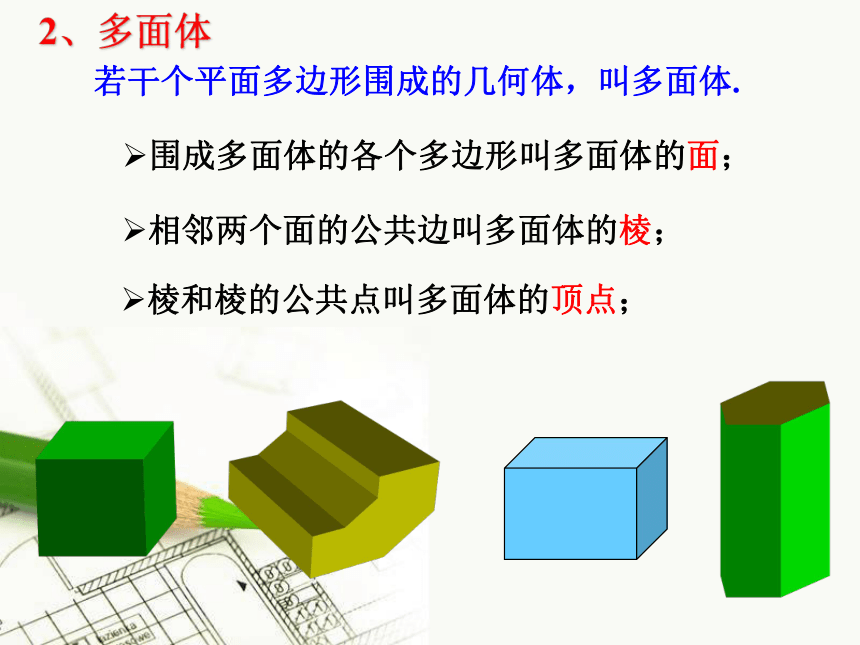
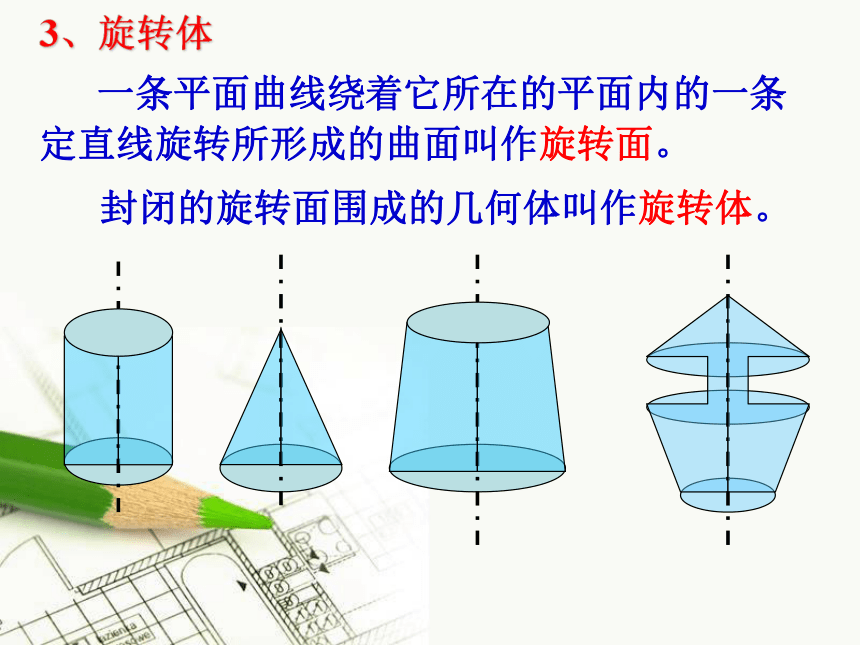
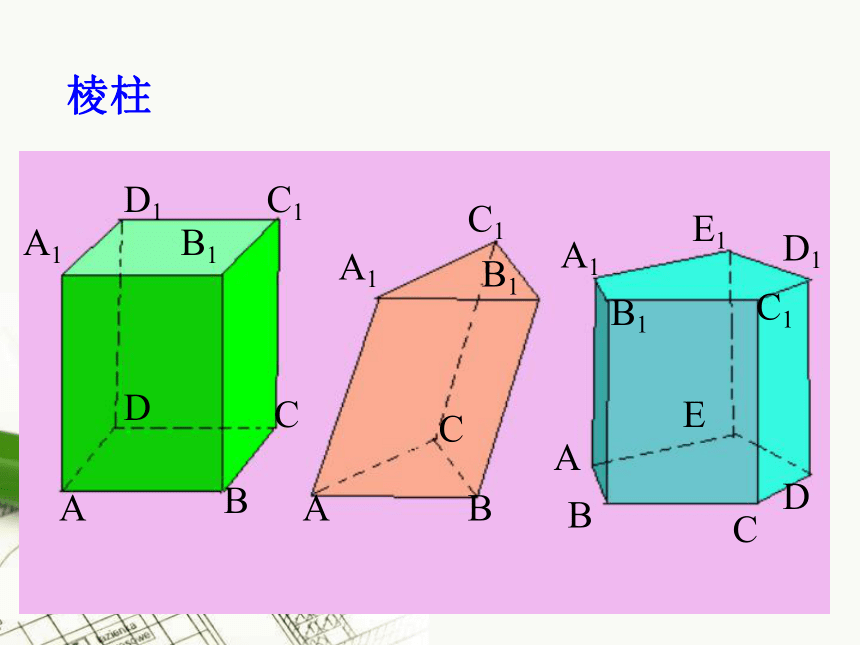
课件56张PPT。1.1空间几何体的结构1、构成空间几何体的基本元素长方体的面长方体的棱长方体的顶点 一个几何体是由点、线、面构成的,点、线、面是构成几何体的基本元素。2、多面体若干个平面多边形围成的几何体,叫多面体.围成多面体的各个多边形叫多面体的面;相邻两个面的公共边叫多面体的棱;棱和棱的公共点叫多面体的顶点;棱柱、棱锥、棱台都是多面体 一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面。封闭的旋转面围成的几何体叫作旋转体。3、旋转体1.1.1 柱、锥、台、球的结构特征ABCDA1A1B1B1C1C1D1ABCA1B1C1D1 E1ABCED棱柱 1、定义:
①有两个面互相平行,
②其余各面都是四边形,
③并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,
其余各叫做棱柱的侧面。相邻侧面的公共边叫做棱柱的侧棱。侧面与底的公共顶点叫做棱柱的顶点。 一、棱柱的结构特征 棱柱(1)有两个面相互平行
(2)其他面都为四边形
(3)相邻四边形的公共边都平行六棱柱直三棱柱斜四棱柱底面侧面侧棱顶点关系平行 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 三棱柱四棱柱五棱柱棱柱的分类1. 侧棱不垂直于底的棱柱叫做斜棱柱。2.侧棱垂直于底的棱柱叫做直棱柱。3. 底面是正多边形的直棱柱叫做正棱柱。3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。4、棱柱的性质(1)侧棱都相等,
侧面是平行四边形;(2)两个底面与平行于底面的截面
是全等的多边形;(3)过不相邻的两条侧棱的截面
是平行四边形。 例1 一个三棱柱可以分割成几个三棱锥?思考:有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?P9 A 1(2)二、棱锥的结构特征观察下列几何体,有什么相同点?1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。 有公共顶点的各个三角形叫做棱锥的侧面。 各侧面的公共顶点叫做棱锥的顶点。 相邻侧面的公共边叫做棱锥的侧棱。棱锥的底面棱锥的侧面棱锥的顶点棱锥的侧棱SABCDEO棱锥(1) 一个面是多边形(2) 其余各面都是有一个公共顶点的三角形三棱锥四棱锥五棱锥(四面体)2、棱锥的分类: 分法:按底面多边形的边数正棱锥 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.正棱锥的基本性质 各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。4.棱锥的性质(1)侧棱相交于一点,侧面是三角形;(3)底面与平行于底面的截面是相似的多
边形。(2)过不相邻的两条侧棱的截面是三角形;三、棱台的结构特征BCADSB1A1C1D1 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1、棱台的概念 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台。下底面上底面侧面侧棱高顶点2、棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…四棱台四棱台三棱台斜高用正棱锥截得的棱台叫作正棱台。正棱台正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。正棱锥正四棱台3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。思考:下列多面体一定是棱台吗?如何判断?注意:棱台的侧棱的延长线必相交于一点例:课本P9 2棱台的性质S棱台的性质(1)侧棱 ,
侧面是 ;延长后交于一点梯形(2)过不相邻的两条侧棱的截面是 ;梯形(3)底面与平行于底面的截面是 。相似的多边形四、圆柱的结构特征矩
形O1O 1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。 (1)旋转轴叫做圆柱的轴。 (2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。 (3)平行于轴的旋转而成的曲面叫做圆柱的侧面。 (4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。2、表示:用表示它的轴的字母表示,
如圆柱OO1。OO13、圆柱与棱柱统称为柱体。五、圆锥的结构特征直角三角形SAO1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。 (1)旋转轴叫做圆锥的轴。 (2) 垂直于轴的边旋转而成的曲面叫做圆锥的底面。 (3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。 (4)无论旋转到什么位置不垂直于轴的边都叫做圆锥的母线。2、圆锥的表示用表示它的轴的字母表示,
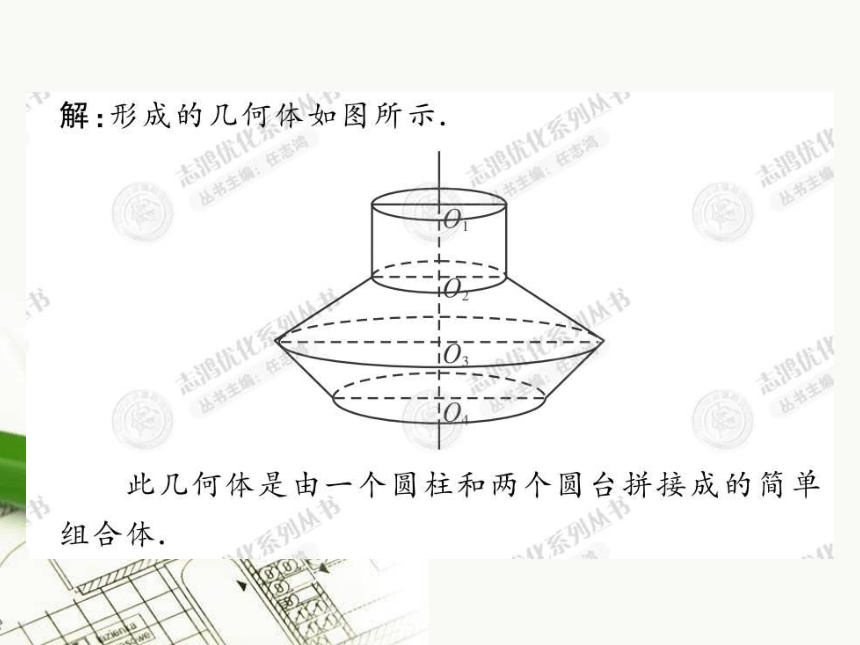
如圆锥SO。3、圆锥与棱锥统称为锥体。六、圆台的结构特征1、定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台。2、圆台的表示:用表示它的轴的字母表示,如圆台OO′3、圆台与棱台统称为台体。③讨论:棱台、圆台分别具有一些什么
几何性质?七、球的结构特征O球心半径AB1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心。(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球心半径直径O球、圆柱、圆锥、圆台过轴的截面分别是什么图形?简单几何体简单旋转体简单多面体球圆
柱圆
锥圆
台棱
柱棱
锥棱
台知识归纳与整理简单几何体柱体锥体台体球棱柱圆柱棱锥圆锥棱台圆台练习:1、下列命题是真命题的是( )A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。A 有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1. 已知圆锥的轴截面等腰三角形的腰长为
5cm, 面积为12cm2,求圆锥的底面半径.
2. 已知圆柱的底面半径为3cm,轴截面面
积为24cm2,求圆柱的母线长.
3. 正四棱锥的底面积为4 cm2,侧面等
腰三角形面积为6cm2,求正四棱锥侧棱.练习
①有两个面互相平行,
②其余各面都是四边形,
③并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,
其余各叫做棱柱的侧面。相邻侧面的公共边叫做棱柱的侧棱。侧面与底的公共顶点叫做棱柱的顶点。 一、棱柱的结构特征 棱柱(1)有两个面相互平行
(2)其他面都为四边形
(3)相邻四边形的公共边都平行六棱柱直三棱柱斜四棱柱底面侧面侧棱顶点关系平行 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 三棱柱四棱柱五棱柱棱柱的分类1. 侧棱不垂直于底的棱柱叫做斜棱柱。2.侧棱垂直于底的棱柱叫做直棱柱。3. 底面是正多边形的直棱柱叫做正棱柱。3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。4、棱柱的性质(1)侧棱都相等,
侧面是平行四边形;(2)两个底面与平行于底面的截面
是全等的多边形;(3)过不相邻的两条侧棱的截面
是平行四边形。 例1 一个三棱柱可以分割成几个三棱锥?思考:有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?P9 A 1(2)二、棱锥的结构特征观察下列几何体,有什么相同点?1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。 有公共顶点的各个三角形叫做棱锥的侧面。 各侧面的公共顶点叫做棱锥的顶点。 相邻侧面的公共边叫做棱锥的侧棱。棱锥的底面棱锥的侧面棱锥的顶点棱锥的侧棱SABCDEO棱锥(1) 一个面是多边形(2) 其余各面都是有一个公共顶点的三角形三棱锥四棱锥五棱锥(四面体)2、棱锥的分类: 分法:按底面多边形的边数正棱锥 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.正棱锥的基本性质 各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。4.棱锥的性质(1)侧棱相交于一点,侧面是三角形;(3)底面与平行于底面的截面是相似的多
边形。(2)过不相邻的两条侧棱的截面是三角形;三、棱台的结构特征BCADSB1A1C1D1 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1、棱台的概念 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台。下底面上底面侧面侧棱高顶点2、棱台的分类:由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…四棱台四棱台三棱台斜高用正棱锥截得的棱台叫作正棱台。正棱台正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。正棱锥正四棱台3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。思考:下列多面体一定是棱台吗?如何判断?注意:棱台的侧棱的延长线必相交于一点例:课本P9 2棱台的性质S棱台的性质(1)侧棱 ,
侧面是 ;延长后交于一点梯形(2)过不相邻的两条侧棱的截面是 ;梯形(3)底面与平行于底面的截面是 。相似的多边形四、圆柱的结构特征矩
形O1O 1、定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。 (1)旋转轴叫做圆柱的轴。 (2) 垂直于轴的边旋转而成的曲面叫做圆柱的底面。 (3)平行于轴的旋转而成的曲面叫做圆柱的侧面。 (4)无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。2、表示:用表示它的轴的字母表示,
如圆柱OO1。OO13、圆柱与棱柱统称为柱体。五、圆锥的结构特征直角三角形SAO1、定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。 (1)旋转轴叫做圆锥的轴。 (2) 垂直于轴的边旋转而成的曲面叫做圆锥的底面。 (3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。 (4)无论旋转到什么位置不垂直于轴的边都叫做圆锥的母线。2、圆锥的表示用表示它的轴的字母表示,
如圆锥SO。3、圆锥与棱锥统称为锥体。六、圆台的结构特征1、定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台。2、圆台的表示:用表示它的轴的字母表示,如圆台OO′3、圆台与棱台统称为台体。③讨论:棱台、圆台分别具有一些什么
几何性质?七、球的结构特征O球心半径AB1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心。(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球心半径直径O球、圆柱、圆锥、圆台过轴的截面分别是什么图形?简单几何体简单旋转体简单多面体球圆
柱圆
锥圆
台棱
柱棱
锥棱
台知识归纳与整理简单几何体柱体锥体台体球棱柱圆柱棱锥圆锥棱台圆台练习:1、下列命题是真命题的是( )A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。A 有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1. 已知圆锥的轴截面等腰三角形的腰长为
5cm, 面积为12cm2,求圆锥的底面半径.
2. 已知圆柱的底面半径为3cm,轴截面面
积为24cm2,求圆柱的母线长.
3. 正四棱锥的底面积为4 cm2,侧面等
腰三角形面积为6cm2,求正四棱锥侧棱.练习
