第9章分式总复习课件

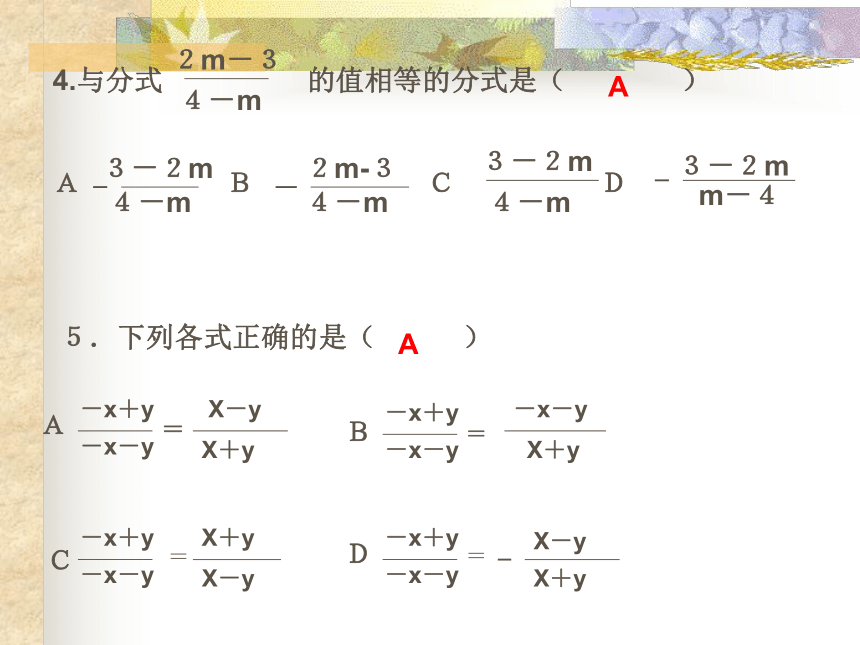
课件47张PPT。分式总复习知识回顾1.分式的定义:2.分式有意义的条件:B≠0分式无意义的条件:B = 03.分式值为 0 的条件:A=0且 B ≠0A>0 ,B>0 或 A<0, B<0A>0 ,B<0 或 A<0 ,B>0练习3Bx ≠-2x≠±1x ≠±1x 为一切实数2x=yX=4X=1X=-3X=1X≠0且x≠-2X=2X>1<-2≥7>-1知识回顾二一个不为0的整式不变B X MB÷M不为0-A-B-BB-AB练习a2+abab+1a2+b2-2ab2a2bCd-c-x-yAABAC5/3知识回顾三
把分母不相同的几个分式化成分母相同的分式。关键是找最简公分母:各分母所有因式的最高次幂的积.1.约分：2.通分:把分子、分母的最大公因式(数)约去。约分与通分的依据都是:分式的基本性质思考题　　两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母。　　分式的乘法法则用符号语言表达：　　两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘。　分式除法法则用符号语言表达：知识回顾一（7）解：注意：
乘法和除法运算时,分子或分母能分解的要分解，结果要化为最简分式 。 分式的加减同分母相加异分母相加通分知识回顾二在分式有关的运算中，一般总是先把分子、分母分解因式；
注意：过程中，分子、分母一般保持分解因式的形式。（6）计算：解：（7）当 x = 200 时，求
的值.解:当 x = 200 时,原式=（8） 已知 求A、B整数指数幂有以下运算性质：知识回顾三4.(2×10-3)2×(2×10-2)-3=　　　　　．2. 0.000000879用科学计数法表示为 .3.如果（2x-1）-4有意义，则 。5.（an+1bm）-2÷anb=a-5b-3，则m= ，n=___.1:下列等式是否正确?为什么?
(1)am÷an= am.a-n; (2)计算2.解分式方程的一般步骤 1、 在方程的两边都乘以最简公分母，约去分母，化成整式方程.
2、解这个整式方程.
3、 把整式方程的根代入最简公分母，看结果是不是为零，使最简公分母为零的根是原方程的增根，必须舍去.
4、写出原方程的根.1.解分式方程的思路是：分式方程整式方程去分母复习回顾一:1、解方程：解：原方程可化为两边都乘以，并整理得；解得检验：x=1是原方程的根，x=2是增根∴原方程的根是x=1例1例2 已知 求A、B解方程：5.若方程 有增根，则增根
应是 　　
6.解关于x的方程
产生增根，则常数a=　　。7、 已知 求A、B列分式方程解应用题的一般步骤1.审:分析题意,找出研究对象，建立等量关系.2.设:选择恰当的未知数,注意单位.3.列:根据等量关系正确列出方程.4.解:认真仔细.5.验:不要忘记检验.6.答:不要忘记写.复习回顾二:例1： 一项工程，需要在规定日期内完成，如果甲队独做，恰好如期完成，如果乙队独做，就要超过规定3天，现在由甲、乙两队合作2天，剩下的由乙队独做，也刚好在规定日期内完成， 问规定日期是几天？解:设规定日期为x天，根据题意列方程请完成下面的过程例2. 已知轮船在静水中每小时行20千米，如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同，那么此江水每小时的流速是多少千米?
　　　解:设江水每小时的流速是x千米，根据题意列方程请完成下面的过程例3.某人骑自行车比步行每小时多走8千米， 如果他步行12千米所用时间与骑车行36千米所用的时间相等，求他步行40千米用多少小时?
解:设他步行1千米用x小时，根据题意列方程请完成下面的过程例4. 甲乙两人分别从相距36千米的A、B两地相向而行，
甲从A出发到1千米时发现有东西遗忘在A地，立即返回，
取过东西后又立即从A向B行进，这样两人恰好在AB中点
处相遇。已知甲比乙每小时多走0.5千米，求二人的速度
各是多少？分析：等量关系 t 甲 = t 乙x18思考题=
1.水池装有两个进水管，单独开甲管需a小时注满空池,单独开乙管需b小时注满空池，若同时打开两管，那么注满空池的时间是（ ）小时
A、 B、 C、 D、学以致用B3.甲加工180个零件所用的时间，乙可以加工240个零件，已知甲每小时比乙少加工5个零件，求两人每小时各加工的零件个数.甲：15
乙：20解：设甲每小时加工x个零件，则乙每小时加工（x+5)个零件，依题意得：=请完成下面的过程