11.3.3一次函数与二元一次方程组[上学期]
文档属性
| 名称 | 11.3.3一次函数与二元一次方程组[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 271.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-09 20:39:00 | ||
图片预览


文档简介
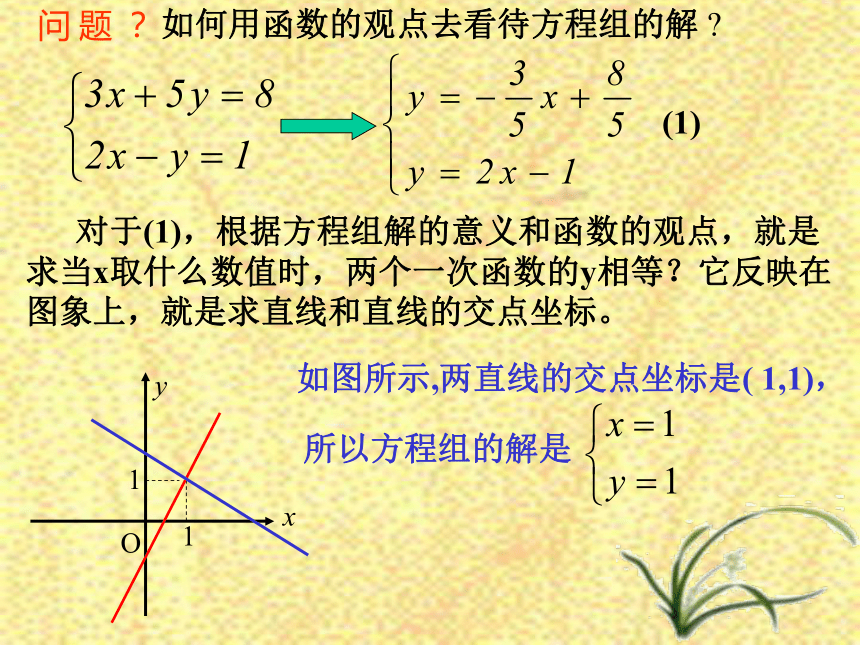
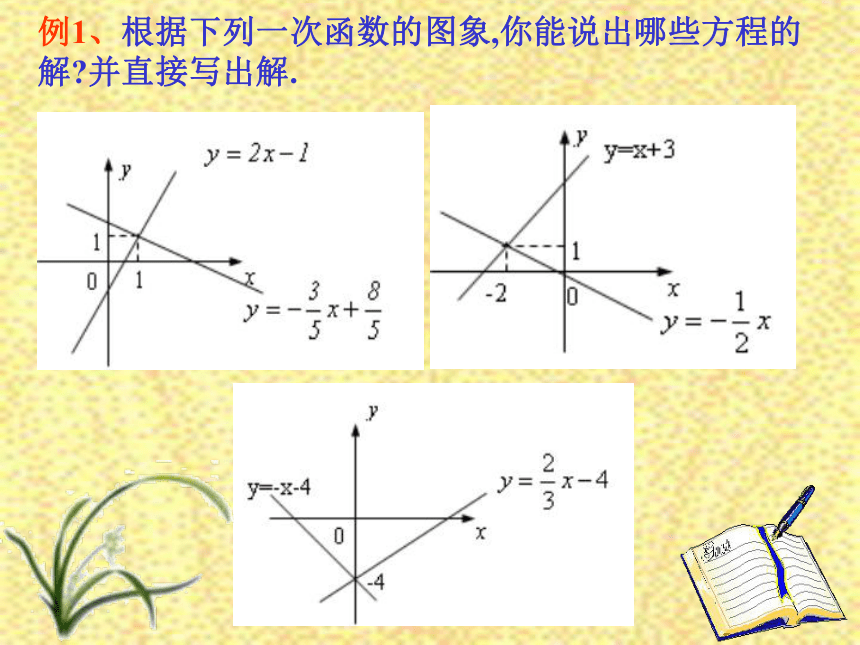
课件9张PPT。11.3 用函数观点看方程(组)与不等式11.3.2 一次函数与二元一次方程组音乐问 题 ?如何用函数的观点去看待方程组的解 ? 对于(1),根据方程组解的意义和函数的观点,就是求当x取什么数值时,两个一次函数的y相等?它反映在图象上,就是求直线和直线的交点坐标。如图所示,两直线的交点坐标是( 1,1), (1)所以方程组的解是例1、根据下列一次函数的图象,你能说出哪些方程的解?并直接写出解.例2、利用函数图象解方程组:
解:由2x-y=0可得:y=2x
由3x+2y=7可得:在同一坐标系内作出一次函数y=2x的图象l1和 的图象l2, 如图所示,得两直线的交点坐标是(1,2)。
所以方程组的解为 练 习1、求函数y=x-1的图象与函数y=-2x+5的图象的交点坐标 :3、求如图所示的两条直线l1, l2的交点坐标。(要求精确的结果) 2、已知直线y=2x+k与直线y=kx-2的交点横坐标为2,求k的值和交点纵坐标。 (1)将两个解析式联列成方程组(2)求出方程组的解(3)写出交点坐标例3、一家电信公司给顾客提供两种上网收费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。如何选择收费方式能使上网者更合算?解法1:设上网时间为x分,若按方式A收y=0.1x元;若按方式B收则收y=0.05x+20元在同一坐标系中分别画出 两函数的图象,解方程组得所以交点坐标是(400,40)因此:当0当x=400时,选择方式A和B没有区别;
当x>400时,选择B方式省钱.例3、一家电信公司给顾客提供两种上网收费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。如何选择收费方式能使上网者更合算?解法2:设上网时间为x分,方式B与方式A两种计费的差额为y元,则y随x变化的函数关系式为y=(0.05x+20)-0.01x化简得:y=-0.05x+20画出这个函数图象解方程0.05x+2=0,得出直线y=-0.05x+20与x轴的交点坐标是(400,0)由函数图象得:当x>400时,y>0,即选择方式B省钱当x=400时,y=0,即选择A、B无区别当x>400时,y<0,即选择方式A省钱答:(略)小 结:1、一次函数与二元一次方程组之间的关系:二元一次方程组的解两个一次函数图象的交点坐标2、图象法解方程组的步骤:(1)将方程组中各方程化为y=ax+b的形式(2)画出每个一次函数的图象(3)由交点坐标得出方程组的解4、方程组、不等式与函数之间互相联系,用函数观点处理时,应根据具体情况灵活、有机地结合起来使用。3、求两个函数的图象的交点:(1)将两个解析式联列成方程组(2)求出方程组的解(3)写出交点坐标
解:由2x-y=0可得:y=2x
由3x+2y=7可得:在同一坐标系内作出一次函数y=2x的图象l1和 的图象l2, 如图所示,得两直线的交点坐标是(1,2)。
所以方程组的解为 练 习1、求函数y=x-1的图象与函数y=-2x+5的图象的交点坐标 :3、求如图所示的两条直线l1, l2的交点坐标。(要求精确的结果) 2、已知直线y=2x+k与直线y=kx-2的交点横坐标为2,求k的值和交点纵坐标。 (1)将两个解析式联列成方程组(2)求出方程组的解(3)写出交点坐标例3、一家电信公司给顾客提供两种上网收费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。如何选择收费方式能使上网者更合算?解法1:设上网时间为x分,若按方式A收y=0.1x元;若按方式B收则收y=0.05x+20元在同一坐标系中分别画出 两函数的图象,解方程组得所以交点坐标是(400,40)因此:当0
当x>400时,选择B方式省钱.例3、一家电信公司给顾客提供两种上网收费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。如何选择收费方式能使上网者更合算?解法2:设上网时间为x分,方式B与方式A两种计费的差额为y元,则y随x变化的函数关系式为y=(0.05x+20)-0.01x化简得:y=-0.05x+20画出这个函数图象解方程0.05x+2=0,得出直线y=-0.05x+20与x轴的交点坐标是(400,0)由函数图象得:当x>400时,y>0,即选择方式B省钱当x=400时,y=0,即选择A、B无区别当x>400时,y<0,即选择方式A省钱答:(略)小 结:1、一次函数与二元一次方程组之间的关系:二元一次方程组的解两个一次函数图象的交点坐标2、图象法解方程组的步骤:(1)将方程组中各方程化为y=ax+b的形式(2)画出每个一次函数的图象(3)由交点坐标得出方程组的解4、方程组、不等式与函数之间互相联系,用函数观点处理时,应根据具体情况灵活、有机地结合起来使用。3、求两个函数的图象的交点:(1)将两个解析式联列成方程组(2)求出方程组的解(3)写出交点坐标
